
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Декартова прямокутна системи координат
|
|
|
|
Проведемо на площині через точку О три взаємно перпендикулярні прямі х, у та z – вісі координат. Вісь х називається віссю абсцис, вісь у – віссю ординат, вісь z – віссю аплікат. Точка перетину О – початком координат.
На віссях координат відмітимо масштаб – одиничний відрізок.
Кожній точці А площини співставимо трійку чисел – координати точки – абсцису (х 0), ординату (у 0), аплікату (z 0). Точки вісі абсцис мають рівні нулю ординати у =0 та аплікати z =0, точки вісі ординат мають рівні нулю абсциси х =0 та аплікати z =0, точки вісі аплікат мають рівні нулю абсциси х =0 та ординати у =0. Початок координат О (0, 0, 0).
Точки площини Оху мають рівні нулю аплікати z =0, точки площини Оуz мають рівні нулю абсциси х =0, точки площини Охz мають рівні нулю ординати у =0.
Вектори  утворюють базис трьохвимірного простору. Їх довжина дорівнює одиниці, тому вони називаються одиничними ортами. Вектор
утворюють базис трьохвимірного простору. Їх довжина дорівнює одиниці, тому вони називаються одиничними ортами. Вектор  паралельний осі абсцис і перпендикулярний площині Оуz. Вектор
паралельний осі абсцис і перпендикулярний площині Оуz. Вектор  паралельний осі ординат і перпендикулярний площині Охz. Вектор
паралельний осі ординат і перпендикулярний площині Охz. Вектор  паралельний осі аплікат і перпендикулярний площині Оху.
паралельний осі аплікат і перпендикулярний площині Оху.
Означення 10.1. Побудовану таким способом систему координат називають декартовою системою координат в просторі.
2. Рівняння площині, їх різновиди.
2.1. Рівняння площини через точку і нормальний вектор.
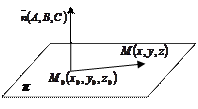 Вектор
Вектор  , перпендикулярний до площини π, називається нормальним або вектор-нормалі.
, перпендикулярний до площини π, називається нормальним або вектор-нормалі.
Нехай пряма проходить через точку  і перпендикулярна вектору
і перпендикулярна вектору  . Візьмемо на площині довільну точку
. Візьмемо на площині довільну точку  . Тоді вектор
. Тоді вектор  . А тому їх скалярний добуток дорівнює нулю.
. А тому їх скалярний добуток дорівнює нулю.
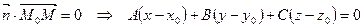 (10.1)
(10.1)
Рівняння 10.1. називається рівнянням площини через точку і нормальний вектор.
2.2. Загальне рівняння площини, її розташування.
|
|
|
В рівнянні 10.1. розкриємо дужки і позначимо вираз  . Отримали рівняння.
. Отримали рівняння.
 (10.2)
(10.2)
Рівняння 10.2. називається загальним рівнянням площини.
Коефіцієнти  є координатами нормального вектора
є координатами нормального вектора  . Причому коефіцієнти
. Причому коефіцієнти  не можуть дорівнювати нулю одночасно.
не можуть дорівнювати нулю одночасно.
2.3. Рівняння площини через точку і два неколінеарні вектори.
Два непаралельні вектори називаються не колінеарними.
Нехай пряма проходить через точку  і два не колінеарні вектори
і два не колінеарні вектори 
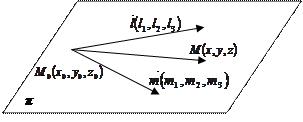 ,
,  ,
,  . Візьмемо на площині довільну точку
. Візьмемо на площині довільну точку  . Тоді вектор
. Тоді вектор  можна розкласти за векторами
можна розкласти за векторами 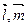 . А тому вектор
. А тому вектор  є лінійною комбінацією векторів
є лінійною комбінацією векторів 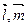 :
:  , з чого випливає, що вектори
, з чого випливає, що вектори  – лінійно залежні, а отже визначник складений з координат векторів повинен дорівнювати нулю.
– лінійно залежні, а отже визначник складений з координат векторів повинен дорівнювати нулю.
 (10.3)
(10.3)
Рівняння 10.3. називається рівнянням площини через точку і два неколінеарні вектори.
2.4. Рівняння площини через три не колінеарні точки.
Точки, що лежать на одній прямій називаються колінеарними.
 Нехай площина проходить через не колінеарні точки
Нехай площина проходить через не колінеарні точки 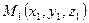 ,
, 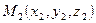 і
і  . В якості векторів
. В якості векторів 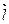 ,
,  візьмемо вектори
візьмемо вектори  ,
,  , які є неколінеарними. Підставивши в рівняння 10.3., отримаємо:
, які є неколінеарними. Підставивши в рівняння 10.3., отримаємо:
 (10.4)
(10.4)
Рівняння 10.4. називається рівнянням площини через три не колінеарні точки.
2.5. Рівняння площини у відрізках.
 Нехай площина перетинає вісь абсцис в точці
Нехай площина перетинає вісь абсцис в точці  , вісь ординат в точці
, вісь ординат в точці  , вісь аплікат в точці
, вісь аплікат в точці  . Ці точки не колінеарні. Запишемо рівняння площини через три точки 10.4.
. Ці точки не колінеарні. Запишемо рівняння площини через три точки 10.4.
 ;
;
 ;
;
 ;
;  ;
;
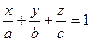 (10.5)
(10.5)
Рівняння 10.5. називається рівнянням площини у відрізках.
2.6. Розташування площини відносно системи координат.
З’ясуємо як розташовується площина  відносно осей координат.
відносно осей координат.
1. Нехай  . Тоді
. Тоді  , вектор нормалі
, вектор нормалі  , бо
, бо 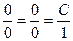 .
. 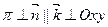 , тому
, тому  .
.
2. Нехай 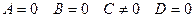 . Тоді
. Тоді  ,
,  , тому
, тому  .
.
3. Нехай  . Тоді
. Тоді  , вектор нормалі
, вектор нормалі  , бо
, бо  .
.  , тому
, тому  .
.
4. Нехай  . Тоді
. Тоді  ,
,  , тому
, тому 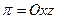 .
.
5. Нехай  . Тоді
. Тоді  , вектор нормалі
, вектор нормалі 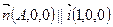 , бо
, бо  .
.  , тому
, тому  .
.
6. Нехай 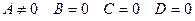 . Тоді
. Тоді  ,
, 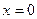 , тому
, тому 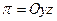 .
.
7. Нехай  . Тоді
. Тоді  , вектор нормалі
, вектор нормалі  , бо
, бо 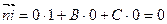 .
.  , тому
, тому  .
.
8. Нехай 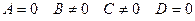 . Тоді
. Тоді  .
.  ,
,  , тому
, тому  .
.
9. Нехай  . Тоді
. Тоді 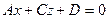 , вектор нормалі
, вектор нормалі  , бо
, бо  .
. 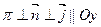 , тому
, тому  .
.
10. Нехай  . Тоді
. Тоді  .
.  ,
,  , тому
, тому  .
.
11. Нехай  . Тоді
. Тоді  , вектор нормалі
, вектор нормалі  , бо
, бо  .
.  , тому
, тому  .
.
|
|
|
12. Нехай  . Тоді
. Тоді  .
.  ,
, 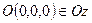 , тому
, тому  .
.
13. Нехай  . Тоді
. Тоді  .
.  , площина проходить через початок координат.
, площина проходить через початок координат.
3. Умови паралельності та перпендикулярності площин. Відстань від точки до площини.
3.1. Умова паралельності площин.
Нехай площини задані в загальному вигляді  та
та  .
.
 (10.6)
(10.6)
Дві площини паралельні тоді і тільки тоді, коли відповідні коефіцієнти при змінних х, у, z пропорційні.
3.2. Умова перпендикулярності площин.
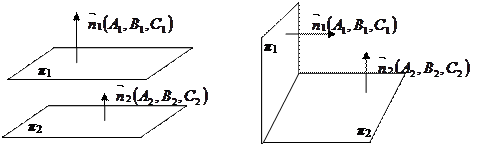
Нехай площини задані в загальному вигляді  та
та  .
.
 (10.7)
(10.7)
Дві площини перпендикулярні тоді і тільки тоді, коли сума добутків відповідних коефіцієнти при змінних х, у, z дорівнює нулю.
3.3. Відстань від точки до площини.
Означення 10.2. Довжина перпендикуляра, проведеного з точки на площину називається відстанню від цієї точки до площини. Якщо точка належить площині, то відстань дорівнює нулю.
Нехай задані площина в загальному вигляді  і точка
і точка  . Відстань від точки до площини знаходиться аналогічно як відстань від точки до прямої. В результаті отримаємо:
. Відстань від точки до площини знаходиться аналогічно як відстань від точки до прямої. В результаті отримаємо:
 (10.8)
(10.8)
3.4. Відстань між двома паралельними площинами.
Нехай площини задані в загальному вигляді  та
та  .
.
Візьмемо точку  на площині
на площині  .
.  .
.  . Підставимо в 10.8
. Підставимо в 10.8
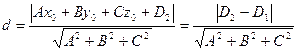 (10.9)
(10.9)
3.5. Кут між двома площинами.
Нехай площини задані в загальному вигляді  та
та  .
. 

 (10.10)
(10.10)
4. Рівняння прямої в просторі, їх різновиди.
4.1. Рівняння прямої як перетин двох площин.
Нехай площини задані в загальному вигляді  та
та  . З курсу стереометрії відомо що, якщо дві площини мають спільну точку, то вони перетинаються по прямій. Іншими словами довільні дві непаралельні площини задають пряму. Тобто якщо
. З курсу стереометрії відомо що, якщо дві площини мають спільну точку, то вони перетинаються по прямій. Іншими словами довільні дві непаралельні площини задають пряму. Тобто якщо  (не виконується умова паралельності), то
(не виконується умова паралельності), то
 (11.1)
(11.1)
Рівняння 11.1. називається рівнянням прямої як перетин двох площин.
4.2. Канонічне рівняння прямої.
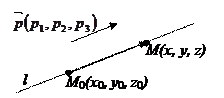 Нехай пряма проходить через точку
Нехай пряма проходить через точку  і паралельна вектору
і паралельна вектору  . Візьмемо на прямій довільну точку
. Візьмемо на прямій довільну точку  . Тоді вектор
. Тоді вектор  . А тому координати векторів повинні бути пропорційними.
. А тому координати векторів повинні бути пропорційними.
 (11.2)
(11.2)
Рівняння 11.2. називається рівнянням прямої через точку і напрямний вектор або канонічним рівнянням прямої.
4.3. Рівняння прямої через дві точки.
 Нехай пряма проходить через точки
Нехай пряма проходить через точки 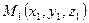 і
і 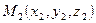 . В якості вектора
. В якості вектора  візьмемо вектор
візьмемо вектор  , який паралельний прямій l, а тому і вектору
, який паралельний прямій l, а тому і вектору  . Підставивши в рівняння 11.2., отримаємо:
. Підставивши в рівняння 11.2., отримаємо:
|
|
|
 (11.3)
(11.3)
Рівняння 11.3. називається рівнянням прямої через дві точки.
4.4. Параметричне рівняння прямої.
Нехай пряма l задається рівнянням 11.2. Введемо параметр t наступним чином  . Тоді прирівнявши кожен дріб, маємо систему:
. Тоді прирівнявши кожен дріб, маємо систему:
 (11.4)
(11.4)
Рівняння 11.4. називається параметричним рівнянням прямої.
4.5. Розташування прямої відносно системи координат.
З’ясуємо як розташовується пряма  відносно осей координат.
відносно осей координат.
1. Нехай  . Тоді напрямний вектор
. Тоді напрямний вектор  , бо
, бо 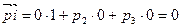 . Тому
. Тому 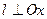 . А оскільки
. А оскільки  , то
, то  .
.
2. Нехай 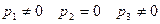 . Тоді напрямний вектор
. Тоді напрямний вектор 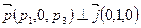 , бо
, бо  . Тому
. Тому  . А оскільки
. А оскільки  , то
, то 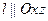 .
.
3. Нехай  . Тоді напрямний вектор
. Тоді напрямний вектор  , бо
, бо  . Тому
. Тому  . А оскільки
. А оскільки  , то
, то  .
.
4. Нехай  .
.  ,
,  , тоді
, тоді  (пряма, що паралельна двом площинам, паралельна і прямій, по якій вони перетинаються). Або це доводиться так: напрямний вектор
(пряма, що паралельна двом площинам, паралельна і прямій, по якій вони перетинаються). Або це доводиться так: напрямний вектор 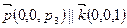 , бо
, бо  , тому
, тому  .
.
5. Нехай  .
.  ,
,  , тоді
, тоді  . Або напрямний вектор
. Або напрямний вектор  , бо
, бо  , тому
, тому  .
.
6. Нехай 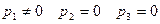 .
.  ,
,  , тоді
, тоді  . Або напрямний вектор
. Або напрямний вектор  , бо
, бо  , тому
, тому  .
.
5. Взаємне розташування двох прямих в просторі.
Розкрити зміст поняття «взаємне розташування прямих в просторі». Розкрити порядок визначення взаємного положення прямих в просторі, ґрунтуючись на означенні кута між двома векторами. Приклади.
 Нехай є дві прямі
Нехай є дві прямі 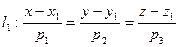 і
і  . У просторі дві прямі можуть бути мимобіжними, паралельними, перетинатися, співпадати.
. У просторі дві прямі можуть бути мимобіжними, паралельними, перетинатися, співпадати.
1. Мимобіжні прямі. Це можливо тоді, коли вектори  ,
,  ,
,  не можуть лежати в одній площині, тобто вони – лінійно незалежні, а отже визначник складений з координат векторів повинен дорівнювати нулю.
не можуть лежати в одній площині, тобто вони – лінійно незалежні, а отже визначник складений з координат векторів повинен дорівнювати нулю.
 (11.5)
(11.5)
2. Прямі, що перетинаються. Це можливо тоді, коли вектори  ,
,  ,
,  лежать в одній площині, але
лежать в одній площині, але  . Тоді вектор
. Тоді вектор  можна розкласти за векторами
можна розкласти за векторами 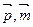 . А тому вектор
. А тому вектор  є лінійною комбінацією векторів
є лінійною комбінацією векторів 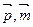 :
:  , з чого випливає, що вектори
, з чого випливає, що вектори  – лінійно залежні, а отже визначник складений з координат векторів повинен дорівнювати нулю.
– лінійно залежні, а отже визначник складений з координат векторів повинен дорівнювати нулю.
 (11.6)
(11.6)
3. Паралельні прямі. Це можливо тоді, коли вектори  ,
,  паралельні між собою, але не паралельні вектору
паралельні між собою, але не паралельні вектору  .
.
 (11.7)
(11.7)
3. Прямі, що співпадають. Це можливо тоді, коли вектори  ,
,  ,
,  паралельні між собою.
паралельні між собою.
 (11.8)
(11.8)
6. Взаємне розташування прямої та площини в просторі.
 |
Розкрити порядок визначення взаємного положення прямої та площини в просторі, ґрунтуючись на означенні кута між двома векторами. Приклади.
|
|
|
Нехай є пряма  і площина
і площина  . У просторі пряма може перетинати площину, бути паралельною площині, або належати площині.
. У просторі пряма може перетинати площину, бути паралельною площині, або належати площині.
1. Перетин прямої і площини. Це можливо тоді, коли вектори  ,
,  не є перпендикулярними, тобто скалярний добуток векторів не дорівнює нулю.
не є перпендикулярними, тобто скалярний добуток векторів не дорівнює нулю.
 (11.9)
(11.9)
2. Паралельність прямої і площини. Це можливо тоді, коли вектори  ,
,  є перпендикулярними, тобто скалярний добуток векторів дорівнює нулю. Але жодна точка прямої не належить площині, тобто точка
є перпендикулярними, тобто скалярний добуток векторів дорівнює нулю. Але жодна точка прямої не належить площині, тобто точка  не задовольняє рівняння площини.
не задовольняє рівняння площини.
 (11.10)
(11.10)
3. Пряма належить площині. Це можливо тоді, коли вектори  ,
,  є перпендикулярними, тобто скалярний добуток векторів дорівнює нулю. Та всі точки прямої належать площині, тобто точка
є перпендикулярними, тобто скалярний добуток векторів дорівнює нулю. Та всі точки прямої належать площині, тобто точка  задовольняє рівняння площини.
задовольняє рівняння площини.
 (11.11)
(11.11)
7. Кут між двома прямими.
Нехай є дві прямі 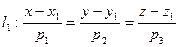 і
і  .
.

 (11.12)
(11.12)
8. Кут між прямою та площиною.
 Нехай є пряма
Нехай є пряма  і площина
і площина  .
.


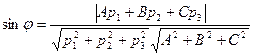 (11.13)
(11.13)
|
|
|
|
Дата добавления: 2014-12-23; Просмотров: 1049; Нарушение авторских прав?; Мы поможем в написании вашей работы!