Формула Ньютона-Лейбниця

Задача про шлях.

Нехай протягом часу вздовж осі рухається точка від точки О зі мінною швидкістю 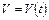, де t – час, V – швидкість. Розіб’ємо відрізок ОТ на п частин довільним чином: . На кожному проміжку візьмемо довільний фіксований момент часу 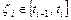(зета). Обчислимо швидкості точки в ці моменти часу: .

Припустимо, що на кожному проміжку часу 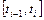точка рухається рівномірно, зі сталою швидкістю . Тоді пройдений час точкою за цей проміжок часу буде дорівнюватиме . За весь час Т точка пройде шлях – це наближене значення шляху, що залежить від розбиття та від вибору точок.

Результат буде точніше, якщо проміжки часу зменшувати, тому за означенням шлях, пройдений точкою за час Т, дорівнює .

1.2. Задача про площу криволінійної трапеції.

Нехай на відрізку 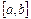визначена невід’ємна функція 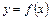. Розіб’ємо відрізок ab на п частин довільним чином: 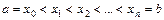. На кожному проміжку візьмемо довільну фіксовану точку 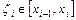(зета). Обчислимо значення функції в цих точках: .

Припустимо, що на кожному проміжку часу 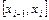крива паралельна вісі Ох. Утворилися прямокутники. Площа прямокутника зі сторонами 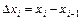і дорівнюватиме 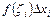. Вся площа під кривою 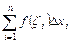– це наближене значення площі, що залежить від розбиття та від вибору точок.

Результат буде точніше, якщо проміжки зменшувати, тому .

2. Визначений інтеграл.

Нехай на відрізку 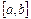визначена функція 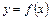. Розіб’ємо відрізок ab на п частин довільним чином: 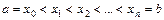. На кожному проміжку візьмемо довільну фіксовану точку 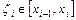(зета). Обчислимо значення функції в цих точках: .

Сума 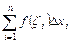називається інтегральною сумою для функції.

Означення 3.1. Нехай границя інтегральної суми при прямуванні існує, скінчений та не залежить від розбиття та від вибору точок. Тоді ця границя називається визначеним інтегралом від функції на 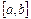і позначається 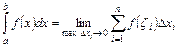, де ∫ – знак інтеграла, – підінтегральна функція, – підінтегральний вираз, а – нижня межа, b – верхня межа.

Зауваження. Невизначений інтеграл – це множина функцій, а визначений інтеграл – це число.

Теорема 3.1 (І необхідна умова існування означеного інтеграла). Для того, щоб функція 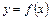була інтегрована на сегменті 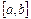необхідно, щоб ця функція була обмежена на цьому сегменті.

Теорема 3.2 (І достатня умова існування означеного інтеграла). Якщо функція 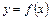неперервна на сегменті 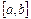, то вона інтегрована на цьому сегменті.

Теорема 3.3 (ІІ достатня умова існування означеного інтеграла). Якщо функція 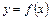обмежена і монотонна на сегменті 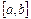, то вона інтегрована на цьому сегменті.

Геометричний зміст визначного інтеграла. Якщо 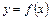– невід’ємна функція на відрізку 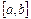, то –площа криволінійної трапеції під кривою 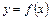на відрізку .

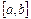3. Властивості визначеного інтеграла.

Властивість 1. .

Властивість 2. .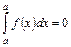

Властивість 3. Сталий множник можна винести за знак інтеграла.

.

Властивість 4. Інтеграл суми дорівнює сумі інтегралів.

.

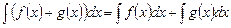Властивість 5. Якщо відрізок інтегрування розбити на частини, то інтеграл на всьому відрізку дорівнює сумі інтегралів на кожній його частині.

.

Властивість 6. Якщо на відрізку 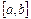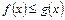, то .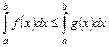

Властивість 7. .

Властивість 8. Якщо функція 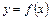неперервна на сегменті 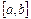, то знайдеться таке значення 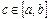, що .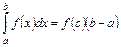

Означення 3.2. Інтеграл 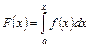називається інтегралом із змінною верхньою межею.

Властивість 9. Якщо функція 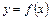неперервна на сегменті 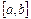, то функція 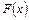також неперервна на сегменті .

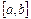Властивість 10. Якщо функція 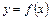неперервна на сегменті 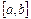, то похідна від функції 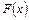по змінній верхній межі дорівнює підінтегральній функції.

.

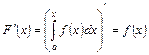Теорема. Нехай функція 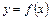неперервна на сегменті 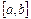, 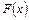– довільна первісна на 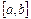. Тоді визначений інтеграл від функції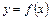 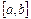дорівнює приросту первісної на цьому відрізку.

.

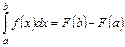Приклад 3.1. .

5. Метод заміни змінної.

Теорема. Нехай функція має неперервну похідну на сегменті , , 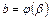і функція , неперервна в кожній точці х виду , де . Тоді має місце формула заміни змінної.

.

Дата добавления: 2014-12-24