
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лабораторная работа № 10
Тема: «Исследование на экстремум таблично заданной функции с использованием интерполирования сплайнами»
Напомним, что сплайн – это функция, которая на каждом частичном отрезке интерполяции является алгебраическим многочленом, а на всем заданном отрезке непрерывна вместе с несколькими своими производными.
Наиболее распространенными на практике являются кубические сплайны или сплайны третьей степени. Для простоты и наглядности последующих преобразований, а также для лучшего понимания алгоритма построения сплайнов, рассмотрим ниже алгоритм для квадратичных сплайнов.
Пусть интерполируемая функция 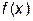 задана своими значениями
задана своими значениями 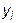 в узлах
в узлах 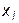 ,
,  . Длину частичного отрезка
. Длину частичного отрезка 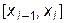 обозначим
обозначим 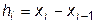 .
.
Будем строить квадратичный сплайн на каждом из частичных отрезков 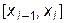 в виде
в виде
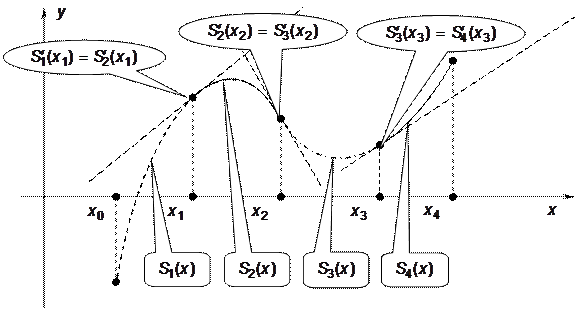
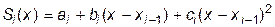 , (10.1)
, (10.1)
где 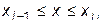 и
и 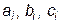 – тройка неизвестных коэффициентов, а всего их будет ровно
– тройка неизвестных коэффициентов, а всего их будет ровно 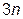 .
.
Итак, каждый квадратичный сплайн 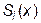 характеризуется пятью параметрами:
характеризуется пятью параметрами: 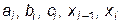 .
.
Для определения неизвестных коэффициентов 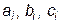 нам предстоит составить систему из
нам предстоит составить систему из 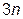 алгебраических уравнений.
алгебраических уравнений.
Обязательное требование совпадения значений в узлах интерполирования у табличной функции и соответствующего сплайна даст нам 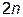 уравнений. Причем совпадение указанных значений в «левых» узлах
уравнений. Причем совпадение указанных значений в «левых» узлах 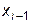 интервалов интерполирования
интервалов интерполирования 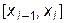 дает сразу значения для всех коэффициентов
дает сразу значения для всех коэффициентов 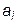 , т.е.
, т.е.
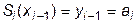 ,
,  . (10.2)
. (10.2)
Тогда для «правых» узлов будет:
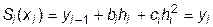 ,
,  . (10.3)
. (10.3)
Для определения оставшихся коэффициентов нам требуется еще 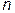 уравнений. Следуя идее сплайн-интерполирования, потребуем совпадения значения первых производных для смежных сплайнов
уравнений. Следуя идее сплайн-интерполирования, потребуем совпадения значения первых производных для смежных сплайнов 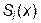 и
и 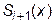 во внутренних узлах интерполяции:
во внутренних узлах интерполяции:
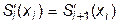 , что дает
, что дает 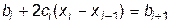 ,
, 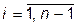 . (10.4)
. (10.4)
Поскольку в таблице исходных данных внутренних узлов имеется всего 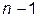 , то нам потребуется еще одно дополнительное условие.
, то нам потребуется еще одно дополнительное условие.
Остановимся подробнее на этом моменте. Классический подход заключается в том, что принимаются дополнительные допущения к поведению сплайнов на концах общего интервала интерполирования.
Например, для кубических сплайнов принимается, что в точках 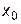 и
и 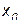 вторые производные соответствующих сплайнов равны нулю, т.е.
вторые производные соответствующих сплайнов равны нулю, т.е. 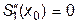 и
и 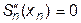 . Геометрически это означает, что указанные кубические сплайны в граничных узлах
. Геометрически это означает, что указанные кубические сплайны в граничных узлах 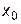 и
и 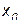 имеют точки перегиба.
имеют точки перегиба.
Данное требование не может быть непосредственно перенесено на случай квадратичных сплайнов, поскольку равенство нулю второй производной для таких функций автоматически значит понижение степени многочлена. Поэтому мы должны воспользоваться каким-то иным допущением.
Например, мы можем построить первый квадратичный сплайн 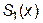 , предполагая, что эта функция проходит через первые три точки из таблицы интерполирования. Другими словами, мы потребуем выполнения следующего дополнительного условия
, предполагая, что эта функция проходит через первые три точки из таблицы интерполирования. Другими словами, мы потребуем выполнения следующего дополнительного условия
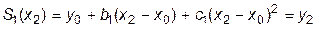 . (10.5)
. (10.5)
В итоге, система линейных алгебраических уравнений (10.3)–(10.5) совместна (количество уравнений равно числу неизвестных) и мы ее можем решать, например, при помощи уже разработанного нами ранее метода Гаусса (лабораторная работа № 5).
Для удобства программирования матрицы коэффициентов системы (10.3)–(10.5) скомпонуем ее уравнения в следующем порядке:
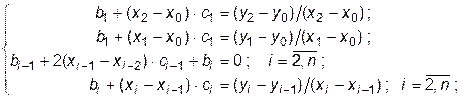 (10.6)
(10.6)
или с учетом обозначения 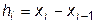 :
:
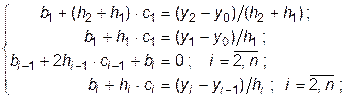 (10.7)
(10.7)
и представим ее в виде следующей диаграммы:
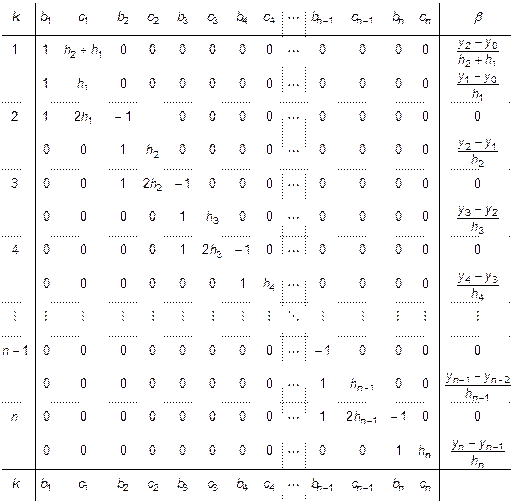 (10.8)
(10.8)
Каждые две последовательные строки диаграммы (10.8) соответствуют квадратичному сплайну, номер которого вынесен слева от этих строк. Столбец 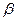 – столбец свободных членов системы (10.3)–(10.5). Размер полученной матрицы
– столбец свободных членов системы (10.3)–(10.5). Размер полученной матрицы 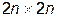 , где
, где 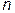 – количество интервалов интерполирования (количество сплайнов).
– количество интервалов интерполирования (количество сплайнов).
|
|
Дата добавления: 2014-12-24; Просмотров: 407; Нарушение авторских прав?; Мы поможем в написании вашей работы!