Тема 4. Математическое программирование 2 страница

Поскольку симплекс-таблица является полуприведенной, то по крайней мере среди коэффициентов целевой функции (исключая ее свободный член 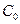) имеется хотя бы один отрицательный. Выберем любой из этих коэффициентов. Столбец, в котором находится выбранный отрицательный коэффициент целевой функции следует принять за разрешающий столбец. Разрешающий элемент в этом столбце выбирается точно так же, как в предыдущем правиле.

Пример. В качестве примера применения симплекс-метода найдем решение сформулированной выше задачи (1.4) – (1.6).

Решение. Задача (1.4) – (1.6) должна быть записана в виде (1.7) – (1.9); согласно (1.10) введены дополнительные неотрицательные переменные и составлена исходная симплекс-таблица (1.11) задачи.

Очевидно, что симплекс-таблица является полуприведенной, поскольку её столбец свободных членов не содержит отрицательных членов. Согласно изложенному выше, для получения оптимального решения симплекс-таблицу (1.11) рассматриваемой задачи необходимо преобразить к приведенному состоянию. Для этого требуется выбрать разрешающий элемент преобразования в соответствии с правилом выбора разрешающего элемента для нахождения оптимального решения.

В симплекс-таблице (1.11) два коэффициента целевой функции отрицательны. Следовательно, любой из столбцов этой таблицы, в которых находятся отрицательные коэффициенты целевой функции – первый или второй – может быть выбран в качестве разрешающего. Примем в качестве разрешающего первый столбец и для наглядности выделим его. Теперь выберем в разрешающем столбце разрешающий элемент в соответствии с выше изложенным правилом, состоящем в следующем. Составим все отрицательные отношения свободных членов симплекс-таблицы (1.11) (исключая свободный член 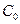целевой функции) к элементам разрешающего столбца и определим их максимум:

Элемент 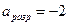первой строки разрешающего столбца, для которого отношение к нему свободного члена максимально, выберем в качестве разрешающего.

Таким образом, выбраны разрешающий столбец, разрешающий элемент в нем и, следовательно, разрешающая строка. Для наглядности выделим из в симплекс-таблице (1.11).

В соответствии с выбором разрешающего элемента 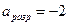, следует выполнить симплекс-преобразование , т.е. свободное переменное 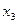перевести в свободные. Выполним эту процедуру в соответствии с изложенным выше алгоритмом симплекс - преобразований. Предварительно составим новую симплекс-таблицу, в которой необходимо поменять местами переменные и 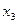. Выполним расчет элементов новой симплекс-таблицы.

Условимся символом (i, j) обозначать содержимое клетки симплекс-таблицы, расположенной в i-ой строке и j-ом столбце этой таблице.

1. Разрешающий элемент 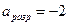заменим его обратной величиной и запишем в клетку (1, 2) новой симплекс-таблицы.

2. Элементы разрешающего (т.е. первого) столбца делим на разрешающий элемент (-2) и результаты записываем в соответствующие клетки первого столбца новой симплекс-таблицы.

3. У элементов разрешающей (т.е. первой) строки меняет знаки и делим из на разрешающий элемент (-2). Результаты записываем в соответствующие клетки первой строки новой симплекс-таблицы.

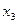
			св. чл.
	-1/2	-1/2
		-1
	½	-3/2
	3/2	-1/2	-45

4. Значения всех остальных элементов исходной симплекс-таблицы (1.11) (не принадлежащих ни разрешающему столбцу, ни разрешающей строки) пересчитываются по «правилу прямоугольников» и записываются в соответствующие клетки новой симплекс-таблицы:

Таким образом, в результате выполненного симплекс - преобразования получена новая симплекс-таблица (1.12):

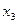
			сл. чл.
	-1/2	-1/2
		-1
	½	-3/2
	3/2	-1/2	-45

(1.12)

Полученная симплекс-таблица (1.12) также является полуприведенной, поскольку целевая функция имеет один отрицательный коэффициент. Поэтому необходимо еще раз выполнить надлежащее симплекс – преобразование, приближающее к искомому оптимальному решению задачи, которое согласно теореме 2 достигается при приведенном состоянии симплекс-таблицы.

Согласно правилу выбора разрешающего элемента для нахождения оптимального решения разрешающим столбцом в симплекс-таблице (1.12) является второй столбец. Составим все отрицательные отношения свободных членов симплекс-таблицы (1.12) к элементам разрешающего столбца (исключая свободный член 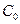целевой функции) и определим их максимум:

Элемент второй строки разрешающего столбца, для которого отношение к нему свободного члена максимально, выберем в качестве разрешающего.

Таким образом, выбраны разрешающий столбец, разрешающий элемент в нем и, следовательно, разрешающая строка. Для наглядности выделим их в симплекс-таблице (1.12).

Составим новую симплекс-таблицу (1.13) и вычислим её элементы в соответствие с выше изложенным алгоритмом симплекс – преобразований. Получим:

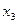
			св. чл.
		½
	-1
	-1	3/2
	1/6	½	-50

Симплекс-таблица (1.13) является приведенной в ней все свободные члены и все коэффициенты целевой функции неотрицательны (за исключением коэффициента целевой функции). Согласно теореме 2 этому (приведенному) состоянию симплекс-таблицы отвечает искомое оптимальное решение задачи. Согласно теореме 3, если оптимальное решение задачи линейного программирования существует, то оно является опорным, т.е. решением в котором согласно определению опорного решения все свободные переменные (в симплекс-таблице (1.13) это 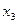и ) равны нулю. Полагая из (1.13) получаем: Эти значения берем из столбца свободных членов. Если то Таким образом, при решении задачи симплекс-методом получены те же результаты, которые нам уже известны в результате рассмотренного выше графического метода решения.

Ответ. План производства таков: предприятие должно производить 10 изделий вида А и 10 изделий вида В. При их полной реализации предприятие получит максимальную прибыль в размере 50 денежных единиц.

Задача 2

Имеются три пункта отправления однородного груза и пять пунктов его назначения. На пунктах груз находится в количестве тонн соответственно. В пункты требует доставить соответственно тонн груза. Расстояния в сотнях километров между пунктами отправления и назначения приведены в матрице D:

Пункты отправления	Пункты назначения

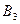
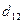
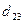
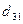
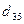
Найти такой план перевозок, при котором общие затраты на перевозку грузов будут минимальными.

Указания: 1) считать стоимость перевозок пропорционой количеству груза и расстоянию, на которое груз перевозится, т.е. для решения задачи достаточно минимизировать общий объем плана, выраженный в тонно-километрах; 2) для решения задачи использовать методы северо-западного угла и потенциалов.

1. Транспортная задача линейного программирования

Рассматриваемая задача о перевозках грузов является так называемой транспортно задачей линейного программирования.

Пусть имеется т пунктов отправления 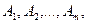в которых находятся некоторые однородные грузы в количестве соответственно 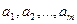единиц. Все грузы из всех пунктов отправления нужно доставить в п пунктов назначения в количестве соответственно. Известна стоимость перевозки единицы груза из каждого пункта отправления 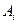в каждый пункт назначения .

Требуется составить план перевозок, при котором все грузы из пунктов отправления будут вывезены, все потребности пунктов назначения будут полностью удовлетворены и при том общая стоимость всех перевозок была бы минимальной.

Составим математическую модель задачи.

Обозначим через количество единиц груза, запланированных к перевозке из i- го пункта отправления в j- ый пункт назначения.

Так как общий запас груза, отправляемого из i- го пункта, равен , то должны выполняться соотношения :

(2.1)

Общее количество груза, доставленного в j- ый пункт со всех пунктов отправления, равно в j; поэтому должны выполняться условия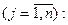

(2.2)

Так как i- го пункта отправления в j- ый пункт назначения запланировано к перевозке единицу груза, то стоимость такой перевозки составит 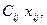а общая стоимость всех перевозок составит

(2.3)

Таким образом, математическая модель транспортной задачи имеет следующий вид:

Найти наименьшее значение линейной функции при ограничениях

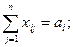
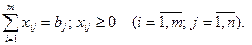
В рассмотренной модели предполагается, что суммарные запасы груза в пунктах отправления равны суммарным потребностям в пунктах назначения, т.е.

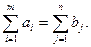(2.4)

Модель транспортной задачи, удовлетворяющей условию (2.4) называется закрытой. Любая транспортная задача, для которой выполняется условие (2.4), имеет решение.

Система ограничений (2.1) и (2.2) транспортной задачи содержит неизвестных и уравнений, связанных соотношением (2.4) (балансным условием). Складывая между собой все уравнения (2.1) и все уравнения (2.3), получаем условие (2.4). Таким образом, условия (2.1) и (2.2) связаны одной линейной зависимостью и, следовательно, система ограничений транспортной задачи содержит не , а только линейно независимых уравнений, т.е. ранг этой системы на единицу меньше числа ее уравнений:

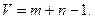
Следовательно, можно разрешить эти уравнения относительно базисных переменных, выразив их через остальные, свободные переменные. Количество свободных переменных равно

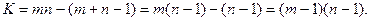
При решении транспортной задачи используются следующие понятия и определения.

Значения количества единиц груза, которое нужно доставить из i- го пункта отправления в j- ый пункт назначения называют перевозкой

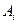Матрицу размера каждый элемент которой означает перевозку из пункта отправления в пункт назначения , называют планом (или матрицей) перевозок.

План перевозок , удовлетворяющий условиям (2.1) и (2.2), называется допустимым.

Допустимый план, в котором отличны от нуля не более 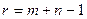перевозок равны нулю, называется опорным (или базисным).

Если в опорном плане перевозок число отличных от нуля перевозок в точности равно 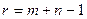, то план называется невырожденным, если меньше, то план называется вырожденным.

Тот план , который среди всех допустимых планов приводит к наименьшей стоимости всех перевозок, называется оптимальным.

2. Транспортная таблица

Условия транспортной задачи удобно оформить в виде так называемой транспортной таблицы (или матрицы планирования), поскольку методы решения этой задачи сводятся к операциям непосредственно с названными таблицами.

Грузы находящиеся в пунктах отправления, будем называть запасами, а грузы 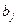, которые необходимо доставить в пункты назначения – заявками.

В транспортной таблице указываются

- пункты отправления (ПО) и пункты назначения (ПН),

- запасы пунктов отправления,

- заявки 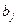пунктов назначения,

- стоимость перевозов из каждого i- го пункта отправления в каждый j- ый пункт назначения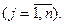

Стоимость перевозок записываются в правом верхнем углу каждой ячейки транспортной таблицы; в самой ячейке при составлении плана указывается перевозка

Составление транспортной таблицы и алгоритм решения транспортной задачи далее рассмотрим на конкретном примере.

Пример. На пунктах груз находится в количестве тонн соответственно. В пункты требуется доставить 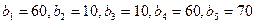тонн груза. Расстояния в сотнях километров между пунктами отправления и назначения приведены в матрице D:

Найти такой план перевозок, при котором общие затраты на перевозку грузов будут минимальными, считая стоимость перевозок пропорциональной количеству груза и расстоянию, на которое груз перевозится.

Для решения задачи использовать методы северо-западного угла и потенциалов.

Решение. Так по условию стоимость перевозок пропорциональна расстоянию, на которое груз перевозится, то матрицу D можно рассматривать как матрицу стоимости.

Составим транспортную таблицу задачи. Она имеет вид:

В первом столбце транспортной таблицы указываются запасы каждого из пунктов отправления. В нижней строке столбцы указываются заявки 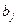каждого из пунктов назначения. Для транспортной задачи сумма запасов равна суме заявок; общее значение этой суммы записывается в правой нижней ячейке таблицы. В правом верхнем углу каждой ячейки транспортной таблицы записываются стоимости перевозки единицы груза из пункта отправления 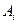в пункт назначения

Решение транспортной задачи сводится к следующему.

Нужно найти такие значения положительных перевозок, которые, будучи поставлены в базисных клетках транспортной таблицы, удовлетворяли бы следующим условиям:

- сумма перевозок в каждой строке таблицы должна быть равной запасу данного пункта отправления;

- сумма перевозок в каждом столбце должна быть равна заявке данного пункта назначения;

- общая стоимость перевозок должна быть минимальной.

Все действия по нахождению оптимального решения транспортной задачи сводится к соответствующим преобразованиям транспортной таблицы. При описании этих преобразований условимся через обозначать клетку стоящую в i -ой строке и j -м столбце транспортной таблицы.

3. Метод северо-западного угла нахождения опорного плана

Решение транспортной задачи, как и всякой задачи линейного программирования, начинается с нахождения опорного решения, или опорного плана перевозок. Для его составления можно использовать простейший метод – так называемый «метод северо-западного угла», состоящий в следующем.

Будем заполнять транспортную таблицу, начиная с её левого верхнего угла, условно называемого «северо-западным углом», т.е. с левой верхней ячейки (1, 1). Будем рассуждать при этом следующим образом.

1. В пункт требуется направить 70 тонн груза. Не учитывая стоимости перевозки единицы груза, удовлетворим заявку пункта за счет запасов пункта , отправив из этого пункта в пункт 60 тонн груза. В результате заявка пункта будет удовлетворена, а в пункте останется еще 10 тонн груза. Запишем указанную перевозку 60 тонн в клетке (1, 1).

2. Оставшиеся в пункте 10 тонн груза отправим в пункт ; эту перевозку запишем в клетке (1, 2). Запасы пункта исчерпаны, заявка пункта полностью удовлетворена.

3. Из запасов пункта направим 10 тонн груза в пункт 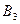; эту перевозку запишем в клетке (2, 3). Заявка пункта 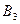полностью удовлетворена.

4. Оставшиеся в пункте 40 тонн груза отправим в пункт ; эту перевозку запишем в клетке (2, 4). Запасы пункта исчерпаны.

5. В составе заявки пункта остались неудовлетворенными еще 20 тонн груза. Это количество груза пошлем в из пункта ; перевозку, равную 20, запишем в клетке (3, 4). Заявка пункта полностью удовлетворена.

6. Оставшиеся в пункте 700 тонн груза направим в пункт ; эту перевозку запишем в клетке (3, 5).

На этом распределение грузов закончено: каждый пункт назначения получил руг согласно своей заявке. Это выражается в том, что сумма перевозок в каждой строке транспортной таблицы 2 равна соответствующему запасу, а в столбце-заявке.

Проанализируем составленный план, указанный в таблице 2. Очевидно, что этот план является допустимым, поскольку он удовлетворяет всем условиям (2. 1) и (2. 2). Допустимый план называют опорный, если в нем отличны от нуля не более 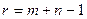базисных перевозок , а остальные перевозки равны нулю. В рассматриваемой задаче (число пунктов отправления грузов), 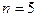(число пунктов назначения грузов) и таким образом . В составленном плане число отличных от нуля перевозок равно 6, т.е. меньше значения . Следовательно, составленный план перевозок является опорным. Однако особенностью этого плана является то, что в нем только 6 отличных от нуля перевозок, а для того, чтобы план был невырожденным, таких перевозок должно быть равно Поэтому план, представленный в таблице 2, является вырожденным, так как не хватает одной клетки, занятой перевозками. Нетрудно видеть, отчего это произошло: при распределении запаса груза 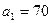, находившегося в пункте отправления , по пунктам и остаток оказался равным нулю и в соответствующую клетку не попал.

Дата добавления: 2014-12-24