Тема 4. Математическое программирование 4 страница

Благодаря выраженным оптимизационным свойствам выпуклых и вогнутых функций задача выпуклого программирования имеет достаточно эффективные методы решения.

Справедливы следующие теоремы.

Теорема 1. Пусть выпуклая (вогнутая) функция, замкнутое выпуклое множество, 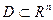. Тогда любой локальный минимум (максимум) на 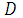является глобальным.

Теорема 2. Пусть выпуклая (вогнутая) функция достигает глобального минимума (максимума) в двух различных точках 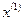и замкнутого выпуклого множества 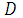. Тогда 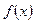достигает глобального минимума (максимума) и на бесконечном множестве точек, лежащих на отрезке, соединяющем точки и .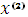

Теорема 3. Пусть строго выпуклая (вогнутая) функция, замкнутое выпуклое множество. Тогда существует единственная точка, в которой достигает глобального минимума (максимума).

Теорема 4. Пусть выпуклая (вогнутая) функция является непрерывной вместе со своими частными производными первого порядка во всех внутренних точках замкнутого выпуклого множества . Пусть градиент функции равен нулю в некоторой точке , т.е. . Тогда функция в точке достигает глобального минимума (максимума).

Теорема 5. Множество решений системы неравенств

выпукло, если выпуклые функции рассматриваются со знаком , а вогнутые со знаком .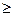

Доказательства теорем можно найти в .

В задачах выпуклого программирования широко распространен метод решения, основанный на применении теоремы Куна Таккера: Теорема обобщает метод множителей Лагранжа для классической задачи оптимизации, с ограничениями в виде равенств, на задачи нелинейного программирования с ограничениями в виде нестрогих неравенств.

Классическая задача оптимизации формулируется и решается следующим способом.

Дано:

1) непрерывная и дифференцируемая функция нескольких переменных ,

2) на переменные наложены условия – ограничения в виде равенств

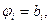
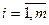(3.15)

где функции непрерывны и дифференцируемы.

Найти такие точки 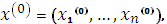в которых функция

(3.16)

достигает максимума (минимума).

Задачи (3.5), (3.6), (3.7), (3.8), (3.15), (3.16) называются задачами на условный экстремум. Задача (3.15), (3.16) отличается тем, что условия ограничения представлены в виде равенств и .

Задача (3.15), (3.16) решается методом множителей Лагранжа с помощью составления функции Лагранжа: линейной комбинации целевой функции и функций ограничений, наложенных на переменные

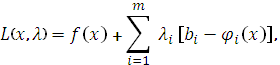
(3.17)

где дополнительно вводимые неотрицательные переменные, называемые множителями Лагранжа, , , .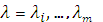

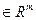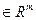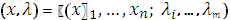Чтобы решить задачу необходимо найти частные производные функции Лагранжа по и 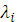, приравнять их нулю и решить полученную систему 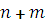уравнений (необходимые условия):

(3.18)

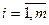, , (3.19)

решением будет некоторое множество стационарных точек 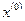функции Лагранжа.

В каждой точке 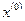целевая функция имеет локальный условный экстремум, ранг матрицы 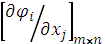равен .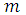

Из стационарных точек, взятых без координат , выбрать точки, в которых функция имеет локальные условные экстремумы при выполнении ограничений равенств .

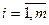Этот выбор выполняется с применением, например, достаточных условий локального экстремума.

В основе метода Лагранжа используется идея о возможности заменить целевую функцию, в ее области допустимых решений, функцией Лагранжа, безусловный экстремум которой совпадает с условным экстремумом целевой функции .

Подчеркнем, что метод множителей Лагранжа устанавливает всего лишь необходимые условия, которым должна удовлетворять точка 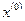, доставляющая целевой функции локальный условный экстремум. В задачах же выпуклого программирования найденная точка 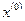будет одновременно и точкой глобального экстремума.

Теорема Куна – Таккера. Пусть: 1) для задачи (3.5), (3.6) составлена функция Лагранжа

() = + (3.20)

где – непрерывные и дифференцируемые функции,

2) существует, по крайней мере один, вектор , для которого справедливы строгие ограничения

0, 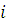= (условие регулярности Слейтера), (3.21)

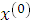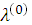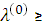3) существует вектор (, ) = (,…, , ,…, ) такой, что при 0, 0 справедливо

L(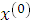, λ) ≤ L(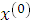, 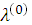) ≤ L(x, 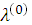), (3.22)

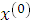() = 0. (3.23)

Тогда целевая функция (3.5) достигает минимума в точке 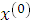= (,…, ) [3].

Иногда теорема Куна – Таккера называется теоремой о седловой точке, поскольку точка (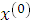, 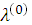) = (,…, , ,…, ) является седловой точкой функции Лагранжа (3.20).

Условия (3.22) эквивалентны локальным условиям Куна – Таккера:

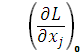
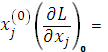
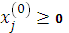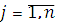, , , , (3.24)

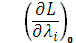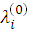
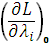≤ 0, = 0, 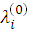, 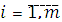. (3.25)

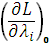
Здесь , значение частных производных функции Лагранжа в седловой точке (, ).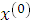

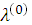Локальные условия (3.24), (3.25) являются необходимыми и достаточными уловиями существования седловой точки (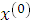, 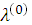) функции Лагранжа (3.20).

Для задачи (3.7), (3.8) теорема Куна – Таккера формулируется аналогично. При поиске максимума вогнутой функции выражения (3.20), (3.22), (3.23), (3.24), (3.25) принимают вид:

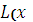, λ) = + , (

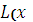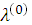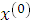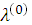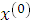, ) ≤ (, ) ≤ (, λ), (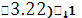

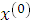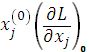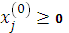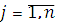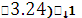
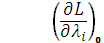() = 0, (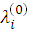

, , , , (

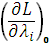≤ 0, = 0, , . (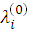

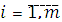Из 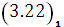следует, что в седловой точке максимальное значение функции Лагранжа достигается по переменным и минимальное по переменным .

Заметим также, что возможен переход от задачи (3.7), (3.8) к задаче (3.5), (3.6). Для этого необходимо выражения (3.7), (3.8) умножить на 1 и применить соответствующие задаче (3.5), (3.6) условия теоремы КунаТаккера. Аналогично осуществляется переход от задачи (3.5), (3.6) к задаче (3.7), (3.8) [4].

Дата добавления: 2014-12-24