Провести построение разностной схемы Рунге-Кутта с погрешностью аппроксимации 2-го порядка точности

Определить локальную и глобальную погрешность решения задачи Коши разностным методом. Провести построение метода Рунге получения апостериорной погрешности решения. Как используется метод Рунге для автоматического выбора шага сетки аргумента.

Дать определение погрешности решения, погрешности аппроксимации, аппроксимации и сходимости разностной схемы. Провести исследование аппроксимации и сходимости явной и неявной разностной схемы метода Эйлера.

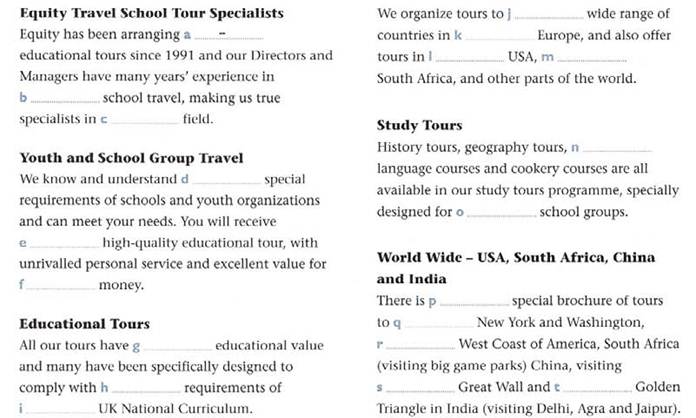
Exercise 11. Complete the text with a/an, the or leave blank for zero article.

Exercise 10. Complete the text with a/an, the or leave blank for zero article.

Exercise 9. Complete the text with a/an, the or leave blank for zero article.

Пример. Аппроксимирует ли разностная схема

Задачу Коши (ЗК) 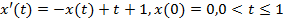. С каким порядком?

Общий случай: - разностная схема, L(u)=0 – непр. задача, y – точное решение разностной схемы, u – точное решение ЗК.

Величина наз погрешностью аппроксимации разностной схемы исх задачи. (Смысл опр: хотим определить, насколько дискретная модель отличается от исходной)

Погр аппрокс разностной исх зад на точном решении равна невязке.

Математическое понятие аппроксимации: Разностная схема аппроксимирует исходную задачу, если , аппроксимация порядка P, если 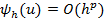(т.е при бесконечном дроблении сетки арг )

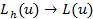Для метода Эйлера p=1

Уст разностной схемы

Запишем

Разностная схема устойчива, если 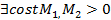, не зависящие от h и выбора u_0 и f, что им место нер-во 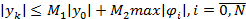а) если 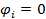, а , то имеет место ; б) , то имеет место уст по правой части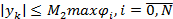

Если шаг 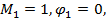то 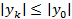– уст по начальным данным.

Если шаг 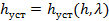(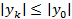), то условная устойчивость.

Всё сказанное справедливо и для систем ДУ, только вместо абс вел-ны ставим норму.

Сходимость разностных схем и погрешность.

Теорема: Пусть исх зад z(u)=0 пост корр-но и разн схема аппроксимирует разн схему с пар-ом 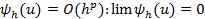, h → 0. И пусть разн сх уст, тогда разн сх сх-ся, т.е 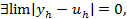h → 0. Причем сх-ся с порядком = погрешности аппрокс-ии

Док-во: 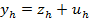подставим в разн сх метода Эйлера:

Из усл. устойч.: и на основании леммы (из уст. по нач. данным след. уст. по пр. части) и 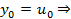(*) . С другой стороны р.сх. также аппрокс. решение, т.е. с порядком р 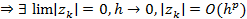. (В случае разн. сх. Эйлера р=1).

Замечание: 1. Из сходимости разн сх => что мы можем получить решение с любой наперед заданной точностью. Она будет достигнута соответствующим дроблением сетки аргумента; 2. Из полученной оценки погрешности (*) =>что порядок погрешности носит суммарный или глобальный характер. Поэтому 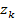будем рассматривать как глобальную погрешность.

Разн сх является корректно заданной, если она аппрокс уст и сх-ся. Разн сх Эйлера условно уст (шаг выбирают из условия – оценка правой части). Нужно выбирать маленький шаг, чтобы если функция решения сильно изменится, не изменилась правая часть на большую величину.

Пример: да аппроксимирует с порядком p=1. (т.к. это р.сх. Эйлера, а для нее доказано, что погрешность аппроксимации ).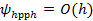

Сходимость разностных схем и погрешность.

Теорема: Пусть исх зад L(u)=0 пост корр-но и разн схема аппроксимирует разн схему с пар-ом 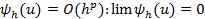, h → 0. И пусть разн сх уст, тогда разн сх сх-ся, т.е 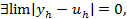h → 0. Причем сх-ся с порядком = погрешности аппрокс-ии

Док-во: 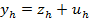подставим в разн сх метода Эйлера:

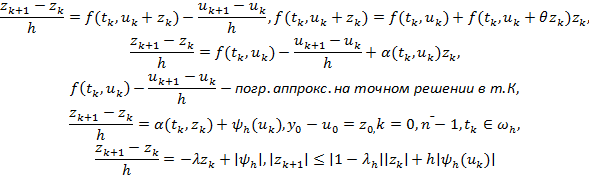
Нашли, что усл устойчиво: и на основании леммы, что правая часть уст (*)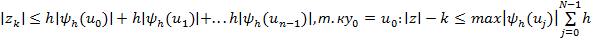

из условия теоремы об устойчивости: т.к аппрокспорядка р, то , в случае разн сх Эйлера р=1.

Замечание: 1. Из сходимости разн сх => что мы можем получить решение с любой наперед заданной точностью. Она будет достигнута соответствующим дроблением сетки аргумента; 2. Из полученной оценки погрешности (*) =>что порядок погрешности носит суммарный или глобальный характер. Поэтому 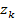будем рассматривать как глобальную погрешность.

Разн сх является корректно заданной, если она аппрокс уст и сх-ся. Разн сх Эйлера условно уст (шаг выбирают из условия – оценка правой части). Нужно выбирать маленький шаг, чтобы если функция решения сильно изменится, не изменилась правая часть на большую величину.

Построение разностной схемы с переменным шагом h.

Введём понятие локальной погрешности.

Опр. Погрешность локальная (на шаге) определяется так: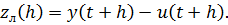

- получение конечного решения разностной схемы с точным начальным условием.

Для м. Эйлера: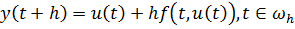

Проведём исследование локальной погрешности в виде порядка малости шага h.

Пусть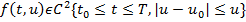

Представим локальную погрешность используя формулу Тейлора (на шаге):

Обобщим для метода порядка

Опр. 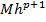называется главным членом локальной погрешности. называется избыточной гладкостью решения (т.к для оценки погрешности нужно брать степеней 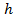, а тут ).

Правило или метод Рунге.

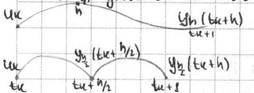На отрезке длиной h с н.у.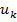

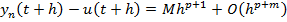
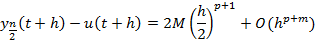
Чтобы исп. формулы для получения практического решения нужно из оценки исключить неизвестную величину .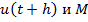

Из 2 вычитаем 1:

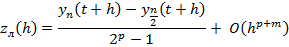
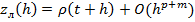- мы м. получить её реально при вычислениях и оценить локальную погрешность.

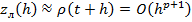
На основании этого строится схема вычисления локальной погрешности на каждом шаге, если задана точность и после вычисления величин окажется, что 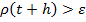, тогда применим автоматический выбор шага.

Автоматический выбор шага.

Используется для получения заданной точности решения в каждой точке аргумента.

Это адаптивная (самонастраиваемая) процедура.

Если

При каких-то .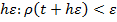

Получим 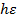и решение дальше, но функция меняется и шаг может быть не экономичен, тогда мы удваиваем шаг. И если получаем, что

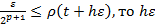не изменяем.

Пример. Привести алгоритм автоматического выбора шага аргумента при решении методом Эйлера задачи Коши

Запишем разностную схему:

. Пусть

Тогда согласно методу Рунге считаем на каждой итерации один раз с шагом h и два раза с шагом h/2. Затем берем разность полученных значений как оценку погрешности (надо делить на – для метода Эйлера p=1, т.е. делить не нужно). Примерный алгоритм автоматического выбора шага:

1) ;

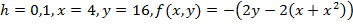2) .

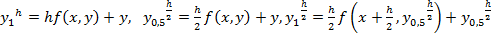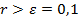. Если то 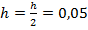и повторяем шаг. Если , то 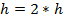и переходим к следующей итерации. В противном случае переходим на следующую итерацию, не меняя шаг.

.

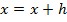3) . .

.......................................................

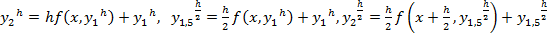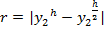И продолжаем цикл до тех пор, пока не найдем значения в точке 7 (пока ).

Пример. Построить такую разностную схему с точностью аппроксимации 10^-3 для задачи

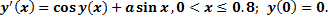
Ответ:

Рассмотрим задачу Коши для ДУ: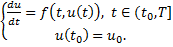

Интегрируем уравнение на очень малом шаге :

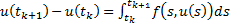
По формуле левых прямоугольников: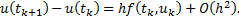

Если 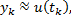то получим:

Можно использовать: .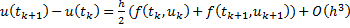

Тогда замена будет

В этом случае надо решать нелинейное уравнение для нахождения . Это нелинейное уравнение – решать методом Ньютона (например) 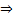эта формула неэкономична.

Тогда будем решать: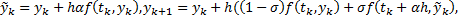

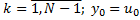– формула одношаговая, т.к. для нахождения последующего значения нужно знать одно предыдущее; формула явная (т.к. нет нелинейных уравнений) и здесь 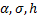- выбираются таким образом, чтобы совокупность этих формул давала погрешность аппроксимации 2-го порядка малости по h и чтобы разн. схема сходилась по h и была устойчивой.

Найдем . Заметим, что .

Разностную схему представим в следующем виде:

Вспомним, что погрешность аппроксимации = невязке разностной схемы на точном решении:

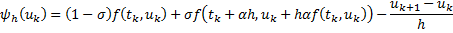
Стандартный прием – разложение в ряд всех точных решений, встреч. в этой записи.

Пусть . Тогда :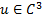

а) 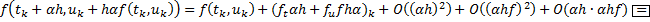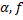-ограниченные величины, поэтому порядок малости .

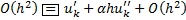б) представим по формуле Тейлора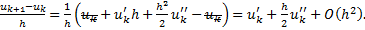

Подставим а), б) в выражение погрешности аппроксимации:

1) 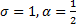, тогда погрешность аппроксимации будет второго порядка малости

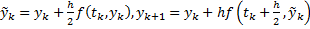– формула Рунге-Кутта 2-го порядка. Она 2-х этапная, одношаговая, явная:

Данная формула также называется «предиктор-корректор».

2)

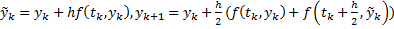–формула Рунге-Кутта, одношаговая, явная 2-х этапная.

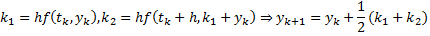
Итак, теперь 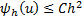, а из того, что 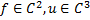следует, что 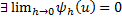и разностная схема аппроксимирует исходную задачу с порядком h.

Пример. Построим такую разностную схему с точностью аппроксимации 10^-3 для задачи

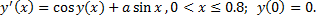
Так как , то .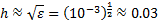

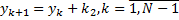
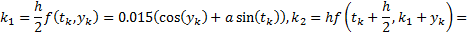
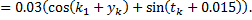
В нашем случае .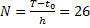

Дата добавления: 2014-12-23