Лекция 6. Обратная матрица и методы ее вычисления. Матричные уравнения

Определение. Квадратная матрица называется вырожденной (или особенной), если её определитель равен нулю, и невырожденной (или неособенной) - в противоположном случае.

Определение. Матрица 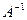называется обратной по отношению к квадратной матрице 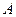, если .

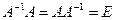Теорема. Квадратная матрица 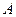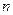-го порядка имеет обратную матрицу 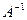, причем единственную, тогда и только тогда, когда матрица 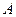невырожденная. В этом случае обратная матрица вычисляется по следующей формуле:

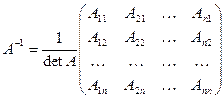, где 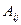- алгебраическое дополнение элемента 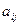матрицы .

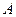Рассмотрим пример: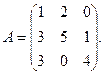

det A = 20 + 6 – 24 = 2;

.

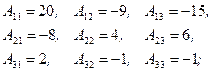
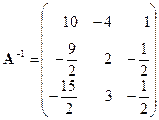Еще раз подчеркнем, что обратная матрица существует только для квадратной матрицы с определителем, отличным от нуля.

Для невырожденных матриц выполняются следующие свойства:

1.

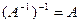
2.

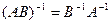
3.

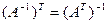
4.

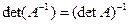
Теорема. Определитель произведения нескольких матриц 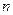- го порядка равен произведению определителей этих матриц.

Пусть имеется матрица A = (a_ij) размерности m ´ n, n -мерный вектор-столбец X и m- мерный вектор-столбец B:

; .

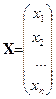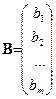Тогда матричное равенство

AX = B, (1)

если расписать его поэлементно, примет вид:

.

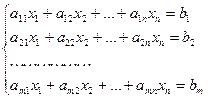Таким образом, формула (1) является записью системы m линейных уравнений с n неизвестными в матричной форме. Такая запись, кроме краткости написания, позволяет получить еще один метод решения систем линейных алгебраических уравнений..

Пусть мы имеем квадратную систему линейных уравнений:

.

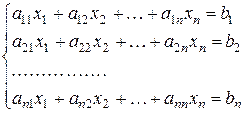Ее можно записать в матричной форме:

AX = B,

где

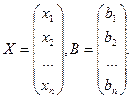
Если определитель матрицы A не равен нулю, то система имеет единственное решение, определяемое формулой:

.

Если даны квадратные матрицы 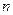-го порядка 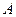и , из которых 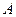— невырожденная, а произвольная, то мы можем выполнить правое и левое деления на 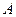, т.е. решить матричные уравнения .

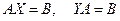Для этого, ввиду ассоциативности умножения матриц, достаточно положить, 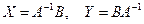, причем 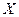и 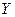будут, ввиду некоммутативности умножения матриц, в общем случае различными.

Дата добавления: 2014-12-24