Лекция 11. Прямая линия на плоскости. Различные виды уравнений на плоскости. Расстояние от точки до плоскости. Взаимное расположение двух прямых

Теорема. На плоскости в прямоугольной системе координат всякое уравнение первой степени 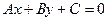задает прямую линию.

Уравнение вида 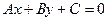, где 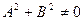, называется общим уравнением прямой 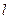. Вектор 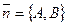ортогонален прямой 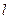и называется нормальным вектором этой прямой.

Любой ненулевой вектор, параллельный данной прямой, называется ее направляющим вектором. В случае, когда прямая задана общим уравнением, то направляющий вектор будет иметь вид .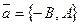

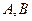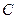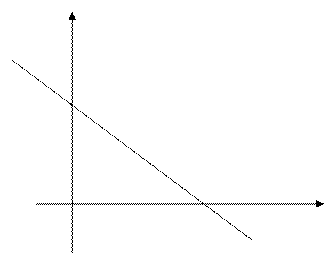
Если в общем уравнении прямой все его коэффициенты и отличны от нуля, то его можно привести к виду 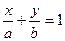, которое называется уравнением прямой в отрезках.

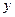
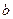
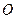
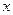
Пусть на плоскости выбрана система координат, и в этой системе известны координаты некоторой точки 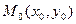прямой 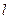и направляющего вектора 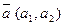этой прямой.

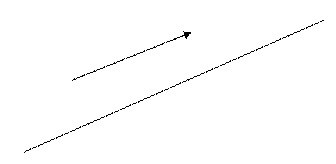
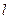
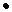
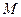
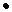
Очевидно, что точка 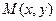принадлежит прямой 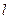тогда и только тогда, когда векторы и 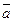коллинеарны. Используя условие коллинеарности векторов, получим

.

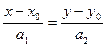Это уравнение обычно называют каноническим уравнением прямой.

Заметим, что в каноническом уравнении один из знаменателей может оказаться равным нулю (оба знаменателя не могут равняться нулю, ибо вектор 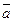ненулевой). В этом случае обращение в нуль одного из знаменателей будет означает обращение в нуль и соответствующего числителя.

Если заданы две точки 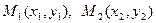прямой 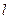, то уравнение этой прямой будет иметь вид

.

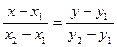Если за параметр 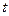принять величину, стоящую в левой и в правой частях канонического уравнения, то получим параметрические уравнения прямой

.

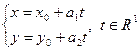Пусть дана прямая, пересекающая ось ординат. Если 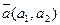- направляющий вектор прямой, то и 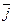не коллинеарны, поэтому 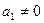. Число 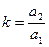называется угловым коэффициентом прямой. Тогда из канонического уравнения прямой получим 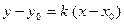. Если в качестве 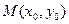взять точку 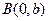пересечения прямой с осью ординат, то придем к уравнению

.

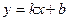Это уравнение называется уравнением прямой с угловым коэффициентом.

Введем понятие угла между двумя прямыми. Пусть две прямые 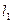и 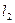заданы общими уравнениями: .

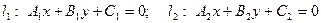Углом между этими прямыми будем называть угол между векторами нормали этих прямых.

Тогда угол 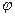между этими прямыми будет вычисляться по формуле

.

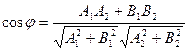Условие параллельности прямых 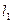и 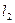эквивалентно условию коллинеарности векторов нормали этих прямых. То есть

.

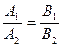Условие совпадения прямых 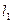и 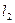имеет вид: .

Условие перпендикулярности прямых 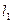и 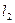выражается равенством нулю скалярного произведения векторов нормали, то есть 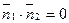. Отсюда получаем условие

.

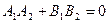Теперь определим нормированное уравнение прямой.

Рассмотрим произвольную прямую 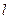. Проведем через начало координат 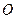прямую 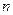, перпендикулярную 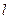, и обозначим буквой точку пересечения указанных прямых.

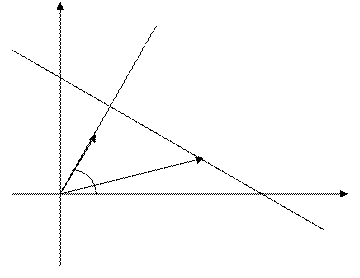
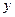
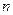
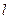
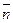
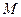
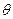
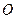
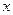
На прямой 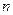возьмем единичный вектор 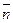, направление которого совпадает с направлением отрезка 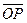(в случае совпадения точек 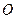и направление 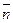выберем произвольно). Выразим уравнение прямой 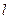через длину отрезка 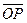и угол 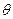между вектором 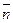и осью .

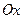Так как 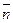- единичны вектор, то его координаты имеют вид .

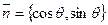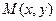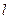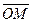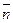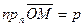Точка лежит на рассматриваемой прямой тогда и только тогда, когда проекция вектора на ось, определяемую вектором , равна , то есть при условии . Но с другой стороны, 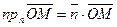. Отсюда получаем уравнение

.

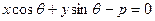Это уравнение и называется нормированным уравнением прямой.

Для приведения общего уравнения прямой 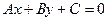к нормированному виду следует умножить его на нормирующий множитель 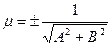, знак которого выбирается противоположным знаку .

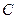Теорема. Пусть прямая 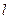задана уравнением 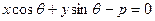. Тогда расстояние от точки 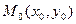до данной прямой вычисляется по формуле

.

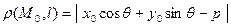Следствие 1. Расстояниеот точки 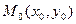до прямой 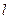, заданной уравнением 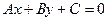вычисляется по формуле

.

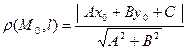Дата добавления: 2014-12-24