Примеры непосредственного вычисления вероятностей

Относительная часть случайного события. Статистическое и классическое определения вероятности случайного события.

Определение:

Относительной частотой Р* случайного события А, называется отношение числа m* случаев появления данного события к общему числу n* проведенных одинаковых испытаний, в каждом из которых могло появиться или не появиться событие А.

Будем обозначать:

.

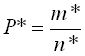Пример 1.2.1.

Пусть по данному объекту из 6 одинаковых орудий произведен залп. Число попаданий равно 2. Событие А — попадание в цель. Относительная частота попаданий Р будет равно

.

Пример 1.2.2.

Отдел технического контроля обнаружил 3 нестандартных детали в партии из 100 случайно отобранных деталей.

Относительная частота появления нестандартных деталей

.

Опыт показывает, что существует постоянное число Р такое, что при достаточно большом числе испытаний относительная частота Р* появления события А мало отличается от этого числа:

, .

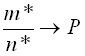Число Р называется вероятностью появления случайного события А. Это так называемое статистическое определение вероятности. В этом случае говорят, что относительная частота Р* сходится по вероятности к вероятности Р;это означает, что для произвольного ε >0, начиная с некоторого номера испытаний N, найдется n* такое, что хотя n*>N, неравенство |Р*-Р|<ε выполняется не для всех n*, а для подавляющего числа испытаний n*, т.е. сходимость по вероятности Р*→Р нельзя понимать как предельный переход т.к. последнее условие требует выполнения неравенства |Р*-Р|<ε для всех n*>N при соответствующем с> 0.

Перейдем к классическому определению вероятности. Назовем каждый из возможных результатов испытаний, т.е. каждое событие, которое может наступить в испытании элементарным исходом. Те элементарные исходы, при которых интересующее нас событие наступает, назовем благоприятствующими этому событию.

Пример 1.2.3.

При однократном бросании игральной кости возможные исходы — выпадание одного из чисел 1,2,3,4,5,6,. Таким образом, имеется шесть элементарных исходов.

Пример 1.2.4.

При одновременном бросании двух игральных костей возможные исходы — выпадание одного из чисел i на грани первой игральной кости сочетается с 6 числами j (1,2,3,4,5,6), выпадающими на гранях второй игральной кости, т.к. i принимает 6 значений (1,2,3,4,5,6), то общее число сочетаний ij состоит из 36 исходов.

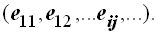
Пример 1.2.5.

В урне n строго разноцветных шаров. Извлекаются подряд два шара. Возможные исходы - извлечение двух разноцветных шаров. Каждое из n первых извлечений сочетается c (n -1) вторым извлечением. Общее число сочетаний n (n -1).

Определение:

Вероятностью случайного события А называется отношение числа m благоприятствующих этому событию случаев к числу всех возможных случаев n, образующих полную группу равновозможных событий. Символически вероятность записывается в виде Р (А).

.

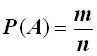Из определения вероятности вытекает следующее:

1. Вероятность достоверного события А равна единице, поскольку все элементарные исходы благоприятствуют этому событию;

.

2. Вероятность невозможного события А равна нулю, поскольку ни один элементарный исход не благоприятствует этому событию;

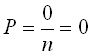
Вероятность любого события А удовлетворяет неравенству:

0 ≤ Р(А) ≤ 1.

Напомним элементарные сведения из теории соединений. Рассмотрим соединения, состоящие из n элементов а₁,а₂,…,а_n.

Различают три вида соединений: перестановки, размещения и сочетания.

Перестановками Р_п из n элементов называются такие соединения, содержащие по n элементов и отличающиеся друг от друга порядком элементов а₁,а₂,…,а_n.

Подсчитаем количество перестановок из п элементов а₁,а₂,…,а_n.

Первый элемент в перестановке можно выбрать п способами (по числу элементов), второй элемент (п -1) способом, третий (п - 2) способами и т.д. Число способов, которыми можно выбрать два первых элемента, равно п (п -1), три первых элемента n (n -l) (n -2) и т.д.

Следовательно, число перестановок на п -элементов равно P_n = n (n -l)(n -2)....l= n!,

где п! произведение натуральных чисел от 1 до п.

Пример 1.3.1.

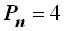!= 4·32·1=24.

Размещениями из п элементов по m элементов (обозначается 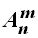)называются такие соединения, в каждое из которых входит m элементов, взятых из данных п элементов и которые отличаются друг от друга либо самими элементами, либо порядком их расположения. Подсчитываем количество размещений 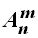из п элементов;

.

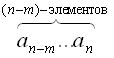Первый элемент в размещениях можно выбрать п -способами, последний (n-m +1) способами.

Следовательно, число размещений из n -элементов по m найдем из выражения:

.

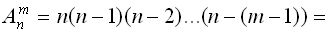
Пример 1.3.2.

.

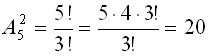Сочетаниями из п -элементов no m называет соединения, в каждое из которых входит m элементов, взятых из п -элементов и которые отличаются друг от друга элементами (по крайней мере, одним элементом).

Очевидно, , .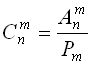

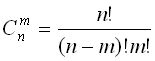Пример 1.3.3.

.

Пример 1.3.4.

В партии из 10 деталей имеются 7 стандартных деталей. Найти вероятность того, что среди шести взятых наудачу деталей будет 4 стандартных.

Решение: Общее число возможных исходов испытаний равно числу способов, которыми можно извлечь 6 деталей из 10, т.е. числу сочетаний из 10 элементов по 6 .

Подсчитаем число исходов, благоприятствующих интересующему нас событию — среди шести взятых деталей 4 стандартных; 4 стандартные детали можно взять из 7 стандартных деталей способами, при этом остальные 6-4=2 детали должны быть нестандартными; взять же 2 нестандартные детали из 10-7=3 нестандартных деталей можно 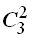способами. Следовательно, число благоприятствующих исходов равно:

· .

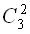Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

.

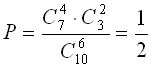Пример 1.3.5.

По цели осуществляется залп из двух орудий. Вероятность попадания в цель из первого орудия 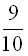, из второго 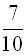. Какова вероятность поражения цели,если для этого достаточно хотя бы одного попадания.

Решение:

Промоделируем задачу схемой с урнами. В первой урне 10 шаров - из них 9 красных. Во второй урне 10 шаров - из них 7 красных. По условию задачи необходимо подсчитать вероятность извлечения двух шаров (по шару из каждой урны), хотя бы один из которых был бы красный. Найдем общее количество исходов. Одно извлечение из первой урны сочетается с 10 извлечениями из второй урны; т.к. всего таких извлечений из первой урны в 10 раз больше, то общее количество исходов - 100. Подсчитаем общее количество благоприятствующих исходов: 9 красных шаров из первой урны будут сочетаться с 10 шарами второй урны, что дает 90 исходов, и один не красный шар из первой урны будет сочетаться с семью красными шарами из второй урны, давая 7 исходов. Следовательно, общее количество исходов, в которых будет присутствовать хотя бы один красный шар — 97.

Искомая вероятность равна:

.

Пример 1.3.6.

Найдем в условиях предыдущей задачи вероятность только одного попадания в цель. Решение задачи опять промоделируем схемой урн.

В первой урне 10 шаров, из них 9 красных, во второй — 7 красных. По условию задачи необходимо найти вероятность извлечения двух шаров (по одному из каждой урны), чтобы только один из них был красный. Общее число исходов, как и в предыдущей задаче, — 100.

Число благоприятствующих исходов равно сумме числа сочетаний при извлечении 9 красных шаров из первой урны с 3 не красными шарами второй урны и 7 красных шаров второй урны с 1 не красным шаром первой урны, т.е. 9 3+1·7=34. Искомая вероятность .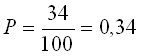

Последнее условие можно записать в виде:

.

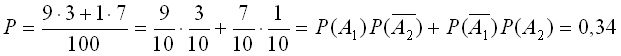где А₁, А₂ — события, сводящиеся к извлечению красных шаров из первой и второй урн, соответственно события, сводящиеся к извлечению не красного шара из первой и второй урн, соответственно.

Пример 1.3.7.

Найдем в условиях предыдущей задачи вероятность одновременного попадания в цель. Решение задачи промоделируем схемой урн. По условию задачи необходимо найти вероятность извлечения двух красных шаров. Общее число исходов — 100. Число благоприятствующих исходов 9·7=63.

Искомая вероятность .

Пример 1.3.8.

Ткацкий станок (швейная машина) работает в течение 8 часов с остановками, вызванными обрывом нити. Общая продолжительность простоя станка составляет 1/6 часа. Найти вероятность обрывной работы станка.

Решение:

Предположим, что на протяжении 8 часов событие „обрыв нити" и событие „безобрывная работа" ткацкого станка равновозможны в любой момент времени. Тогда общее количество исходов пропорционально общему времени наблюдения за работой станка.

Количество исходов, приводящее к обрыву нити, пропорционально интервалу времени простоя станка из-за обрывов, т.е. 1/6 часа. Искомая вероятность обрывной работы станка

.

Работу, например 2-х станков, если заданы вероятности их работы 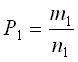и также можно промоделировать схемой урн.

Пример 1.3.9.

N человек извлекает из урны, наполненной, п билетами, один выигрышный билет. Найти вероятность извлечения выигрышного билета. Общее число исходов равно числу всевозможных последовательных очередностей извлечений билетов. Первый человек может извлечь билет п способами, второй(п -1) способами и т.д. Общее число последовательностей п!. Число благоприятствующих последовательностей когда уже нужный билет выбран, равно (п -1)!

Искомая вероятность .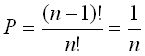

Пример 1.3.10.

В первой урне п₁ шаров, из них m₁ красных. Во второй урне п₂ шаров, из них m₂ красных. Из второй урны в первую наугад переложен шар. Найти вероятность Р (А) извлечения из первой урны красного шара (событие А).

Для решения задачи воспользуемся классическим определением понятия вероятности случайного события

.

Подсчитаем полную группу событий: число п извлечений шара из первой урны, после того как туда переложен шар из второй урны. При каждом из п₂ переложенном шаре из второй урны возможно (n₁ +1) извлечений шара из первой урны.

Следовательно, n = n₂ (n₁ + l), подсчитаем число m благоприятствующих исходов извлечения красного шара из первой урны, очевидно,

.

Искомая вероятность равна

,

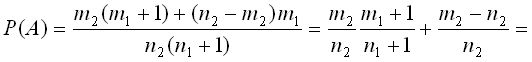
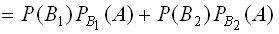где P (B₁), P (B₂) — вероятности извлечения соответственно красного из второй урны и белого шаров 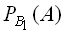и — условные вероятности извлечения из первой урны красного шара, вычисленные при условии, что в первую урну был переложен, соответственно, красный и белый шары.

Дата добавления: 2014-12-25