Теоретическая часть. Цель работы: изучение колебаний математического и физического маятников; определение ускорения свободного падения

МАТЕМАТИЧЕСКИЙ И ФИЗИЧЕСКИЙ МАЯТНИКИ

Лабораторная работа № 8

Цель работы: изучение колебаний математического и физического маятников; определение ускорения свободного падения.

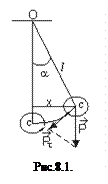
Простейшим примером гармонических колебаний является движение так называемого математического маятника. Математическим маятником называется маятник, состоящий из материальной точки массой m, подвешенной на невесомой нерастяжимой нити длиной 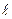и колеблющейся около точки подвеса О. В этом случае центр тяжести системы можно считать совпадающим с центром тяжести груза. Напишем уравнение движения для математического маятника, находящегося в поле тяготения и отклоненного от состояния равновесия на угол a. Система, выведенная из состояния устойчивого равновесия и предоставленная самой себе, совершает колебания, называемые свободными. На маятник в отклоненном состоянии действует составляющая силы тяжести (рис. 8.1) 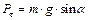. Она направлена по касательной к траектории груза в сторону положения равновесия. Уравнение движения груза будет иметь вид:

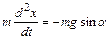. (8.1)

В этой записи уравнения учтено, что возвращающая сила всегда направлена в сторону, противоположную направлению возрастания смещения х. При малых отклонениях маятника от положения равновесия (угол a не превышает 5–6 град.) можно считать, что 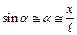, т.е. смещение по дуге можно считать приближенно равным смещению вдоль горизонтальной хорды. Уравнение (8.1) обычно записывается в виде:

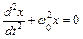, (8.2)

где 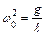– циклическая частота гармонических колебаний.

Решением этого дифференциального уравнения является выражение: 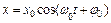. Период колебаний маятника определяется формулой:

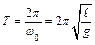. (8.3)

Из этой формулы видно, что период колебаний математического маятника зависит только от ускорения силы тяжести в данном месте Земли и от длины маятника, и не зависит от амплитуды колебаний и от массы груза. Измеряя Т и используя формулу (8.3), можно вычислить ускорение свободного падения в данном месте земной поверхности.

Рис.8.2.

Этим методом впервые было измерено значение g на разных широтах земного шара, в результате чего была установлена зависимость g от широты j. Если измерить для нескольких значений 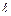соответствующие периоды колебаний (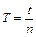, где t − время n полных колебаний), затем построить график зависимости Т² от 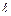, то согласно формуле (8.3) эта зависимость может быть представлена в виде прямой типа: 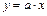. Тангенс угла наклона этой прямой численно равен: 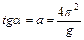. Отсюда можно найти ускорение свободного падения: .

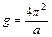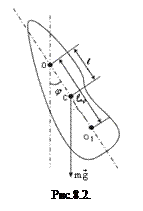Другой колебательной системой, с помощью которой можно определить ускорение свободного падения, является физический маятник. Физическим маятником называется твердое тело, совершающее под действием силы тяжести колебания относительно неподвижной оси, проходящей через точку О, не совпадающую с центром масс С тела (рис. 8.2).

Из-за наличия трения часть механической энергии маятника рассеивается в виде тепла, поэтому колебания всегда затухают. Так как маятник совершает вращательные колебания, то они описываются основным уравнением динамики вращательного движения отно- сительно неподвижной оси:

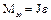, (8.4)

где – момент инерции маятника относительно оси, проходящей через точку О; J₀ – его момент относительно центра масс; 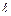- расстояние от точки О до центра масс С; m – масса маятника; 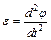– угловое ускорение; М_w – проекция на ось вращения результирующего момента всех сил, действующих на тело. Результирующий момент сил складывается из вращательного момента, создаваемого силой тяжести 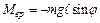, и тормозящего момента, создаваемого силами трения 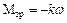, где k – коэффициент затухания, 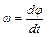– угловая скорость. Знак «–» в формуле для вращательного момента отражает тот факт, что возвращающая сила всегда направлена к положению равновесия, а в формуле для тормозящего момента то, что сила трения направлена против направления движения.

При малых углах отклонения 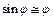, тогда 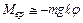, и уравнение (8.4) можно представить в виде:

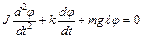. (8.5)

Введя обозначения: 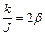, где b – коэффициент затухания; 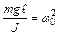, w₀ – собственная частота маятника, получаем универсальный вид дифференциального уравнения свободных затухающих колебаний:

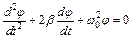, (8.6)

его решением является функция:

, (8.7)

где 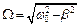– частота свободных затухающих колебаний, 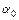– начальная фаза.

Период свободных затухающих колебаний можно найти по формуле:

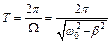. (8.8)

Если считать, что затухание колебаний мало (см. конструкцию прибора), то им можно пренебречь в выражении (8.8). Учитывая, что 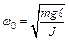получаем для периода колебаний физического маятника следующую формулу:

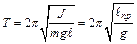. (8.9)

где 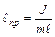– приведенная длина физического маятника. Приведенная длина физического маятника – это длина такого математического маятника, период колебаний совпадает с периодом данного физического маятника.

Точка на прямой, соединяющей точку подвеса с центром масс, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (см.точку О' на рис 8.2). При подвешивании маятника в центре качания О' приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания. На этом свойстве основано определение ускорения свободного падения с помощью так называемого оборотного маятника. Оборотным маятником называется такой маятник, у которого имеются две параллельные друг другу, закрепленные вблизи его концов опорные призмы, за которые он может поочередно подвешиваться. Вдоль маятника могут перемещаться и закрепляться на нем тяжелые грузы. Перемещением грузов добиваются того, чтобы при подвешивании маятника за любую из призм период колебаний был одинаков. Тогда расстояние между опорными ребрами призм будет равно 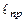. Тогда значение ускорения свободного падения 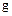можно найти по формуле:

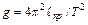. (8.10)

Дата добавления: 2014-12-25