Робота сили ваги 2 страница

2 См. подробнее: Samuels S.M., Wilkes F.M., Pragshaw R.E. Management of Company Finance. – L.: Chapman & Hall, 1993. – Р.635.

3 Chapman C. Now the Stock Markets Work. – Z.: Century. Business Book, 1994. – Р.134.

1 См. подробнее: Samuels S.M., Wilkes F.M., Pragshaw R.E. Management of Company Finance. – L.: Chapman & Hall, 1993. – Р.697.

1 The British Telecom company annual Report. – 1996, 1997.

[226] Bodie Z., Kane A., Markus A., Perrakis S., Pyan P. Investments. — P. 415.

[227] Ibid. — P. 416.

[228] Шарп У. Ф., Александер Г. Дж., Бэйли Дж. В. Инвестиции. — 1997. — С. 108.

[229] Шарп У. Ф., Александер Г. Дж., Бэйли Дж. В. Инвестиции. — 1997. — С.109.

[230] Див. докладніше: Block S., Hirt S. Foundations of Financial Management. — Homewood, Illinois: Irwin. — P. 449.

[231] Шарп У. Ф., Александер Г. Дж., Бэйли Дж. В. Инвестиции. — 1997. — С. 110.

[232] Див.: Copeland T., Weston I. F. Financial Theory and Corporate Policy Addison — Wesley, Reading M. A., 1983. або Samuels S. M., Wilkes F. M., Pragshaw R. E. Management of Company Finance. — L.: Chapman & Hall, 1993. — Р. 247.

[233] Тьюлз Р., Бредли Э., Тьюлз Т. Фондовый рынок. — С.533.

[234] Тьюлз Р., Бредли Э., Тьюлз Т. Фондовый рынок. — С.529—534.

[235] Шарп У. Ф., Александер Г. Дж., Бэйли Дж. В. Инвестиции. — 1997. — С. 531—533.

[236] Брейли Р., Майерс С. Принципы корпоративных финансов. — 1997. — С. 323—333.

[237] Брейли Р., Майерс С. Принципы корпоративных финансов. — 1997. — С. 332.

[238] Петерс Э. Хаос и порядок на рынках капитала. — М.: Мир, 2000. — С. 9.

[239] Там само. — С. 305.

[240] Кроновер Р. М. Фракталы и хаос в динамических системах / Пер. с анг. — М.: Постмаркет, 2000. — С. 11.

[241] Якимкин В. Н. Финансовый дилинг: книга 1. — М.: ИКФ Омега-Л, 2001. — С. 14.

[242] Цит. за кн.: Пайтген Х.-О., Рихтер П. Х. Красота фракталов. Образы комплексных динамических систем / Пер. с анг. — М.: Мир, 1993. — С. 3.

[243] Петерс Э. Хаос и порядок на рынках капитала. — М.: Мир, 2000. — С. 304.

[244] Там само. — С. 305.

[245] Петерс Э. Хаос и порядок на рынках капитала. — М.: Мир, 2000. — С.25.

[246] Селигмен Б. Основные течения современной экономической мысли / Пер. с англ. — М.: Прогресс, 1968. — С.270.

[247] Цит. за: Твид Л. Психология финансов / Пер. с англ. — М.: ИК «Аналитика», 2002. — С. 5.

[248] Якимкин В. Н. Финансовый дилинг: книга 1. — М.: ИКФ Омега-Л, 2001. — С. 4.

[249] Цит. за: Петерс Э. Хаос и порядок на рынках капитала. — М.: Мир, 2000. — С. 19.

[250] Петерс Э. Хаос и порядок на рынках капитала. — М.: Мир, 2000. — С. 19.

[251] Петерс Э. Хаос и порядок на рынках капитала. — М.: Мир, 2000. — С. 24.

[252] Там само.

[253] Твид Л. Психология финансов / Пер. с англ. — М.: ИК «Аналитика», 2002. — С. 55.

[254] Твид Л. Психология финансов / Пер. с англ. — М.: ИК «Аналитика», 2002. — С. 314.

[255] Цит. за: Петерс Э. Хаос и порядок на рынках капитала. — М.: Мир, 2000. — С. 235.

[256] Петерс Э. Хаос и порядок на рынках капитала. — М.: Мир, 2000. — С. 243—244.

[257] Там само.

[258] Твид Л. Психология финансов / Пер. с англ. — М.: ИК «Аналитика», 2002. — С. 72.

[259] Петерс Э. Хаос и порядок на рынках капитала. — М.: Мир, 2000. — С. 84.

[260] Якимкин В. Н. Финансовый дилинг: книга 1. — М.: ИКФ Омега-Л, 2001. — С. 32.

[261] Петерс Э. Хаос и порядок на рынках капитала. — М.: Мир, 2000. — С. 84.

[262] Там само. — С. 128.

[263] Петерс Э. Хаос и порядок на рынках капитала. — М.: Мир, 2000. — С. 128

[264] Дефоссе Г. Фондовая биржа и биржевые операции / Пер. с франц. — М.: «Церих-ПЭП», 1995. — С. 97.

Перша – пряма задача динаміки полягає в тому, що за заданими механічним рухом і масою точки визначають сили, під дією яких здійснюється цей рух.

Послідовність розв’язання першої задачі динаміки:

1. Показати на рисунку точку в обраній системі відліку в довільному положенні.

2. Показати на рисунку вектори активних сил, що діють на точку.

3. Умовно відкинути в’язі і замінити їх дію на точку силами, що дорівнюють відповідним реакціям в’язей, вектори яких також показати на рисунку.

4. Відповідно до обраної системи відліку, скласти динамічні диференціальні рівняння руху матеріальної точки.

5. Визначити за відомими кінематичними рівняннями руху точки проекції прискорення точки на осі координат обраної системи відліку і підставити їх у відповідні динамічні диференціальні рівняння руху.

6. Отримавши значення проекцій рівнодійної сили на координатні осі, знайти її величину і напрям за відповідними формулами.

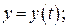
Нехай відомі маса точки та рівняння її руху в координатній формі 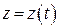. Необхідно визначити модуль і напрямок рівнодійної 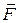сил, під впливом яких рухається матеріальна точка.

Розв’язання.

Двічі диференціюємо за часом кожне з рівнянь руху та отримуємо значення проекції прискорення точки на декартові осі координат

; ;

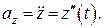
Підставивши значення проекцій прискорення на координатні осі до відповідних диференціальних рівнянь, дістанемо величини проекцій рівнодійної сили

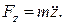
Модуль і напрям рівнодійної знаходимо за формулами

;

; ; .

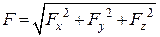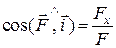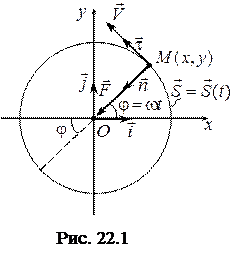Приклад. Точка масою m рухається у горизонтальній площині згідно рівнянь 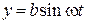відносно нерухомої прямокутної системи відліку 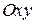(рис. 22.1); 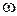і b - сталі величини. Визначити величину і напрямок рівнодійної сил 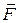, що діють на дану точку.

Розв’язання.

1. Знайдемо рівняннятраєкторії точки, вилучивши з рівнянь руху параметр t:

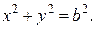
Отже, точка описує коло радіуса 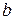з центром в початку координат.

2. Визначимо як змінюються проекції векторів швидкості та прискорення точки на кожну з координатних осей

; ;

; ,

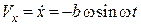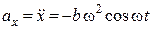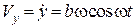звідки ; .

3. За диференціальними рівняннями руху матеріальної точки в декартових координатах знаходимо проекції рівнодійної на осі координат:

; .

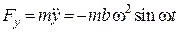4. Модуль та напрямок рівнодійної , під дією якої точка здійснює заданий рух, визначимо за формулами

;

;

.

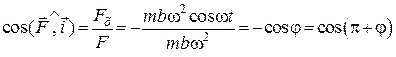Таким чином, кути, утворені вектором сили і напрямками координатних осей, змінюються за законами

.

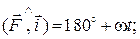
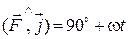Отже, вектор сталої за величиною сили 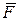, що діє на точку під час її руху, в кожний момент часу спрямований до нерухомого центра .

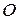Розв’язати цю задачу можна і, використовуючи динамічні рівняння руху матеріальної точки в натуральній формі в рухомій системі координат – дотичної з ортом 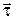і головної нормалі з ортом з центром в рухомій точці

або ,

оскільки 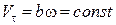, , 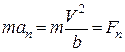тоді .

Напрямок вектора сили збігається з напрямком нормального прискорення, тобто спрямований до центра кола радіуса .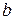

Друга – обернена задача динаміки полягає в тому, що за заданими силами, прикладеними до точки, її масою та початковими умовами визначають закон руху, який спричиняють ці сили.

План розв’язування другої (оберненої) задачі динаміки точки:

1. Показати на рисунку матеріальну точку в обраній системі відліку в довільний, але не початковий момент часу.

2. Показати вектори активних сил, що діють на матеріальну точку.

3. Подумки звільнити матеріальну точку від в’язей, замінюючи їх дію на точку силами, що дорівнюють реакціям в’язей, які також показати на рисунку.

4. Скласти динамічні диференціальні рівняння руху матеріальної точки в обраній системі відліку.

5. Двічі зінтегрувати кожне з динамічних диференціальних рівнянь руху та знайти загальні розв’язки задачі.

6. Скласти початкові умови руху за змістом конкретної задачі .

7. Визначити сталі інтегрування за складеними початковими умовами.

8. Підставити отримані значення сталих інтегрування до результату інтегрування та дістати шуканий закон руху матеріальної точки.

Нехай відомі сили, які діють на матеріальну точку, її маса , а також початкове положення точки та її початкова швидкість. Необхідно визначити кінематичні рівняння руху точки.

Будемо розв’язувати цю задачу за допомогою диференціальних рівнянь руху матеріальної точки в декартових координатах

; ; . (22.1)

Розв’язання цієї задачі зводиться до інтегрування трьох спільних диференціальних рівнянь (20.1) другого порядку відносно трьох невідомих функцій 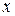, , , де незалежним аргументом є час . Загальні методи інтегрування цих рівнянь дотепер не розроблені. Але деякі прийоми побудови розв’язків системи диференціальних рівнянь (22.1) можна вказати.

Для розв’язування цієї задачі необхідно до кожного з рівнянь (22.1) підставити значення маси і суми проекцій на координатні осі сил, що діють на точку, а далі двічі зінтегрувати кожне з них за часом.

При цьому з’явиться шість невідомих сталих інтегрування, значення яких визначаються за початковими умовами: початковими координатами точки , , 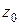і проекціями її початкової швидкості – , ,

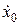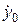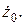
Підставляючи знайдені значення сталих інтегрування з умов задачі в отримані загальні розв’язки рівнянь (20.1), кінематичні рівняння руху точки набудуть такого вигляду:

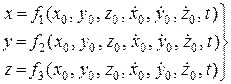(22.2)

У загальному випадку руху точки сили, що діють на неї, можуть бути як сталими, так і змінними в залежності від часу, швидкості та координат руху матеріальної точки.

22.3. Приклади розв’язання оберненої задачі динаміки матеріальної точки

Приклад І. Сила стала за модулем і напрямком.

1. Прямолінійний рух.

Розглянемо вільне падіння тіла з висоти 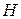, вважаючи вагу тіла сталою. Нехтуючи розмірами тіла, приймемо його за матеріальну точку. Силу опору повітря також не враховуємо.

Нехай матеріальна точка в деякий момент часу займає положення , яке знаходиться від початкового положення 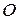на відстані (рис. 22.2). На точку в цьому положенні діє вертикальна сила ваги 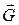. Спрямуємо вісь 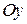вертикально вниз за траєкторією руху точки , обравши початок координат в її початковому положенні.

Запишемо другий закон Ньютона .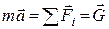

Диференціальне рівняння цього прямолінійного руху в обраній системі відліку має вигляд

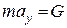або ,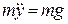

звідки

.

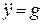Інтегруємо двічі за часом отримане рівняння ; .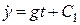

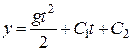Визначимо початкові умови. Нехай точка у початковий момент часу, знаходячись в точці відліку 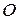, має початкову швидкість, яка дорівнює нулю. Тоді початкові умови виглядатимуть так: при : , .

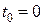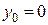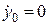Підставляючи початкові умови в отримані рівняння, визначимо значення сталих інтегрування

; .

Рівняння, що характеризує вільне падіння тіла у порожнечі, має вигляд

.

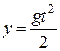Цей закон був вперше експериментально доведений Галілеєм.

Із закону вільного падіння, можна визначити час падіння тіла з певної висот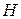и при , , 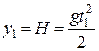звідки .

2. Криволінійний рух.

Розглянемо рух тіла, кинутого під кутом до горизонту, без урахування опору повітря. Вважаючи тіло матеріальною точкою, розглянемо його рух із початковою швидкістю 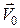, яка утворює кут 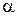згоризонтом. Початок відліку сполучимо з точкою вильоту тіла, спрямувавши вісь Ох вздовж горизонталі в бік руху, а вісь 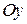– вгору (рис. 22.3).

Під час руху на тіло буде діяти тільки постійна сила ваги , яка спрямована вертикально вниз.

Запишемо основний закон динаміки точки, тобто другий закон Ньютона

.

Спроектувавши це векторне рівняння на координатні осі, отримаємо два диференціальні рівняння руху точки

; .

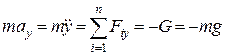Після перетворень рівняння матимуть вигляд: ;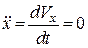

Інтегруємо послідовно за часом кожне з цих рівнянь і отримуємо загальний розв ’ язок задачі для проекцій вектора швидкості на координатні осі та рівняння руху точки

; ;

; .

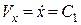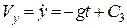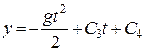Складемо початкові умови задачі при : , ;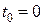

, .

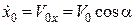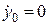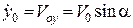Підставляючи ці значення в загальний розв'язок, дістанемо значення сталих інтегрування:

, , , .

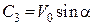Тоді проекції швидкості та рівняння руху точки для нашої задачі набудуть вигляду

;

; .

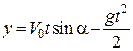Отримані рівняння дозволяють визначити час 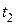і дальність польоту тіла 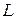, а також максимальну висоту його підйому .

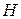Час польоту тіла можна визначити з четвертого рівняння; вважаючи, що в точці падіння тіла М₂ на Землю, координата 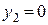, тоді

.

Підставивши значення 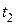у друге рівняння, знайдемо дальність польоту тіла: 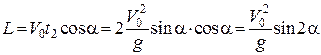,звідки .

Дальність польоту іншого тіла, за інших рівних умов, залежить від кута 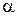і сягатиме максимуму, коли sin 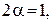тобто для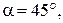

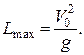
Із умови, що проекція швидкості у найвищій точці на вісь 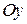дорівнює нулю, знайдемо час 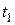польоту тіла до цієї точки

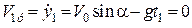, звідки .

Підставляючи значення 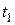до четвертого рівняння, отримаємо найбільшу висоту підйому тіла: , звідки .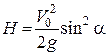

Приклад ІІ. Сила залежить від часу.

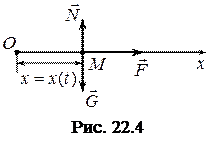Розглянемо рух матеріальної точки без початкової швидкості вздовж гладенької поверхні за горизонтальною прямою під впливом сили 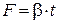, де

Виберемо початок відліку в точці 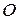, яка збігається з початковим положенням рухомої точки, і спрямуємо вісь 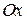вздовж траєкторії в бік руху точки (рис. 22.4).

Диференціальне рівняння руху отримаємо з основного закону динаміки точки

.

Проектуючи його на вісь 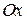, дістанемо

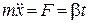або .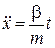

Інтегруємо двічі це рівняння

;

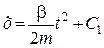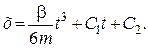
Підставивши початкові умови

при :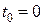

до результату інтегрування, маємо

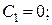
За таких значень сталих інтегрування закон руху точки та її швидкість відповідно мають вигляд

; .

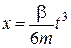Приклад ІІІ. Сила залежить від швидкості руху матеріальної точки.

Нехай тіло вагою 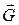рухається вниз без початкової швидкості із точки 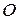, яку візьмемо за початок відліку (рис. 22.5). Вісь направимо вертикально вниз. Величина опору, який відчуває тіло, що падає, залежить від швидкості його руху. За невеликих значень швидкості, силу опору можна вважати пропорційною швидкості руху, а при великих значеннях швидкості, силу опору приймають пропорційною до квадрату швидкості точки. У даному прикладі розглянемо випадок, коли сила опору пропорційна швидкості та дорівнює , де 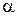– коефіцієнт пропорційності.

Оскільки тіло рухається поступально, розглядаємо його рух як рух матеріальної точки з такою самою масою.

Запишемо основне рівняння динаміки матеріальної точки, що рухається під впливом сил 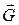і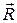

.

Проектуючи векторне рівняння на вісь 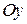, дістанемо диференціальне рівняння руху тіла

;

.

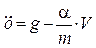Позначивши 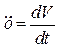і , запишемо отримане рівняння у вигляді

.

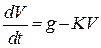Відокремивши змінні, одержимо

.

Введемо нову змінну 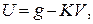тоді 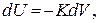звідки

Виконаємо заміну в рівнянні (20.3) та отримаємо

Інтегруючи це рівняння, дістанемо

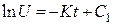або

Підставивши в це рівняння початкову умову

при

Дата добавления: 2014-12-25