
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Робота сили ваги 3 страница
|
|
|
|
знайдемо
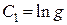 .
.
Тоді
 або
або 
Потенціюючи це рівняння, знайдемо:
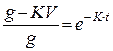 або
або 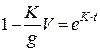 , звідки
, звідки
 .
.
Аналізуючи отримане рівняння, бачимо, що швидкість руху тіла весь час зростає, прагнучи до свого граничного значення, тобто
при 

Практично через деякий проміжок часу рух стає рівномірним. В цей момент сила опору середовища R дорівнюватиме вазі тіла. Тобто, враховуючи, що  , маємо
, маємо 

Запишемо рівняння (20.4) у вигляді

тоді
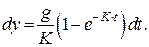
Після інтегрування це рівняння набуває вигляду
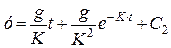 .
.
При 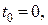 початкова умова:
початкова умова:  . Тоді стала інтегрування
. Тоді стала інтегрування
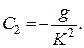
Підставивши значення  в результат інтегрування, дістанемо закон руху тіла, що падає з висоти
в результат інтегрування, дістанемо закон руху тіла, що падає з висоти 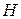 з врахуванням сили опору для нашого випадку
з врахуванням сили опору для нашого випадку

Якщо 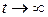 , то
, то  маємо практично лінійну залежність від часу за такого руху тіла:
маємо практично лінійну залежність від часу за такого руху тіла:
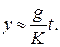
Приклад ІV. Сила залежить від положення точки.
 Розглянемо рух матеріальної точки
Розглянемо рух матеріальної точки  , кинутої вертикально вгору з поверхні Землі зі швидкістю
, кинутої вертикально вгору з поверхні Землі зі швидкістю  під впливом сили тяжіння Землі (рис. 22.6). Знайдемо залежність швидкості точки від її відстані до центру Землі.
під впливом сили тяжіння Землі (рис. 22.6). Знайдемо залежність швидкості точки від її відстані до центру Землі.
Виберемо початок координат у центрі Землі та спрямуємо вісь  вздовж траєкторії точки за напрямком руху. Як відомо, сила тяжіння
вздовж траєкторії точки за напрямком руху. Як відомо, сила тяжіння  обернено пропорційна квадрату відстані між точкою та центром Землі, тобто
обернено пропорційна квадрату відстані між точкою та центром Землі, тобто
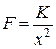 ,
,
де  – коефіцієнт пропорційності (рис. 22.6).
– коефіцієнт пропорційності (рис. 22.6).
Значення цього коефіцієнта легко визначити з умови, що на поверхні Землі в точці 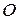 сила
сила  дорівнює силі ваги
дорівнює силі ваги
 ,
,
звідки

Остаточно формула сили тяжіння дорівнює
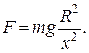
Запишемо диференціальне рівняння руху матеріальної точки

або
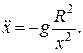
Перетворимо ліву частину цього рівняння
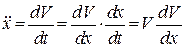 ,
,
тоді
 .
.
Відокремимо змінні в одержаному рівнянні та проінтегруємо обидві частини, вважаючи верхню границю змінною
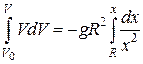 ,
,
звідки
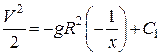 .
.
У початковий момент руху
при 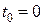 :
:  ,
, 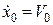 ;
;
|
|
|
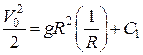 ,
,
тому
 .
.
Таким чином
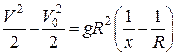 ,
,
звідки
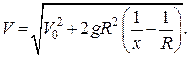
Максимальну відстань  , на яку піднімається тіло, можна отримати з цієї рівності при
, на яку піднімається тіло, можна отримати з цієї рівності при  .
.
Тоді після нескладних перетворень
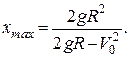
Із цієї формули видно, що  збільшується зі зростанням
збільшується зі зростанням  і, коли
і, коли  , відстань
, відстань 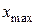 прагне до нескінченності. Отже, матеріальна точка, яку запустили з поверхні Землі зі швидкістю
прагне до нескінченності. Отже, матеріальна точка, яку запустили з поверхні Землі зі швидкістю  , вже не повернеться назад. Цю швидкість називають другою космічною швидкістю. Вона дорівнює
, вже не повернеться назад. Цю швидкість називають другою космічною швидкістю. Вона дорівнює
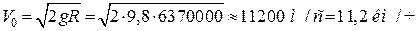 .
.
Лекція 23
ДИНАМІКА ВІДНОСНОГО РУХУ МАТЕРІАЛЬНОЇ ТОЧКИ
23.1. Диференціальні рівняння відносного руху матеріальної точки
Динамічні рівняння руху матеріальної точки в інерціальних системах відліку підпорядковуються законам Ньютона. Проте, в більшості випадків задачі динаміки зводяться до дослідження руху точки в неінерціальній системі відліку.
Звична для нас система, яка пов’язана з Землею, також не є інерціальною.
Другий закон Ньютона в неінерціальній системі відліку не виконується.
Розглянемо рух матеріальної точки відносно неінерціальної системи відліку.
Припустимо, що довільна матеріальна точка  рухається при дії рівнодійної активних сил
рухається при дії рівнодійної активних сил 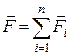 та рівнодійної реакцій в’язей
та рівнодійної реакцій в’язей  (рис. 23.1).
(рис. 23.1).
 При цьому точка
При цьому точка  рухається відносно рухомої системи координат
рухається відносно рухомої системи координат  , (відносний рух точки –
, (відносний рух точки –  ), яка,в свою чергу, рухається разом з точкою не поступально відносно нерухомої (інерціальної) системи координат
), яка,в свою чергу, рухається разом з точкою не поступально відносно нерухомої (інерціальної) системи координат 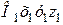 (переносний рух точки –
(переносний рух точки –  ).
).
Нехай, переносний рух рухомої системи координат  відносно нерухомої системи відліку
відносно нерухомої системи відліку 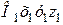 заданий. Визначимо відносний рух точки
заданий. Визначимо відносний рух точки  відносно рухомої системи координат
відносно рухомої системи координат  .
.
Абсолютний рух невільної точки  , масою
, масою  , відносно інерціальної системи координат
, відносно інерціальної системи координат 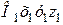 , тобто
, тобто 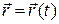 , підпорядковується другому закону Ньютона:
, підпорядковується другому закону Ньютона:
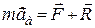 , (23.1)
, (23.1)
де 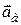 – абсолютне прискорення точки
– абсолютне прискорення точки  .
.
На підставі теореми Коріоліса, у випадку переносного непоступального руху, абсолютне прискорення точки 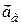 дорівнює геометричній сумі трьох прискорень – відносного
дорівнює геометричній сумі трьох прискорень – відносного 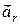 , переносного
, переносного  та прискорення Коріоліса
та прискорення Коріоліса  :
:
|
|
|
 . (23.2)
. (23.2)
Підставляючи значення (23.2) в (23.1), дістаємо векторне рівняння руху невільної матеріальної точки:
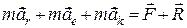 . (23.3)
. (23.3)
Перетворимо рівність (23.3) стосовно до відносного прискорення, тобто перенесемо два останніх доданка з лівої частини в праву:
 . (23.4)
. (23.4)
Введемо такі позначення:

 . (23.5)
. (23.5)
Вектор  називається силою інерції переносного руху.
називається силою інерції переносного руху.
Вектор 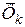 називається силою інерції Коріоліса.
називається силою інерції Коріоліса.
Підставляючи значення (23.5) в (23.4), отримаємо основне рівняння відносного руху матеріальної точки в векторній формі:
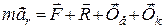 . (23.6)
. (23.6)
Таким чином, відносний рух матеріальноїточки можна розглядати як абсолютний, якщо до прикладених до точки активних сил та реакцій вязей умовно додати переносну 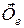 та коріолісову
та коріолісову  сили інерції.
сили інерції.
Розглянемо якісну відмінність між силами  і
і 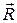 , прикладеними до точки
, прикладеними до точки  , і силами інерції
, і силами інерції 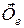 та
та  .
.
Сили  і
і 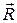 є результатом дії на матеріальну точку певних фізичних тіл, які можна повністю конкретно визначити в усіх окремих випадках.
є результатом дії на матеріальну точку певних фізичних тіл, які можна повністю конкретно визначити в усіх окремих випадках.
Джерела існування таких сил не залежать від вибору координатної системи. Ці сили називаються ньютоновимисилами.
Що стосується переносної 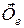 та коріолісової
та коріолісової  сил інерції, які називаються ейлеровими силами інерції, то вони з’являються лише тоді, коли матеріальна точка рухається в неінерціальній системі відліку і повністю залежать від характеру руху цієї системи відліку.
сил інерції, які називаються ейлеровими силами інерції, то вони з’являються лише тоді, коли матеріальна точка рухається в неінерціальній системі відліку і повністю залежать від характеру руху цієї системи відліку.
Ейлерові сили інерції не підкоряються закону рівності дії та протидії.
Якщо на деяку матеріальну точку діє сила інерції, то для неї не існує сили протидії, тобто ейлереві сили інерції не мають джерела свого виникнення з точки зору тверджень класичної механіки.
Крім того, значення ейлеревих сил інерції 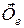 та
та  визначають не за допомогою приладів, як при визначенні фізичних ньютонових сил, а лише за формулами (23.5).
визначають не за допомогою приладів, як при визначенні фізичних ньютонових сил, а лише за формулами (23.5).
Отже, в межах класичної механіки ейлерові сили інерції 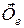 та
та  є фіктивними, тобто умовно прикладеними до матеріальної точки, рух якої розглядається.
є фіктивними, тобто умовно прикладеними до матеріальної точки, рух якої розглядається.
Переносна 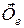 і кориолісова
і кориолісова  сили інерції не є відображенням механічної взаємодії матеріальних об’єктів, а є результатом формального зведення диференціальних рівнянь динаміки, записаних у неінерціальній системі відліку, до відомої форми запису диференціальних рівнянь в інерціальній системі відліку. Такий підхід дає змогу застосувати для розв’язання ряду практичних задач увесь розроблений раніше математичний апарат.
сили інерції не є відображенням механічної взаємодії матеріальних об’єктів, а є результатом формального зведення диференціальних рівнянь динаміки, записаних у неінерціальній системі відліку, до відомої форми запису диференціальних рівнянь в інерціальній системі відліку. Такий підхід дає змогу застосувати для розв’язання ряду практичних задач увесь розроблений раніше математичний апарат.
|
|
|
Якщо спроектувати обидві частини векторного рівняння (23.6) на рухомі координатні осі Охуz, отримаємо диференціальні рівняння відносного руху матеріальної точки:
 ;
;

 . (23.7)
. (23.7)
23.2. Принцип відносності в класичній механіці
Розглянемо частинний випадок, коли рухома координатна система Охуz рухається відносно нерухомої  поступально, прямолінійно і рівномірно, тобто
поступально, прямолінійно і рівномірно, тобто 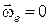 і
і 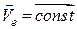 . В цьому випадку
. В цьому випадку  ,
,  і тому відповідно:
і тому відповідно: 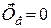 і
і  .
.
Отже, основне рівняння (23.6) відносного руху точки має вигляд:
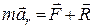 . (23.8)
. (23.8)
Порівнюючи рівняння (23.1) і (23.8) бачимо, що в цьому частинному випадку, абсолютний і відносний рухи точки  визначаються ідентичними рівняннями. Тобто, рухома координатна система
визначаються ідентичними рівняннями. Тобто, рухома координатна система  також є інерціальною.
також є інерціальною.
Таким чином, всі системи відліку, що рухаються рівномірно й прямолінійно відносно інерціальної координатної системи, теж є інерціальними, а рух матеріальної точки відносно будь-якої з них можнарозглядати як абсолютний рух.
Це вказує на інваріантність рівнянь динаміки при переході від однієї інерціальної системи відліку до іншої.
Якщо уявити спостерігача в закритому приміщенні, яке рухається рівномірно і прямолінійно, то він, не відчуваючи дії переносної і коріолісової сил інерції, не може визначити свого положення відносно інших систем відліку, отже не може визначити, чи рухається його система відліку чи перебуває в стані спокою.
Таким чином, приходимо до висновку, який носить назву принципу відносності в класичній механіці: жодними механічними дослідженнями в середовищі не можна визначити його рівномірного і прямолінійного руху.
23.3. Випадок відносного спокою. Сила ваги
Нехай точка  перебуває в стані відносного спокою, тобто
перебуває в стані відносного спокою, тобто 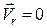 і
і  . У цьому разі прискорення Коріоліса, а тому і сила інерції Коріоліса, дорівнюють нулю (
. У цьому разі прискорення Коріоліса, а тому і сила інерції Коріоліса, дорівнюють нулю (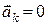 ,
,  ).
).
Тоді рівняння відносного спокою матеріальної точки має вигляд:
 . (23.9)
. (23.9)
Отже, у випадку, коли матеріальна точка перебуває у стані відносного спокою, геометрична сума прикладених до неї активних сил, реакцій вязей і переносної сили інерції дорівнює нулю.
|
|
|
Як приклад розглянемо відносний спокій матеріальної точки  на поверхні Землі (рис. 23.2).
на поверхні Землі (рис. 23.2).
 Скористаємось рівнянням відносного спокою точки, яка в цьому разі є невільною. Застосуємо принцип звільнення від в’язей: Тоді рівняння (21.9) набуває вигляду:
Скористаємось рівнянням відносного спокою точки, яка в цьому разі є невільною. Застосуємо принцип звільнення від в’язей: Тоді рівняння (21.9) набуває вигляду:
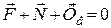 . (23.10)
. (23.10)
Тут – сила тяжіння точки біля поверхні Землі;  – реакція опори;
– реакція опори; 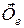 – переносна сила інерції точки. За величиною, сила
– переносна сила інерції точки. За величиною, сила  , згідно із законом тяжіння, дорівнює:
, згідно із законом тяжіння, дорівнює:
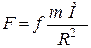 ;
;
де  – гравітаційна стала;
– гравітаційна стала;  – маса точки;
– маса точки;  – маса Землі, а
– маса Землі, а 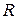 – її радіус; сили інерції
– її радіус; сили інерції
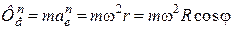 ;
;
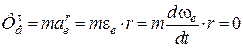 ,
,
оскільки  .
.
Очевидно, сила тиску точки  на Землю
на Землю  буде дорівнювати:
буде дорівнювати:
 .
.
Отже, сила 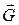 що є рівнодійною сили тяжіння
що є рівнодійною сили тяжіння  і переносної сили інерції
і переносної сили інерції 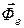 ,називається силою ваги і дорівнює їх геометричній сумі:
,називається силою ваги і дорівнює їх геометричній сумі:
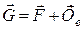 . (23.11)
. (23.11)
Напрям сили ваги визначає напрям вертикалі в даній точці поверхні Землі. Напрям і величину реакції поверхні Землі 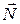 визначаємо виходячи з величини і напрямку сили ваги
визначаємо виходячи з величини і напрямку сили ваги 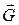 (рис. 23.2).
(рис. 23.2).
Найбільшу вагу тіло має на полюсі, де  , а сила
, а сила  – максимальне значення (тут радіус Землі мінімальний), а найменшу вагу – на екваторі.
– максимальне значення (тут радіус Землі мінімальний), а найменшу вагу – на екваторі.
За допомогою теорії відносного руху точки пояснюється тиск потяга на рейки; дія води в річках на їх русла, стан невагомості тіла, рух маятника Фуко і т. д.
23.4. Приклади розв’язування задач динаміки відносного руху матеріальної точки
 Приклад 1. Точка
Приклад 1. Точка 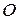 підвісу математичного маятника рухається вниз зі сталим прискоренням
підвісу математичного маятника рухається вниз зі сталим прискоренням  . Знайти період малих коливань маятника, якщо
. Знайти період малих коливань маятника, якщо 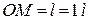 (рис. 23.3).
(рис. 23.3).
Розв’язання. Маятник перебуває в складному русі.
Переносний рух – це поступальний прискорений рух маятника разом з точкою привісу 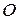 вздовж вертикалі вниз.
вздовж вертикалі вниз.
Відносним рухом є рух точки  за дугою кола радіуса
за дугою кола радіуса 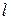 .
.
Покажемо сили, які діють на точку  (рис. 23.3). Отже, це вага
(рис. 23.3). Отже, це вага 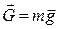 і реакція мотузки
і реакція мотузки  , а також умовно прикладені
, а також умовно прикладені  і
і  сили інерції.
сили інерції.
Запишемо векторне рівняння відносно руху точки  :
:
 .
.
Оскільки переносний рух – поступальний  , то прискорення Кориоліса
, то прискорення Кориоліса  і відповідно сила інерції Кориоліса
і відповідно сила інерції Кориоліса  дорівнюють нулю.
дорівнюють нулю.
Переносна сила інерції  спрямована до гори:
спрямована до гори:
 .
.
Спроектуємо векторне рівняння на дотичну до відносної траєкторії точки  :
:
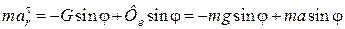 .
.
Проекція реакції в’язі нитки  на дотичну дорівнює нулю.
на дотичну дорівнює нулю.
Проекція відносного прискорення 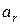 на дотичну за модулем дорівнює:
на дотичну за модулем дорівнює:

З урахуванням малих коливань приймаємо  . Отже, рівняння відносного руху має вигляд:
. Отже, рівняння відносного руху має вигляд:
 ;
;
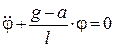 .
.
Тут
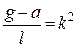 .
.
Період малих коливань маятника дорівнює:
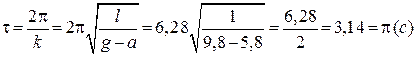 .
.
Приклад 2. Гладенький стержень  довжиною
довжиною 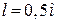 обертається рівномірно навколо вертикальної осі, що проходить через його кінець зі сталою кутовою швидкістю
обертається рівномірно навколо вертикальної осі, що проходить через його кінець зі сталою кутовою швидкістю  (рис. 23.4). Вздовж стержня вільно переміщується кільце
(рис. 23.4). Вздовж стержня вільно переміщується кільце  , яке в початковий момент часу (
, яке в початковий момент часу (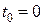 ) знаходилось в середині стержня. Через скільки секунд кільце зійде зі стержня?
) знаходилось в середині стержня. Через скільки секунд кільце зійде зі стержня?
Розв’язання. Кільце М здійснює складний рух: поступальний вздовж стержняі переносний – обертальний разом із стержнем навколо нерухомої вертикальної осі 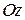 .
.
Рухому систему відліку Ох пов’язуємо зі стержнем  .
.
До кільця прикладені: сила ваги 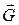 , вертикальна
, вертикальна 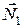 та горизонтальна
та горизонтальна 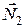 складові повної реакції стержня. Умовно прикладаємо сили інерції
складові повної реакції стержня. Умовно прикладаємо сили інерції 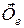 і
і  , які за модулем дорівнюють:
, які за модулем дорівнюють:

 ;
;
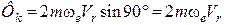 .
.
Векторне рівняння відносного руху кільця М запишемо у такому вигляді:
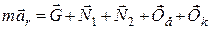 .
.
Спроектуємо його на вісь 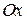 . Вектори
. Вектори 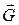 ,
, 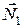 ,
, 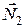 та
та 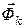 перпендикулярні
перпендикулярні 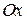 (рис. 21.4).
(рис. 21.4).
Отримаємо диференціальне рівняння відносного руху кільця  :
:
 ;
;  ,
,
звідки
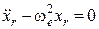 .
.
Складемо характеристичне рівняння:

корені якого
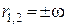 .
.
Тоді, загальний розв’язок рівняння матиме вигляд:
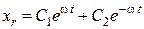 .
.
Для визначення сталих інтегрування  і
і  запишемо вираз для швидкості кільця:
запишемо вираз для швидкості кільця:
 .
.
та складемо початкові умови:
при 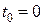 :
: 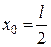 ,
, 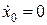 .
.
Підставляючи їх у рівняння руху і швидкості, відповідно отримуємо:
|
|
|
|
|
Дата добавления: 2014-12-25; Просмотров: 427; Нарушение авторских прав?; Мы поможем в написании вашей работы!