Другие элементы меню 6 страница

Определение 3 (инварианта цикла) Предикат Inv(x, z) называется инвариантом цикла while, если истинна следующая триада Хоара:

{ Inv(x, z)& B }S(x,z){ Inv(x,z) }

Содержательно это означает, что из истинности инварианта цикла до начала выполнения тела цикла, и из истинности условия цикла, гарантирующего выполнение тела, следует истинность инварианта после выполнения тела цикла. Сколь много раз не выполнялось бы тело цикла, его инвариант остается истинным.

Для любого цикла можно написать сколь угодно много инвариантов. Любое тождественное условие (2*2 =4) является инвариантом любого цикла. Поэтому среди инвариантов выделяются так называемые подходящие инварианты цикла. Они называются подходящими, поскольку позволяют доказать корректность цикла по отношению к его пред и постусловиям. Как доказать корректность цикла? Рассмотрим соответствующую триаду:

{ Pre(x) } Init(x,z); while(B)S(x,z);{ Post(x,z) }

Доказательство разбивается на три этапа. Вначале доказываем истинность триады:

(*) { Pre(x) } Init(x,z){ RealInv(x,z) }

Содержательно это означает, что предикат RealInv становится истинным после выполнения инициализирующей части. Далее доказывается, что RealInv является инвариантом цикла:

(**) { RealInv (x, z)& B} S(x,z){ RealInv (x,z)}

На последнем шаге доказывается, что наш инвариант обеспечивает решение задачи после завершения цикла:

(***) ~B & RealInv (x, z) –> Post(x,z)

Это означает, что из истинности инварианта и условия завершения цикла следует требуемое постусловие.

Определение 4 (подходящего инварианта) Предикат RealInv, удовлетворяющий условиям (*), (**), (***)называется подходящим инвариантом цикла.

С циклом связано еще одно важное понятие – варианта цикла, используемое для доказательства завершаемости цикла.

Определение 5 (варианта цикла) Целочисленное неотрицательное выражение Var(x, z) называется вариантом цикла, если выполняется следующая триада:

{(Var(x,z)= n) & B } S(x,z){(Var(x,z) = m) & (m < n)}

Содержательно это означает, что каждое выполнение тела цикла приводит к уменьшению значения его варианта. После конечного числа шагов вариант достигает своей нижней границы и цикл завершается. Простейшим примером варианта цикла является выражение n-i для цикла for(i=1; i<=n; i++) S(x, z);.

Пользоваться инвариантами и вариантами цикла нужно не только и не столько для того, чтобы проводить формальное доказательство корректности циклов. Они способствуют написанию корректных циклов. Правило корректного программирования гласит: «При написании каждого цикла программист должен определить его походящий инвариант и вариант». Задание предусловий, постусловий, вариантов и инвариантов циклов является такой же частью работы по разработке корректного метода, как и написание самого кода.

Рекурсия

Рекурсия является одним из наиболее мощных средств в арсенале программиста. Рекурсивные структуры данных и рекурсивные методы широко используются при построении программных систем. Рекурсивные методы как правило являются наиболее подходящими при работе с рекурсивными структурами данных – списками, деревьями. Рекурсивные методы обхода деревьев являются классическим примером.

Определение 6 (рекурсивного метода): Метод P (процедура или функция) называется рекурсивным, если при выполнении тела метода происходит вызов метода P.

Рекурсия может быть прямой, если вызов P происходит непосредственно в теле метода P. Рекурсия может быть косвенной, если в теле P вызывается метод Q (эта цепочка может быть продолжена), в теле которого вызывается метод P. Определения методов P и Q взаимно рекурсивны, если в теле метода Q вызывается метод P, вызывающий, в свою очередь, метод Q.

Для того чтобы рекурсия не приводила к зацикливанию, в тело нормального рекурсивного метода всегда встраивается оператор выбора, одна из ветвей которого не содержит рекурсивных вызовов. Если в теле рекурсивного метода рекурсивный вызов встречается только один раз, то это явный признак того, что рекурсию можно заменить обычным циклом, что приводит к более эффективной программе, поскольку реализация рекурсии требует временных затрат и работы со стековой памятью. Приведу вначале простейший пример рекурсивного определения функции, вычисляющей факториал целого числа:

public long factorial(int n)

{

if (n<=1) return (1);

else return (n*factorial(n-1));

}// factorial

Функция factorial является примером прямого рекурсивного определения – в ее теле она сама себя вызывает. Здесь, как и положено, есть нерекурсивная ветвь, завершающая вычисления, когда n становится равным 1. Это пример так называемой «хвостовой» рекурсии, когда в теле встречается ровно один рекурсивный вызов, стоящий в конце соответствующего выражения. Хвостовую рекурсию намного проще записать в виде обычного цикла. Вот циклическое определение той же функции:

public long fact(int n)

{

long res =1;

for(int i = 2; i <=n; i++) res*=i;

return(res);

}// fact

Конечно циклическое определение проще, понятнее и эффективнее, применять рекурсию в подобных ситуациях не следует. Интересно сравнить время вычислений, дающее некоторое представление о том, насколько эффективно реализуется рекурсия. Вот соответствующий тест, решающий эту задачу:

public void TestTailRec()

{

Hanoi han = new Hanoi(5);

long time1, time2;

long f=0;

time1 = getTimeInMilliseconds();

for (int i = 1; i <1000000; i++)f =han.fact(15);

time2 =getTimeInMilliseconds();

Console.WriteLine(" f= {0}, " +

"Время работы циклической процедуры: {1}",f,time2 -time1);

time1 = getTimeInMilliseconds();

for (int i = 1; i <1000000; i++)f =han.factorial(15);

time2 =getTimeInMilliseconds();

Console.WriteLine(" f= {0}, " +

"Время работы рекурсивной процедуры: {1}",f,time2 -time1);

}

Каждая из функций вызывается в цикле, работающем 1000000 раз. До начала цикла и после его окончания вычисляется текущее время. Разность этих времен и дает оценку времени работы функций. Обе функции вычисляют факториал числа 15.

Проводить сравнение эффективности работы различных вариантов – это частый прием, используемый при разработке программ. И я им буду пользоваться неоднократно. Встроенный тип DateTime обеспечивает необходимую поддержку для получения текущего времени. Он совершенно необходим, когда приходится работать с датами. Я не буду подробно описывать его многочисленные статические и динамические методы и свойства. Ограничусь лишь приведением функции, которую я написал для получения текущего времени, измеряемого в миллисекундах. Статический метод Now класса DateTime возвращает объект этого класса, соответствующий дате и времени в момент создания объекта. Многочисленные свойства этого объекта позволяют извлечь требуемые характеристики. Приведу текст функци getTimeInMilliseconds:

long getTimeInMilliseconds()

{

DateTime time = DateTime.Now;

return (((time.Hour*60 + time.Minute)*60 + time.Second)*1000

+ time.Millisecond);

}

Результаты измерений времени работы рекурсивного и циклического вариантов функций слегка отличаются от запуска к запуску, но порядок остается одним и тем же. Эти результаты показаны на рис. 10.1.

Рис. 10.1. Сравнение времени работы циклической и рекурсивной функций

Вовсе не обязательно, чтобы рекурсивные методы работали медленнее нерекурсивных методов. Классическим примером являются методы сортировки. Известно, что время работы нерекурсивной пузырьковой сортировки имеет порядок c*n² , где c – некоторая константа. Для рекурсивной процедуры сортировки слиянием время работы – q*n*log(n), где q – константа. Понятно, что для больших n сортировка слиянием работает быстрее независимо от соотношения значений констант. Сортировка слиянием хороший пример применения рекурсивных методов. Она демонстрирует известный прием, называемый «разделяй и властвуй». Его суть в том, что исходная задача разбивается на подзадачи меньшей размерности, допускающие решение тем же алгоритмом. Решения отдельных подзадач затем объединяются, давая решение исходной задачи. В задаче сортировки исходный массив размерности n можно разбить на два массива размерности n/2, для каждого из которых рекурсивно вызывается метод сортировки слиянием. Полученные отсортированные массивы сливаются в единый массив с сохранением упорядоченности.

На примере сортировки слиянием покажем, как можно оценить время работы рекурсивной процедуры. Обозначим через T(n) время работы процедуры на массиве размерности n. Учитывая, что слияние можно выполнить за линейное время, справедливо следующее соотношение:

T(n) = 2T(n/2) + cn

Предположим для простоты, что n задается степенью числа 2, то есть n = 2^k. Тогда наше соотношение имеет вид:

T(2^k) = 2T(2^k-1) + c2^k

Полагая, что T(1) =c, путем несложных преобразований, используя индукцию, можно получить окончательный результат:

T(2^k) = c*k*2^k = c*n*log(n)

Известно, что это лучшее по порядку время решения задачи сортировки. Когда исходную задачу удается разделить на подзадачи одинаковой размерности, то при условии существования линейного алгоритма слияния, рекурсивный алгоритм имеет аналогичный порядок сложности. К сожалению, не всегда удается исходную задачу разбить на k подзадач одинаковой размерности n/k. Часто такое разбиение не представляется возможным.

Рекурсивное решение задачи «Ханойские башни»

Рассмотрим известную задачу о конце света – Ханойские башни. Ее содержательная постановка такова. В одном из буддийских монастырей монахи уже тысячу лет занимаются перекладыванием колец. Они располагают тремя пирамидами, на которых надеты кольца разных размеров. В начальном состоянии 64 кольца были надеты на первую пирамиду, упорядоченные по размеру. Монахи должны переложить все кольца с первой пирамиды на вторую, выполняя единственное условие – кольцо нельзя положить на кольцо меньшего размера. При перекладывании можно использовать все три пирамиды. Монахи перекладывают одно кольцо за одну секунду. Как только они закончат свою работу, наступит конец света.

Беспокоиться о близком конце света не стоит. Задача эта не под силу и современным компьютерам. Число ходов в ней равно 2⁶⁴, а это, как известно, большое число и компьютер, работающий в сотню миллионов раз быстрее монахов, не справится с этой задачей в ближайшие тысячелетия.

Рассмотрим эту задачу в компьютерной постановке. Я спроектировал класс Hanoi, в котором роль пирамид играют три массива, а числа играют роль колец. Вот описание данных этого класса и некоторых его методов:

public class Hanoi

{

int size,moves;

int[] tower1, tower2,tower3;

int top1,top2,top3;

Random rnd = new Random();

public Hanoi(int size)

{

this.size = size;

tower1 = new int[size];

tower2 = new int[size];

tower3 = new int[size];

top1 = size; top2=top3=moves =0;

}

public void Fill()

{

for (int i =0; i< size; i++)

tower1[i]=size-i;

}

}//Hanoi

Массивы tower играют роль ханойских башен, связанные с ними переменные top задают вершину – первую свободную ячейку при перекладывании колец (чисел). Переменная size задает размер массивов (число колец), а переменная moves используется для подсчета числа ходов. Для дальнейших экспериментов нам понадобится генерирование случайных чисел, поэтому в классе определен объект уже известного нам класса Random (см. лекция 7). Конструктор класса инициализирует поля класса, а метод Fill формирует начальное состояние, задавая для первой пирамиды числа, идущие в порядке убывания к ее вершине (top).

Займемся теперь непосредственно методом, реализующим нашу игру и занимающимся перекладыванием колец в соответствии с правилами игры. Заметьте, написать нерекурсивный вариант ханойских башен совсем не просто. Можно конечно написать цикл, завершающийся по достижению требуемой конфигурации, на каждом шаге которого выполняется очередной ход. Но даже первый ход не тривиален. Поскольку фиксирована пирамида, где должны быть собраны кольца, то неясно, куда нужно переложить первое кольцо – на вторую или третью пирамиду?

Рекурсивный вариант решения задачи прозрачен, хотя и напоминает некоторый род фокуса, что характерно для рекурсивного стиля мышления. Базис рекурсии прост. Для перекладывания одного кольца задумываться о решении не нужно – оно дается в один ход. Если есть базисное решение, то оставшаяся часть также очевидна. Нужно применить рекурсивно алгоритм, переложив n-1 кольцо с первой пирамиды на третью пирамиду. Затем сделать очевидный ход, переложив последнее самое большое кольцо с первой пирамиды на вторую. Затем снова применить рекурсию, переложив n-1 кольцо с третьей пирамиды на вторую пирамиду. Задача решена. Столь же проста ее запись на языке программирования:

public void HanoiTowers()

{

HT(ref tower1, ref tower2, ref tower3,

ref top1, ref top2, ref top3,size);

Console.WriteLine("\nВсего ходов 2^n -1 = {0}",moves);

}

Как обычно в таких случаях, вначале пишется нерекурсивная процедура, вызывающая рекурсивный вариант с аргументами. В качестве фактических аргументов процедуре HT передаются поля класса, обновляемые в процессе многочисленных рекурсивных вызовов и потому снабженные ключевым словом ref. Рекурсивный вариант реализует описанную выше идею алгоритма:

/// <summary>

/// Перенос count колец с tower1 на tower2, соблюдая правила и

/// используя tower3. Свободные вершины башен - top1, top2, top3

/// </summary>

void HT(ref int [] t1, ref int [] t2, ref int [] t3,

ref int top1, ref int top2, ref int top3, int count)

{

if (count == 1)Move(ref t1, ref t2, ref top1, ref top2);

{

HT(ref t1, ref t3, ref t2, ref top1, ref top3, ref top2,count-1);

Move(ref t1, ref t2, ref top1, ref top2);

HT(ref t3, ref t2, ref t1, ref top3, ref top2, ref top1,count-1);

}

}// HT

Процедура Move описывает очередной ход. Ее аргументы однозначно задают, с какой и на какую пирамиду нужно перенести кольцо. Никаких сложностей в ее реализации нет.

void Move(ref int []t1, ref int [] t2, ref int top1, ref int top2)

{

t2[top2] = t1[top1-1];

top1--; top2++; moves++;

//PrintTowers();

}// Move

Метод PrintTowers позволяет проследить, за ходом переноса. Приведу еще метод класса Testing, тестирующий работу по переносу колец:

public void TestHanoiTowers()

{

Hanoi han = new Hanoi(10);

Console.WriteLine("Ханойские башни");

han.Fill();

han.PrintTowers();

han.HanoiTowers();

han.PrintTowers();

}

На рис. 10.2 показаны результаты работы с включенной печатью каждого хода для случая переноса трех колец.

Рис. 10.2. Ханойские башни

В рекурсивном варианте исчезли все трудности, связанные с выбором хода, соблюдением правил. Они выполняются почти автоматически, поскольку слияние частных решений не нарушает правил. В этом еще одна мощь рекурсии.

Решение исходной задачи свелось к решению двух подзадач и одному ходу. В отличие от задачи сортировки слиянием обе подзадачи имеют не половинный размер, а размер лишь на 1 меньше исходного. Это, казалось бы, незначительное изменение приводит к серьезным потерям эффективности вычислений. Если сложность в первом случае имела порядок n*log(n), то теперь она становится экспоненциальной. Давайте проведем анализ временных затрат для ханойских башен (и всех задач, сводящихся к решению двух подзадач размерности n-1). Подсчитаем требуемое число ходов T(n). С учетом структуры решения:

T(n) = 2T(n-1) +1

Простое доказательство по индукции дает:

T(n) = 2^n-1 + 2^n-2 + … + 2 +1 = 2ⁿ -1

Можно показать, что последовательность ходов, реализуемая рекурсивным алгоритмом, является оптимальной, так что никакой другой алгоритм не может решить задачу за меньшее число ходов.

Быстрая сортировка Хоара

Продолжая тему рекурсии, познакомимся с реализацией на C# еще одного известного рекурсивного алгоритма, применяемого при сортировке массивов. Описанный ранее рекурсивный алгоритм сортировки слиянием имеет один существенный недостаток – для слияния двух упорядоченных массивов за линейное время необходима дополнительная память. Разработанный Ч. Хоаром метод сортировки, получивший название быстрого метода сортировки – QuickSort, не требует дополнительной памяти. Хотя этот метод и не является самым быстрым во всех случаях, но он обеспечивает на практике хорошие результаты. Нужно отметить, что именно этот метод сортировки встроен в класс System.Array.

Идея алгоритма быстрой сортировки состоит в том, чтобы выбрать в исходном массиве некоторый элемент M, затем в начальной части массива собрать все элементы, меньшие M. Так появляются две подзадачи размерности k и n-k, к которым рекурсивно применяется алгоритм. Если в качестве элемента M выбирать медиану сортируемой части массива, то обе подзадачи имели бы одинаковый размер, и алгоритм быстрой сортировки был бы оптимальным по времени работы. Но расчет медианы требует своих затрат времени и усложняет алгоритм. Поэтому обычно элемент M выбирается случайным образом, в этом случае быстрая сортировка оптимальна лишь в среднем, а для плохих вариантов (когда в качестве M всякий раз выбирается минимальный элемент) имеет порядок n².

Несмотря на простоту идеи, алгоритм сложен в своей реализации, поскольку весь построен на циклах и операторах выбора. Я проводил построение алгоритма параллельно с обоснованием его корректности, введя инварианты соответствующих циклов. Текст обоснования встроен в текст метода. Приведу его, а затем дам некоторые комментарии. Вначале, как обычно приведу нерекурсивную процедуру, вызывающую рекурсивный метод:

/// <summary>

/// Вызывает рекурсивную процедуру QSort,

/// передавая ей границы сортируемого массива.

/// Сортируемый массив tower1 задается

/// соответствующим полем класса.

public void QuickSort()

{

QSort(0,size-1);

}

Вот чистый текст рекурсивной процедуры быстрой сортировки Хоара:

void QSort(int start, int finish)

{

if (start!= finish)

{

int ind = rnd.Next(start,finish); int item = tower1[ind];

int ind1 = start, ind2 = finish; int temp;

while (ind1 <=ind2)

{

while ((ind1 <=ind2)&& (tower1[ind1] < item)) ind1++;

while ((ind1 <=ind2)&&(tower1[ind2] >= item)) ind2--;

if (ind1 < ind2)

{

temp = tower1[ind1]; tower1[ind1] = tower1[ind2];

tower1[ind2] = temp; ind1++; ind2--;

}

}

if (ind1 == start)

{

temp = tower1[start]; tower1[start] = item; tower1[ind] = temp;

QSort(start+1,finish);

}

{

QSort(start,ind1-1); QSort(ind2+1, finish);

}

}

}// QuickSort

Проведите эксперимент – закройте книгу и попробуйте написать эту процедуру самостоятельно. Если вам удастся сделать это без ошибок и она пройдет у вас с первого раза, то вы – блестящий программист и вам нужно читать другие книги. Я полагаю, что в таких процедурах ошибки неизбежны, для их исправления требуется серьезная отладка. Полагаю также, что помимо обычного тестирования полезно применять обоснование корректности, основанное на предусловиях и постусловиях, инвариантах цикла. Проектируя эту процедуру, я параллельно встраивал обоснование ее корректности. Это не строгое доказательство, но, дополняя тестирование, оно достаточно, чтобы автор поверил в корректность процедуры и представил ее на суд зрителей, как это сделал я.

/// <summary>

/// Небольшая по размеру процедура содержит три

/// вложенных цикла while, два оператора if и рекурсивные

/// вызовы. Для таких процедур задание инвариантов и

/// обоснование корректности облегчает отладку.

/// </summary>

/// <param name="start"> начальный индекс сортируемой части

/// массива tower </param>

/// <param name="finish"> конечный индекс сортируемой части

/// массива tower </param>

/// Предусловие: (start <= finish)

/// Постусловие: массив tower отсортирован по возрастанию

void QSort(int start, int finish)

{

if (start!= finish)

//если (start = finish), то процедура ничего не делает,

//но постусловие выполняется, поскольку массив из одного

//элемента отсортирован по определению.

//Докажем истинность постусловия для массива с числом элементов >1.

{

int ind = rnd.Next(start,finish);

int item = tower1[ind];

int ind1 = start, ind2 = finish;

int temp;

/********

Введем три непересекающихся множества:

S1: {tower1(i), start <= i =< ind1-1}

S2: {tower1(i), ind1 <= i =< ind2}

S1: {tower1(i), ind2+1 <= i =< finish}

Введем следующие логические условия,

играющие роль инвариантов циклов нашей программы:

P1: объединение S1, S2, S3 = tower1

P2: (S1(i) < item) Для всех элементов S1

P3: (S3(i) >= item) Для всех элементов S3

P4: item - случайно выбранный элемент tower1

Нетрудно видеть, что все условия становятся

истинными после завершения инициализатора цикла.

Для пустых множеств S1 и S3 условия P2 и P3

считаются истинными по определению.

Inv = P1 & P2 & P3 & P4

********/

while (ind1 <=ind2)

{

while ((ind1 <=ind2)&& (tower1[ind1] < item)) ind1++;

//(Inv == true) & ~B1 (B1 - условие цикла while)

while ((ind1 <=ind2)&&(tower1[ind2] >= item)) ind2--;

//(Inv == true) & ~B2 (B2 - условие цикла while)

if (ind1 < ind2)

//Из Inv & ~B1 & ~B2 & B3 следует истинность:

//((tower1[ind1] >= item)&&(tower1[ind2]<item))== true

//Это условие гарантирует, что последующий обмен элементов

//обеспечит выполнение инварианта Inv

{

temp = tower1[ind1]; tower1[ind1] = tower1[ind2];

tower1[ind2] = temp;

ind1++; ind2--;

}

//(Inv ==true)

}

//из условия окончания цикла следует: (S2 - пустое множество)

if (ind1 == start)

//В этой точке S1 и S2 - это пустые множества, -> (S3 = tower1)

//Нетрудно доказать, что отсюда следует истинность:(item = min)

//Как следствие, можно минимальный элемент сделать первым,

// а к оставшемуся множеству применить рекурсивный вызов.

{

temp = tower1[start]; tower1[start] = item;

tower1[ind] = temp;

QSort(start+1,finish);

}

//Здесь оба множества S1 и S3 не пусты.

//К ним применим рекурсивный вызов.

{

QSort(start,ind1-1);

QSort(ind2+1, finish);

}

//Индукция по размеру массива и истинность инварианта

//доказывает истинность постусловия в общем случае.

}

}// QuickSort

Приведу некоторые комментарии к этому доказательству. Задание предусловия и постусловия процедуры QSort достаточно очевидно – сортируемый массив должен быть не пустым, а после работы метода должен быть отсортированным. Важной частью обоснования является четкое введение трех множеств S1, S2, S3 и условий, накладываемых на их элементы. Эти условия и становятся частью инварианта, сохраняющегося при работе различных циклов нашего метода. Вначале множества S1 и S3 пусты, в ходе вычислений пустым становится множество S2. так происходит формирование подзадач, к которым рекурсивно применяется алгоритм. Особым представляется случай, когда множество S1 тоже пусто. Нетрудно показать, что такая ситуация возможна только в том случае, если случайно выбранный элемент множества, служащий критерием разбиения исходного множества на два подмножества, является минимальным элементом.

Почему обоснование полезно практически? Дело в том, что в данном алгоритме приходится следить за границами множеств (чтобы они не пересекались), за пустотой множеств (служащих условием окончания циклов), за выполнением условий, накладываемых на элементы множеств. Если явно не ввести эти понятия, то вероятность ошибки существенно возрастает. В заключение следует все-таки привести результат сортировки хотя бы одного массива:

Рис. 10.3. Результаты быстрой сортировки массива

Вариант 1

25. Какие программы корректны по отношению к своим спецификациям?

q {n=5}int fact(int n){int f=0; for (int i=0; i< n; i++) f*=i; return(f);}{result = n!};

q {n=5}int fact(int n){return(120);}{result = n!};

q {false}int fact(int n){int f=0; for (int i=0; i< n; i++) f*=i; return(f);}{result = n!};

q {n целое & n>0}int fact(int n){int f=1; for (int i=1; i< n; i++) f*=i; return(f);}{result = n!};.

26. Отметьте истинные высказывания:

q завершающийся, частично корректный метод тотально корректен;

q в рекурсивной процедуре должна присутствовать нерекурсивная ветвь;

q многопроцессорный современный компьютер решит задачу «Ханойские башни» в течение суток;

q квадратичные методы сортировки, требующие O(n²) операций всегда работают медленнее, чем сортировки с порядком операций O(n*log(n)).

q Каждый цикл имеет только один инвариант.

27. Вариантом цикла является:

q любое логическое выражение;

q любое арифметическое выражение;

q любое целочисленное арифметическое выражение;

q целочисленная переменная.

Вариант 2

28. Для программы, вычисляющей сумму первых n элементов массива:
S=A[0]; k=0; while(k!=(n-1)) { k++; S+=A[k];}
инвариантом цикла являются:

q S = ;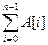

q S = ;

q S = ;

q k > 0;

q S= A[k].

29. Отметьте истинные высказывания:

q незавершающийся метод тотально корректен;

q рекурсивным называется метод, в теле которого содержится вызов другого метода;

q цикл имеет сколь угодно много инвариантов.

q нерекурсивный алгоритм может найти решение задачи «Ханойские башни» за меньшее число ходов.

30. Постусловие метода:

q может иметь значение true;

q может иметь значение false;

q представляет логическое выражение, связывающее входные и выходные аргументы, которое должно быть истинным после завершения метода;

q невыполнение постусловия после завершения метода всегда говорит об ошибке в работе метода;

q метод корректен, если предусловие истинно на входе, а постусловие на выходе.

Вариант 3

31. Для программы, вычисляющей сумму первых n элементов массива:
S=A[0]; k=0; while(k!=(n-1)) { k++; S+=A[k];}
подходящими инвариантами цикла являются:

Дата добавления: 2014-12-25