Перетворення Фур’є. Частотні характеристики

Перетворення Фур’є є окремим випадком перетворення Лапласа за умови: s=0, тобто s = jw.

Тоді відповідно до (5.6) перетворення Фур’є має вигляд:

(5.27)

або в символічній формі:

x(t) ® X(jw); X(jw) = F{x(t)}, (5.28)

де F - оператор Фур’є.

Усі теореми та властивості перетворення Лапласа справедливі й для перетворення Фур’є (у частотній зоні). Потрібно лише змінну s замінити на .

Оскільки W(s)=Y(s)/X(s), то з урахуванням сказаного вище можна записати:

W(jw) = Y(jw)/X(jw). (5.29)

Цю передавальну функцію називають частотною або комплексною (КПФ). Частотна передавальна функція - це відношення Фур’є-зображення вихідної величини до Фур’є-зображення вхідної величини за нульових початкових умов.

Частотна передавальна функція W(jw) є комплексною функцією від змінної w. Її, як і будь-яке комплексне число, можна записати в алгебраїчній та показниковій формі:

W(jw) = U(w) + jV(w) = A(w)×e^jj(w) , (5.30)

де U(w) = Re{W(jw)} - дійсна частина КПФ, яка називається дійсною частотною функцією; графік цієї функції називається дійсною частотною характеристикою (ДЧХ);

V(w) = Im{W(jw)} - уявна частина КПФ, яка називається уявною частотною функцією, а її графік - уявною частотною характеристикою (УЧХ);

A(w) = |W(jw)| - модуль КПФ - амплітудна частотна функція, причому

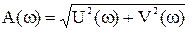. (5.31)

Графік цієї функції називають амплітудною частотною характеристикою (АЧХ);

j(w) = Arg{W(jw)} - аргумент КПФ, який називають фазовою частотною функцією:

j(w) = arctg V(w)/U(w). (5.32)

Графік цієї функції називається фазовою частотною характеристикою (ФЧХ).

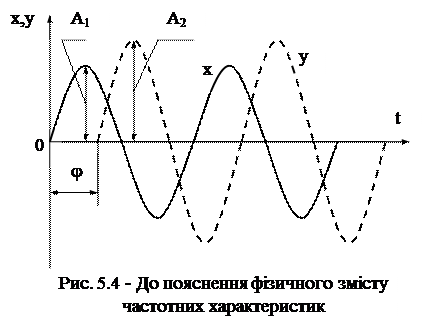
Пояснимо фізичний зміст АЧХ і ФЧХ. Якщо на вхід системи подати гармонічний сигнал частоти w: x(t) = A₁sin(wt + j₁), то на виході в усталеному режимі отримаємо гармонічний сигнал тієї самої частоти w: y(t)= A₂sin(wt + j₂), амплітуда і початкова фаза якого може відрізнятися від амплітуди та початкової фази вхідного сигналу (рис. 5.4).

АЧХ - це залежність зміни відношення амплітуди вихідного сигналу A₂ до амплітуди вхідного сигналу A₁ від частоти w вхідного сигналу, тобто

(5.33)

ФЧХ - це залежність зсуву по фазі між вхідним і вихідним сигналами від частоти w вхідного сигналу, тобто

j(w)=j₂(w)-j₁. (5.34)

Саму частотну передавальну функцію W(jw) називають також амплітудно-фазовою частотною функцією, а її графік на комплексній площині - амплітудно-фазовою частотною характеристикою (АФЧХ або АФХ).

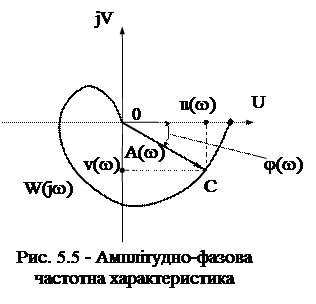На комплексній площині (рис.2.5) W(jw) визначає вектор 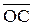, довжина якого дорівнює A(w), а аргумент (кут між вектором і дійсною додатною піввіссю) - j(w).

Крива, яку описує кінець вектора функції W(jw) при зміні частоти w від 0 до ¥, називається АФЧХ.

Окрім перелічених частотних характеристик (АФЧХ, АЧХ, ФЧХ, ДЧХ, УЧХ), під час аналізу та синтезу САК широко застосовуються також логарифмічні частотні характеристики (ЛЧХ):

ЛАЧХ - логарифмічна амплітудна частотна характеристика;

ЛФЧХ - логарифмічна фазова частотна характеристика;

ЛЧХ - це ті самі частотні характеристики системи, але побудовані в іншій системі координат:

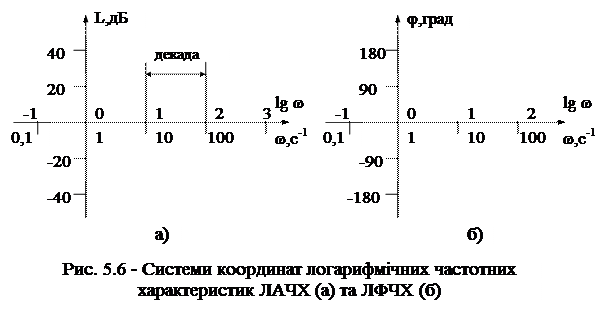
- по вісі абсцис відкладають частоту в логарифмічному масштабі: на поділці, що відповідає значенню lg(w), пишуть значення w; одиницею виміру слугує декада - інтервал, на якому частота змінюється в десять разів;

- по вісі ординат значення A(w) відкладають у децибелах (дБ), а значення j(w)- у градусах або радіанах.

Логарифмічною амплітудною частотною характеристикою системи називають АЧХ цієї системи, виражену в децибелах і побудовану в логарифмічному масштабі частот.

ЛАЧХ та АЧХ зв’язані співвідношенням:

L(w)= 20 lg A(w) = 20 lg |W(jw)|. (5.35)

Логарифмічною фазовою частотною характеристикою САК називають залежність фази j, виражену в градусах чи радіанах, від частоти w в логарифмічному масштабі.

ЛЧХ мають переваги перед звичайними АЧХ та ФЧХ: вони більш наочні та прості в побудові. Системи координат ЛАЧХ та ЛФЧХ показані на рис. 5.6.

Приклад. Для умови попереднього прикладу записати комплексну передавальну функцію W(jw). Визначити і побудувати частотні характеристики: амплітудно-частотну (АЧХ); фазову частотну (ФЧХ); амплітудно-фазову частотну (АФЧХ); логарифмічну амплітудно-частотну (ЛАЧХ).

Змінюємо в функції 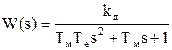змінну s на jw і отримуємо комплексну передавальну функцію:

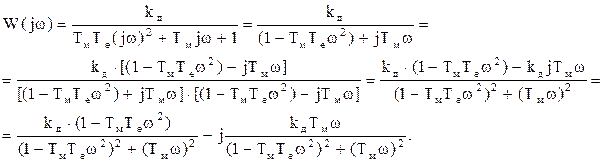
Тобто, дійсна частотна функція , уявна частотна функція .

Амплітудна частотна функція:

.

Фазова частотна функція: 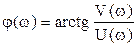. З урахуванням знаків дійсної та уявної функцій: 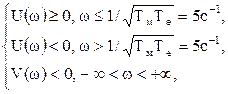маємо:

Логарифмічна амплітудна частотна функція:

.

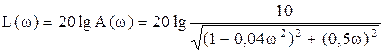Відповідні характеристики наведені на рис. 5.7.

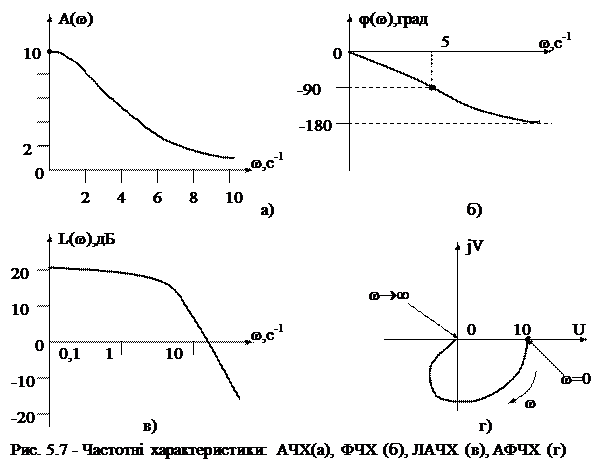Отже, після вивчення попереднього матеріалу можна зробити такий висновок.

Класичний метод дослідження лінійних САК ґрунтується на складанні та подальшому розв’язку диференціальних рівнянь, що зв’язують вихідну координату y(t) з вхідним впливом x(t). Диференціальні рівняння - це перша форма математичної моделі САК. Через складність реальних систем і впливів складання та розв’язок цих рівнянь є складною задачею, яка потребує застосування ЕОМ.

Мета дослідження спрощується при введенні другої форми математичної моделі - передавальної функції за Лапласом, оскільки перетворення Лапласа дозволяє замінити диференціальні рівняння на алгебраїчні.

Третя форма математичної моделі - частотні характеристики - дозволяють розв’язувати алгебраїчні рівняння графічно, що також спрощує задачу. Крім того, частотні характеристики дають ясне фізичне тлумачення властивостей системи.

5.5. Типові динамічні ланки та їх характеристики

Дата добавления: 2014-12-25