Решение тренировочных заданий. Проведем сначала отделение корней данного уравнения

Задание I.

Проведем сначала отделение корней данного уравнения. Это уравнение алгебраическое уравнение третьей степени. Найдем границы его корней.

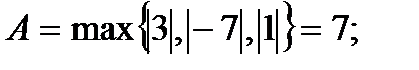
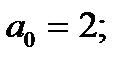
Таким образом, все корни уравнения находятся внутри отрезка 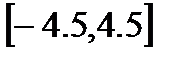. Определим знаки функции в различных точках этого отрезка.

X	-4,5	-4	-3	-2	-1
f(x)	-	-	-	+	+	+	-	+

На концах отрезков [-3; -2], [0; 1], [1; 2] непрерывная функция f(x) имеет разные по знаку значения, следовательно, в каждом из этих отрезков содержится по крайней мере один корень уравнения. Поскольку алгебраическое уравнение третьей степени может иметь не более трех действительных корней, то в каждом из этих отрезков содержится ровно один корень уравнения. Таким образом, задача отделения корней данного уравнения решена:

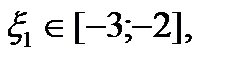
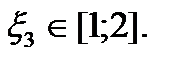
33Решение. В задаче 2 показано, что наибольший корень данного уравнения принадлежит отрезку [1; 2]. Следовательно, уточнение корня необходимо производить до тех пор, пока не будет достигнута точность ε=0,05. Производная f ^/(x) = 6x² + 6x – 7 на рассматриваемом отрезке [1;2] положительна, причем

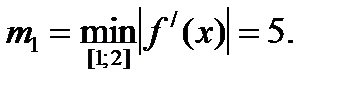
Вторая производная f ^//(x) = 12x + 6 тоже положительна на отрезке [1; 2]. Вычислим f(1) = -1; f(2) = 15. Очевидно, что начальное приближение х₀ = 1, а с = 2. Перейдем непосредственно к уточнению корня по формуле (4):

.

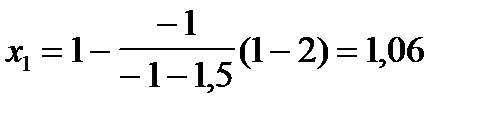Оценим погрешность полученного приближенного значения по формуле (5), предварительно определив f(x₁)= -0,67.

Δx₁ = 0,67 / 5 = 0,14.

Поскольку требуемая точность еще не достигнута (Δх₁ > ε), продолжим вычисления, а весь процесс решения оформим в виде следующей таблицы:

Таблица 2.

n	Xn	f(xn)	Δxn
	1,06 1,10 1,12 1,14	-0,68 -0,41 -0,27 -0,12	0,14 0,09 0,06 0,03

Из таблицы 2 видно, что погрешность метода Δх₄ = 0,03 меньше требуемой точности ε =0,05.

Далее, поскольку все вычисления проводились с двумя знаками после запятой, то необходимо учесть погрешность округления, равную 0,005. Окончательный результат следует представить в виде:

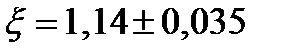
Задание II.

Вычислим значение функции на концах отрезка [0; 1] f(0)=1; f(1)= -1. Определив первую и вторую производные, заметим, что первая производная меняет свой знак на отрезке [0; 1]. Сузим рассматриваемый отрезок так, чтобы на новом отрезке первая производная не меняла знака. Рассмотрим середину отрезка [0; 1] - точку 0,5. Вычислим значение функции в этой точке: f(0,5)= -1,5. Следовательно, корень данного уравнения принадлежит отрезку [0; 0,5]. На этом новом отрезке первая производная сохраняет свой знак (отрицательна), вторая производная тоже сохраняет знак (положительна). Вычислим

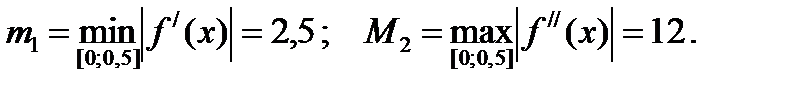
Так как на левом конце отрезка [0; 0,5] функция f(x) имеет тот же знак, что и ее вторая производная, в качестве начального приближения возьмем точку 0: х₀ = 0.

х₁ = 0 – 1 / (-7) = 0,143.

Погрешность этого значения есть (формула (7)):

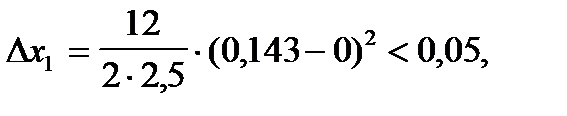
что больше требуемой точности ε = 0,005, поэтому следует перейти к вычислению приближения х₂.

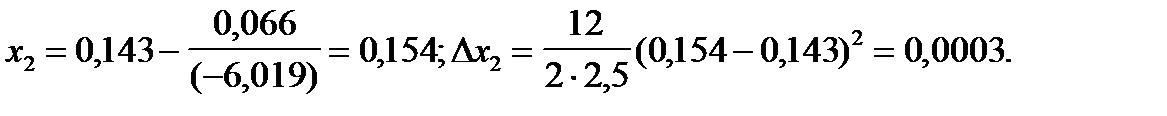
Погрешность второго приближения Δх₂ = 0,0003 меньше требуемой точности ε = 0,005. Учитывая погрешность округления, равную 0,0005, получим:

Задание III.

Отрицательный корень данного уравнения находится на отрезке [-3; -2].

Вычислим:

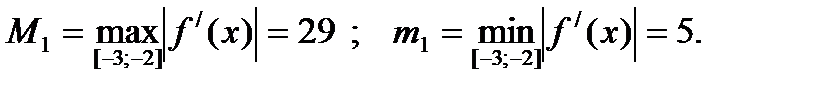
Таким образом, итерационный процесс (11) примет следующий вид:

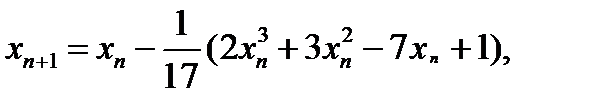n = 0, 1, 2, …,

а оценка погрешности (12)

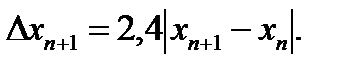
В качестве начального приближения примем середину рассматриваемого отрезка [-3; -2]: x₀ = -2,5.

Далее вычислим приближение корня:

x₁ = x₀ – 1 / 17(2x₀³ +3x₀² –7x₀ + 1) = -2,853.

Оценим погрешность приближенного значения x₁ :

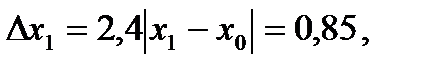
что больше требуемой точности ε = 0,05, поэтому следует перейти к вычислению х₂ и его погрешности.

Дальнейшие рассуждения аналогичны вышеприведенным, а весь итерационный процесс удобно оформить в виде следующей таблицы:

Таблица 3.

N	Xn-1	Xn	Δ Хn
1. 2. 3. 4.	-2,5 -2,857 -2,791 -2,816	-2,853 -2,791 -2,816 -2,807	0,848 0,149 0,060 0,022

Из таблицы 3 видно, что требуемая точность достигнута и можно принять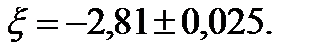

Следует отметить, что все вычисления велись с двумя запасными знаками, а погрешность округления (0,003) добавлена к погрешности метода.

Дата добавления: 2014-12-25