Решение тренировочных заданий

Задание I.

Приведем систему к виду, в котором элементы главной диагонали превосходили бы сумму модулей остальных элементов строки. Это обеспечит выполнение условия (9): ||c||m < 1.

7,6x1+0,5x2+2,4x3=1,9;	(I + II)
2,2x1+9,1x2+4,4x3=9,7;	(2III + II – I)
–1,3x1+0,2x2+5,8x3=–1,4.	(III – II)

Отсюда

10x1=2,4x1–0,5x2–2,4x3+1,9;

10x2=–2,2x1+0,9x2–4,4x3+9,7;

10x3=1,3x1–0,2x2+4,2x3–1,4.

В окончательном виде наша система запишется следующим образом:

x1=0,24x1–0,05x2–0,24x3+0,19;

x2=–0,22x1+0,09x2–0,44x3+0,97;

x3=0,13x1–0,02x2+0,42x3–0,14.

Матрица c и вектор 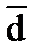для этой системы будут иметь вид:

;

.

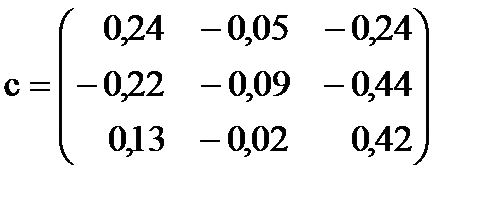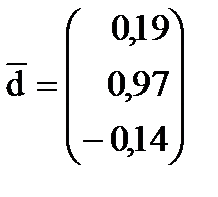Нормы матрицы c, вектора 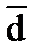будут соответственно равны:

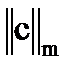= max(0,24+0,05+0,24; 0,22+0,09+0,44; 0,13+0,02+0,42)=

= max(0,53; 0,75; 0,67)=0,75<1.

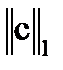= max(0,24+0,22+0,13; 0,05+0,09+0,02; 0,24+0,44+0,42)=

= max(0,59; 0,16; 1,10)=1,10>1.

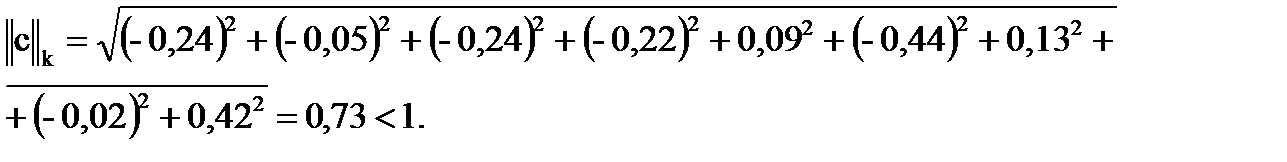
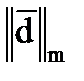=max(0,19; 0,97; 0,14)=0,97.

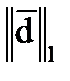=max(0,19+0,97+0,14)=1,30.

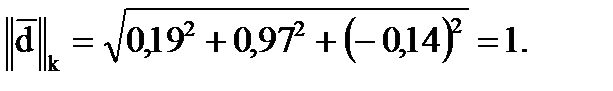
Т.к. 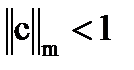, то процесс итераций сходится, и теоретическое число итераций k будет определяться по формуле:

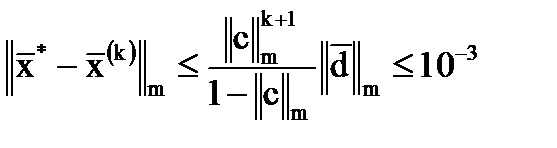, или

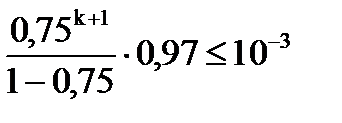, т.е.

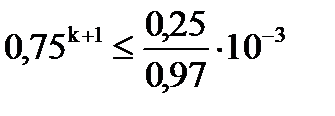
Отсюда k³28.

Теоретическая оценка числа итераций, необходимых для обеспечения заданной точности, практически всегда очень завышена.

Вычисления располагаем в таблице.

Номер итерации	x1	x2	x3
	0,19	0,97	–0,14
	0,2207	1,0703	–0,1915
	0,2354	1,0988	–0,2118
	0,2424	1,1088	–0,2196
	0,2454	1,1124	–0,2226
	0,2467	1,1138	–0,2237
	0,2472	1,1143	–0,2241
	0,2474	1,1145	–0,2243

На 7 итерации имеем, что

.

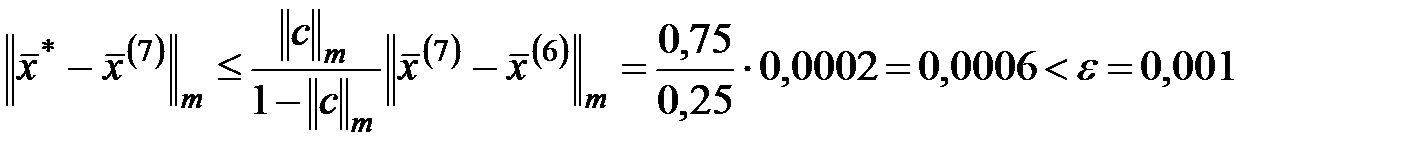Следовательно, необходимая точность достигнута.

Ответ: x1=0,2474; x2=1,1145; x3=–0,2243.

Глава 4. ИНТЕРПОЛИРОВАНИЕ.

Задача приближения (аппроксимации) функций возникает и как самостоятельная, и при решении многих других задач. Простейшая ситуация, приводящая к приближению функций, заключается в следующем. При некоторых значениях аргумента х₀, х₁,…х_n, называемых узлами, заданы значения функции y_i=f(x_i), i=0,1...,n. Требуется восстановить значения функции при других x. Подобная же задача возникает при многократном вычислении на ЭВМ одной и той же сложной функции в различных точках. Вместо этого часто бывает целесообразно вычислять значения этой функции в небольшом числе характерных точек x_i, а в остальных точках вычислять ее значения по некоторому более простому правилу, используя информацию об уже известных значениях y_i.

Другими распространенными примерами приближения функций являются задачи определения производной f'(x) и интеграла 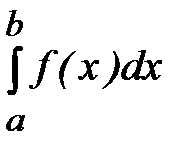по заданным значениям y_i.

Классический подход к решению подобных задач заключается в том, чтобы, используя имеющуюся информацию о функции f(x), рассмотреть другую функцию 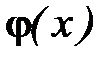, близкую к f(x), позволяющую выполнить над ней соответствующую операцию и получить оценку погрешности такой «аналитической замены».

При выборе класса, к которому принадлежит аппроксимирующая функция 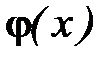, следует руководствоваться тем, что 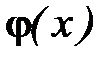, с одной стороны, должна отражать характерные особенности аппроксимируемой функции f(x), с другой стороны, быть достаточно удобной в обращении.

Вопрос о близости аппроксимируемой и аппроксимирующей функций решается по-разному. Если параметры, от которых зависит функция 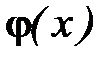, определяются из условия совпадения значений функций f(x) и 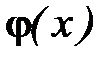в узлах, то такой способ аппроксимации называется интерполированием (интерполяцией).

Наличие большого количества различных способов приближения объясняется многообразием различных постановок задачи. Далее мы рассмотрим лишь один раздел теории приближения – интерполирование многочленами. Аппарат интерполирования многочленами является важнейшим аппаратом численного анализа. На его основе строится большинство численных методов решения других задач.

Дата добавления: 2014-12-25