Разностные методы решения дифференциальных уравнений

Метод Рунге-Кутта решения уравнения второго порядка.

Очевидно, что уравнение второго порядка, следовательно, к ним также будет применим метод Рунге-Кутта.

Рассмотрим уравнение второго порядка

Y’’=f(x,y,y’) (100)

И будем отыскивать его решение, удовлетворяющее начальным условиям:

Y(x₀)=y₀, y’(x₀)=y’_0. (101)

Это уравнение может быть сведено к системе

Y’=z

Z’=f(x,y,z) (102)

С начальным условием

Y(x₀)=y₀, z(x₀)=z₀ (103)

В частности, расчетные формулы Эйлера (r=I) будут иметь вид

Y_k+1=y_k +Δy_k, Δy _k=hz_k, (104)

z_k+1=z_k +Δz_k Δz_k=hf(x_k,y_k,z_k), (k=0,1,…).

Расчетные формулы метода Рунге-Кутта, имеющие погрешность на одном шаге h⁵ (r=4), определяются выражениями (97)-(98), причем вычисления по ним упрощаются за счет более простого вида правых частей системы (102).

Пример 8. Методом Рунге-Кутта (97)-(98) найти решение дифференциального уравнения

Y’’=y, (105)

Удовлетворяющее начальным условиям:

Y(0)=1, y’(0)=1 (106)

На отрезке [0,0;0,2], взять шаг h=0,1.

Решение. Заменим уравнение (105) системой уравнений

Y’=z=f(x,y,z), z’=y=g(x,y,z) (107)

Причем y(0)=I, z(0)=I.

Вычисления проведем с точностью до шестого знака после запятой. Значения точного решения задачи (105)-(106) – функции е^x – приведены в пятом столбце в таблице 10. Очевидно, в нашем случае имеют место равенства:

Y=z; k_I=l_I, Δy=Δz,

Поэтому таблица 10 будет иметь следующий вид:

Таблица 10.

x	Y=z	LI=kI=hy	Δy=Δz	e^x
0,0	1,000000	0,100000	0,100000
0,05	1,050000	0,105000	0,210000
0,05	1,052500	0,105250	0,210500
0,1	1,105250	0,110525	0,110525
0,1	1,105171		1,105171	1,10517
0,1	1,105171	0,110517	0,110517
0,15	1,160430	0,116043	0,232086
0,15	1,163192	0,116319	0,232638
0,2	1,221490	0,122149	0,122149
0,2	1,221403		0,116232	1,22140

Сравнение с точным решением (e^x) показывает, что в полученных значениях после запятой – пять верных знаков.

Недостатком рассмотренного выше метода Рунге-Кутта является то, что получение одного значения решения дифференциального требует подсчета правой части уравнения – функции f(x,y) в нескольких точках. Если функция f(x,y) сложна, то объем вычислительной работы велик.

В разностных методах решения обыкновенных дифференциальных уравнений требуется только однократное вычисление правой части на каждом шаге. Ограничимся случаем одного уравненияпервого порядка.

3.1. Экстраполяционная формула Аламса

Пусть требуется найти решение уравнения

(108)

Удовлетворяющее начальному условию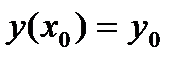

На отрезке [ ].

Разобьем отрезок на n – равных частей

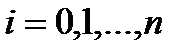, (109)

Предположим, что уже найдены каким-то образом приближенные значения y(x) в точках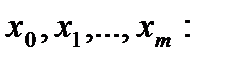

(110)

и следовательно, известны значения функции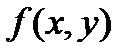

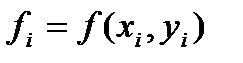, i=0,1,…,m (111)

Для того, чтобы определить значение функции в точке 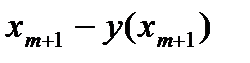, проинтегрируем уравнение (108) в пределах 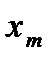по

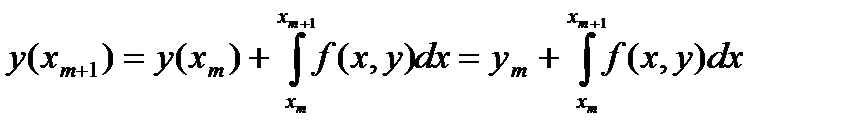(112)

По известным значениям функции 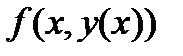(111)

Можно построить то или иное приближенное представление функции 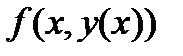, например, в виде интерполяпионного полинома , который можно подставить в правую часть выражения (112) и проинтегрироывать.

Тогда можно приближенно считать:

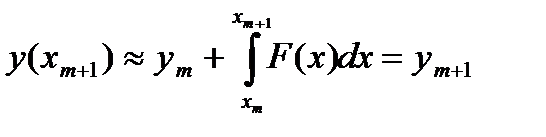(113)

Таким образом, таблица значений функции y(x) продвинется еще на один шаг и т.д. Для построения функции F(x) воспользуемся второй интерполяционной формой Ньютона, так как точка находится в конце таблицы .

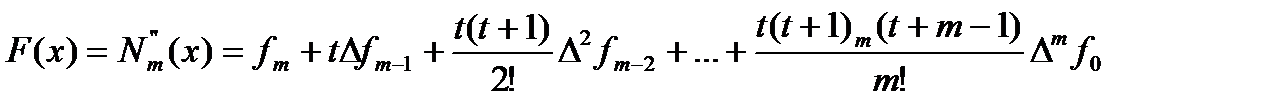; (114)

Где .

Подставляя (114) в (113) получим (115)

Сделаем в (115) замену переменной

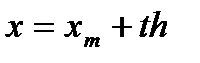(116)

И получим

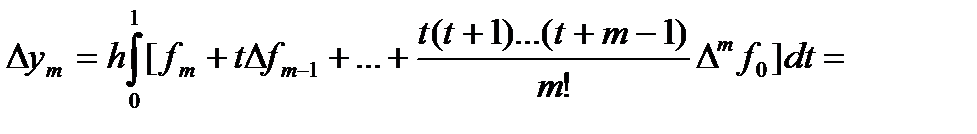
(117)

где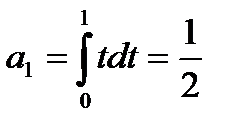

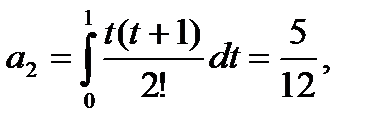
(118)

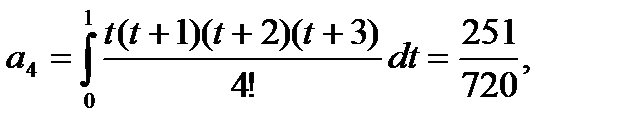
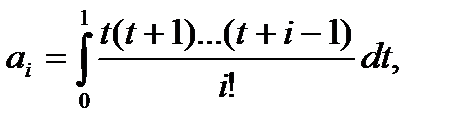i=1,2,...,m.

Таким образом формула (117) примет вил

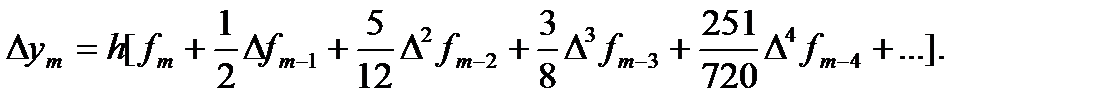(119)

Если обозначить

(120)

То формулу (119) можно переписать в виде

(121)

Полученная формула носит название экстраполяционной формулы Адамса. Формула называется экстрвляционной в связи с тем, что она получена путем интегрирования интерполяционнго многочлена, построенного по узлам: 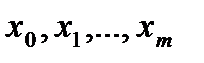, а используется для вычисления значения функции в точке 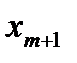, лежащей вне отрезка .

Отбрасывая в (121) члены, начиная с некоторого, будем получать экстраполяционные формулы Адамса, имеющие различный порядок погрешности на одном шаге. Например, если в (121) ограничиться первыми четырьмя членами (в предположении, что третьи разности практически постоянны), получаем формулу

(122)

Для которой по известным значениям

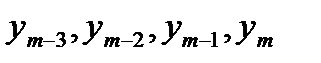находим

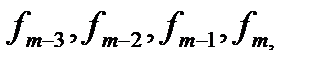затем

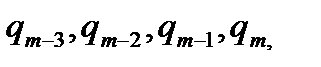и соответствующие разности

Определив по формуле (122)

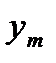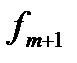, прибавим его к и найдем Затем вычислим и 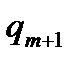и продвинемся в таблице значений и ее разностей на 1шаг, вычислим по формуле и 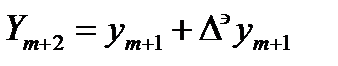и т.д.

Таблица вычислений и по экстраполяционной формуле Адамса имеет вид:

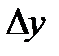
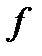
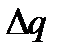
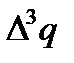
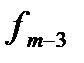
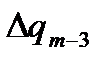
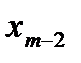
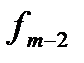
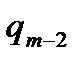
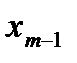
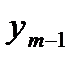
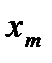
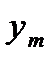
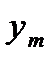
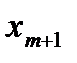
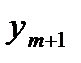
Очевидно, что для начала процесса вычисления по формуле Адамса (122) нужно четыре начальных значения по которым можно вычислить и :

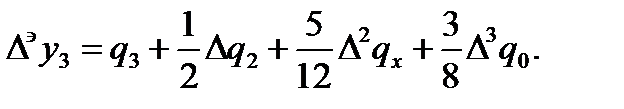(123)

Начальный отрезок, значения находят исходя из начального условия одним из известных методов. Обычно начальный отрезок находят методолм Рунге-Кутта. Метод Адамса, таким образом заключается в продолжении таблицы разностей с помощью формулы (122).

Замечание. Если в таблице разностей практически постоянными являются разности второго порядка, то формула Адамса (121) будет содержать только 3 члена, а начальный участок – 3 точки . Если практически постоянными являются только четвертые разности, то начальный участок содержит 5 точек и т.д. Вообще, в случае использования формулы Адамса (121) до m-разностей, начальный участок будет содержать точку.

Дата добавления: 2014-12-25