
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Розкриття невизначеностей різних видів
|
|
|
|
Теорема 7.1.5 (Правило Лопіталя розкриття невизначеностей вигляду). Нехай функції і неперервні і диференційовані в точці хо (окрім, може, бути, точки хо), і в цьому околі,. Якщо існує границя то.
Теорема 7.1.4. (правило Лопіталя розкриття невизначеностей вигляду). Нехай функція і неперервна і диференційована в околі і обертаються в нуль в цій точці:. Нехай в околі точки. Якщо існує границя, то.
Правила Лопіталя
Правило Лопіталя. Розкриття невизначеностей різних типів.
Розглянемо спосіб розкриття невизначеностей вигляду і, який заснований на застосуванні похідних.
□ Застосуємо до функцій 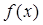 і
і 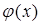 теорему Коші для відрізка
теорему Коші для відрізка  , що лежить в околі точки хо. Тоді
, що лежить в околі точки хо. Тоді  , де с лежить між хо і х (Рис.144). Враховуючи, що
, де с лежить між хо і х (Рис.144). Враховуючи, що 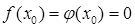 , одержуємо
, одержуємо


При, величина з також прагне до; перейдемо в рівності (25.4) до границі:
 .
.
Рис. 144.
Оскільки 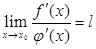 , то. Тому
, то. Тому 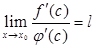 .
.
Коротко отриману формулу читають так: межа відношення двох нескінченно малих рівна границі відношення їх похідних, якщо останній існує.■
Зауваження: 1. Теорема 7.1.4 вірна і у разі, коли функції і не визначені при, але і. Достатньо, поклавши, отримаємо
 .
.
3. Якщо похідні  і
і  , теорему 7.1.4 можна застосувати ще раз:
, теорему 7.1.4 можна застосувати ще раз:

і т.д.
Приклад 7.1.2. Знайти  .
.
○ 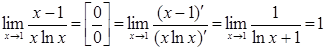 .●
.●
Приклад 7.1.3. Знайти 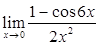 .
.
○ 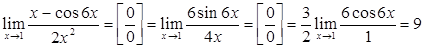 .●
.●
Теорема 7.1.4 дає можливість розкривати невизначеність вигляду  . Сформулюємо без доказу теорему про розкриття невизначеність вигляду.
. Сформулюємо без доказу теорему про розкриття невизначеність вигляду.
Приклад 7.1.4. Знайти 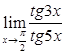 .
.
○ 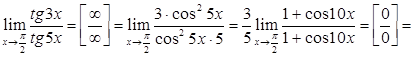

2-й спосіб:
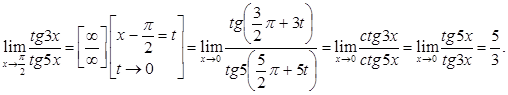 ●
●
Правило Лопіталя застосовується для розкриття невизначеностей вигляду  ,
, 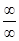 які називають основними. Невизначеності вигляду,
які називають основними. Невизначеності вигляду, 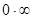 зводяться до двох основних видів шляхом тотожних перетворень.
зводяться до двох основних видів шляхом тотожних перетворень.
1. Нехай при. Тоді очевидні наступні перетворення:
|
|
|
 (або).
(або).
Наприклад:

2. Нехай при. Тоді можна поступити так:
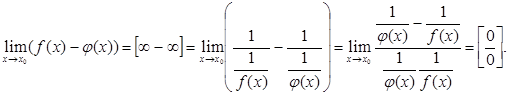
На практиці простіше, наприклад

3. Нехай або  і або
і або 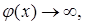 , і
, і  або
або 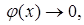 , і при
, і при 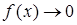 Для знаходження границі вигляду
Для знаходження границі вигляду 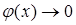 зручно спочатку прологарифмувати вираз
зручно спочатку прологарифмувати вираз 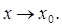
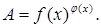
Приклад 7.1.5 Знайти 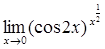
○ Маємо невизначеність вигляду. Логарифмуємо вираз, отримаємо: Потім знаходимо межу:
 , тобто Звідси, і.
, тобто Звідси, і.
Розв’язання можна оформити коротше, якщо скористатися «готовою формулою»

(використана основна логарифмічна тотожність: 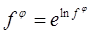 ).●
).●
Приклад 7.1.4. Знайти 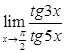 .
.
○ 
 ●
●
Приклад 7.1.7 Нехай

Знайти  (Додатково: знайти
(Додатково: знайти  )
)
○ При маємо
 .
.
При за визначенням похідної:
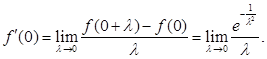
Робимо заміну і застосовуємо правило Лопіталя

Таким чином

Аналогічно можна показати, що 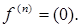 ●
●
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 2147; Нарушение авторских прав?; Мы поможем в написании вашей работы!