
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Застосування визначеного інтеграла. Площа криволінійної трапецію
|
|
|
|
Інтегрування по частинам у визначеному інтегралі.
Теорема 9.5.2. Якщо функції 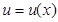 і
і 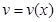 мають неперервні похідні на відрізку
мають неперервні похідні на відрізку  , то має місце формула
, то має місце формула
 . (9.5.2)
. (9.5.2)
□ На відрізку  має місце рівність
має місце рівність  . Отже, функція
. Отже, функція  є первісною для неперервної функції
є первісною для неперервної функції 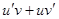 . Тоді по формулі Ньютона-Лейбніца маємо:
. Тоді по формулі Ньютона-Лейбніца маємо:
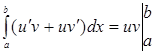 .
.
Отже,
 .■
.■
Формула (39.2) називається формулою інтегрування по частинах для визначеного інтеграла.
Приклад 9.5.2. Обчислити 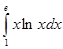 .
.
○ Покладемо  .
.
Використовуючи формулу (9.5.2), отримаємо
 .
.
Приклад 9.5.3. Обчислити інтеграл  .
.
○ Розв’язання: Інтегруємо по частинах. Покладемо
 .
.
Тому
 .
.
Формулу трапецій отримують аналогічно формулі прямокутників: на кожному частковому відрізку криволінійна трапеція замінюється звичайною.
Розіб'ємо відрізок  на
на 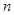 рівних частин довжини
рівних частин довжини 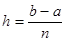 . Абсциси точок поділу
. Абсциси точок поділу 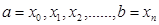 (рис..201). Нехай
(рис..201). Нехай  відповідні їм ординати графіка функції. Тоді розрахункові формули для цих значень матимуть вигляд
відповідні їм ординати графіка функції. Тоді розрахункові формули для цих значень матимуть вигляд 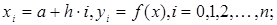
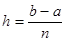 .
.
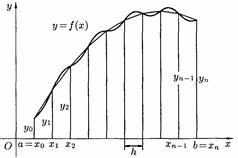
(рис.201)
Замінимо криву 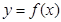 ламаною лінією, ланки якої сполучають кінці ординат
ламаною лінією, ланки якої сполучають кінці ординат 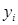 і
і 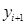
 . Тоді площа криволінійної трапеції приблизно дорівнює сумі площ звичайних трапецій з підставами
. Тоді площа криволінійної трапеції приблизно дорівнює сумі площ звичайних трапецій з підставами  і висотою
і висотою 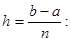

або
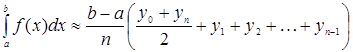 . (9.8.2)
. (9.8.2)
Формула (9.8.2) називається формулою трапецій.
Абсолютна похибка 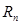 наближення, отриманого по формулі трапецій, оцінюється за допомогою формули
наближення, отриманого по формулі трапецій, оцінюється за допомогою формули  , де
, де 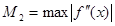 . Знову для лінійної функції
. Знову для лінійної функції 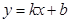 формула (9.8.2) – точна.
формула (9.8.2) – точна.
????????(68-72)
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 846; Нарушение авторских прав?; Мы поможем в написании вашей работы!