Коэффициент корреляции

В рассмотренном примере корреляционной связи оба коэффициента регресси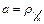и и 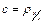положительны. В таком случае корреляцию называют положительной, что имеет место при изменении изучаемых количественных признаков в одинаковом направлении (х и у одновременно возрастают или одновременно убывают).

Прямые при положительных коэффициентах регрессии образуют острые углы с соответствующими осями координат (рис. 14) — у прямой регрессии у по х коэффициент регрессии , где a — острый угол, образованный прямой I с осью Ох, а у прямой регрессии х по y коэффициент регрессии , где b — острый угол, образованный прямой II с осью Оу. При отрицательных коэффициентах регрессии прямые регрессии образуют с соответствующими осями тупые углы.

Для большей наглядности на рис. 14 показано положение прямых регрессии относительно новой системы координат с началом в точке пересечения этих прямых.

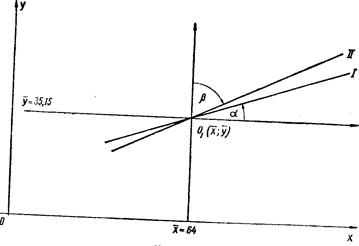
Рис. 14

Сами по себе значения коэффициентов регрессии не позволяют судить о тесноте связи между х и у. Это зависит от величины угла, образованного прямыми регрессии. Чем меньше этот угол, тел; теснее корреляционная связь между х и у.

При слиянии этих двух прямых в одну имеет место линейная функциональная зависимость между х и у.

В качестве меры тесноты линейной корреляционной связи принимается коэффициент корреляции

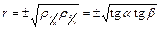
со знаком, совпадающим со знаками коэффициентов регрессии. При этом, если прямые I и II совпадают, то и 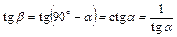. Но тогда 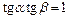и, следовательно, .

Обращение коэффициента корреляции в 1 или в -1 является, как это можно доказать, необходимым и достаточным признаком. линейной функциональной зависимости между х и у.

Корреляционная таблица в таких случаях состоит из расположенных лишь на одной диагонали частот значений х и у.

Вместе с тем, когда, по крайней мере, один из углов a или b равен нулю, то и 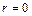, а значит, и между рассматриваемыми величинами не существует ни функциональной, ни корреляционной линейной зависимости. Однако в этом случае между х и у возможны нелинейные корреляционные и даже функциональные связи.

Корреляционная зависимость между х и у (для положительных коэффициентов регрессии) имеет место, когда коэффициент корреляции, как это можно доказать, выражается правильной дробью (0 < r < 1). При этом связь между переменными тем теснее, чем ближе коэффициент корреляции к 1.

Введенное определение коэффициента корреляции в виде позволяет на основании выражений коэффициентов регрессии получить удобную формулу для непосредственного вычисления коэффициента корреляции.

Если обратиться к выражениям коэффициентов прямых регрессии

и ,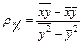

то можно заметить, что знаменатели в обоих выражениях обозначают дисперсии соответствующих рядов распределений:

и .

Отсюда можно получить для коэффициента корреляции формулу

,

которая сразу показывает, что между независимыми величинами корреляции не существует, так как для таких величин выполняется равенство .

Замечание. Последнее равенство является приближенным, а поэтому если коэффициент корреляции очень мал , считают, что линейной корреляции между х и у нет.

Записанная выше формула позволяет выразить каждый коэффициент регрессии через коэффициент корреляции.

Так, коэффициент регрессии у по x

,

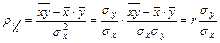а коэффициент регрессии х по у

.

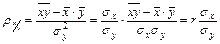Такие выражения коэффициентов регрессии показывают, что составление уравнений прямых регрессии может быть облегчено, если будет найдено значение коэффициента корреляции. Для его вычисления следует использовать выражения числителя и знаменателя:

.

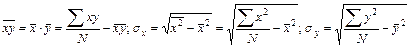Тогда можно вычислить коэффициент корреляции по формуле

.

Пример 1. В табл. 6 дана группировка 135 сахаропесочных заводов по размеру производственных основных средств в млн. руб. (х) и по среднесуточной переработке свеклы в тыс. ц (у). Требуется определить коэффициент корреляции и составить уравнения регрессии.

Таблица 6

y x
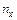
1,75 2,25 2,75 3,25 3,75 4,25	¾ ¾ ¾	¾ ¾	¾		¾	¾	¾ ¾	¾ ¾ ¾ ¾ ¾	¾ ¾ ¾ ¾ ¾	21 42 25 24 13 10

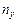
Расположение рядов распределения значений у в табл. 6 позволяет наметить линейную корреляционную связь между х и у.

Для отыскания коэффициента корреляции составим вспомогательную таблицу.

Таблица 7

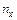
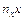
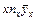
	21×1,75 42×2,25 25×2,75 24×3,25 13×3,75 10×4,25	21×3,0625 42×5,0625 25×7,5625 24×10,5625 13×14,0625 10×18,0625	1,75×114 2,25×250 2,75×171 3,25×161 3,75×102 4,25×93		12×4 22×5 35×6 31×7 21×8 6×9 5×10 2×11 1×12	12×16 22×25 35×36 31×49 21×64 6×81 5×100 2×121 1×144	4×28,00 4×51,50 6×83,75 7×87,75 8×65,75 9×21,00 10×18,75 11×8,50 12×4,25
N =135	369,25	1082,9375	2533,25				2533,25

Следует пояснить, что вторые множители в четвертом столбце 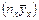получены из данных табл. 6 суммированием произведений каждого числа внутренней строки на соответствующее значение у (например, 114=4×4+6×5+9×6+2×7; 171= 4×5+6×6+7×7+8×7+1×10).

Так как суммирование этих вторых множителей дает сумму всех значений у, то сумма , и это равенство подтверждает правильность подсчета суммы всех значений у. Аналогична структура вторых множителей в последнем столбце. Например, 28 = 4×1,75+5×2,25+3×3,25. Здесь суммирование вторых множителей дает сумму всех значений х, а потому равенство служит для подтверждения правильности подсчета. Вместе с тем итоговые суммы по четвертому и последнему столбцам являются в то же время суммами всех участвующих в таблице парных произведений ху. Отсюда .

По данным подсчетов имеем:

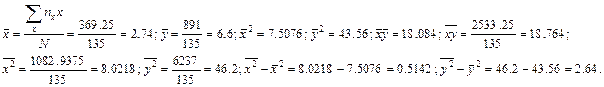
Отсюда 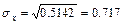и и 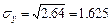коэффициент корреляции

.

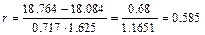Для составления уравнений прямых регрессии определяем коэффициенты регрессии:

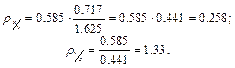
Таким образом, уравнение прямой регрессии у по х

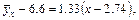или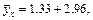

а уравнение прямой регрессии х по у

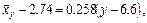или

Сравнение коэффициента корреляции в этом примере с коэффициентом корреляции в ранее рассмотренном примере распределения растений житняка

показывает на большую тесноту связи между, общим весом и весом семян. Это согласуется со структурой соответствующих корреляционных таблиц. Табл. 1 распределения растений житняка характерна четким смещением рядов распределения значений у при малой степени рассеяния этих значений, а табл. 6 по сахаропесочным заводам дает малозаметное смещение рядов распределения значений у при значительной степени рассеяния этих значений.

Дата добавления: 2014-12-26