
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЗАНЯТИЕ 7. Кривые второго порядка: окружность, эллипс, гипербола, парабола. Общие свойства кривых второго порядка. 2 страница
|
|
|
|
Директрисы гиперболы 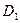 и
и 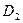 определяются параметром
определяются параметром  . Асимптоты гиперболы определяют выражения:
. Асимптоты гиперболы определяют выражения: 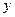 = ±
= ± 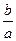
 .
.
Замечание: для принятого расположения фокусов ось 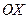 называют действительной осью гиперболы, ось
называют действительной осью гиперболы, ось 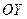 – мнимой осью.
– мнимой осью.
••• ≡ •••
Пример 5 – 265: Задано уравнение линии второго порядка:  . Показать, что линия есть гипербола, записать её каноническое уравнение. Найти: а) полуоси, б) координаты фокусов, в) эксцентриситет, г) уравнения директрис и асимптот.
. Показать, что линия есть гипербола, записать её каноническое уравнение. Найти: а) полуоси, б) координаты фокусов, в) эксцентриситет, г) уравнения директрис и асимптот.
Решение:
1). Перепишем уравнение: 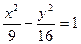 – это каноническое уравнение гиперболы с фокусами, расположенными на оси
– это каноническое уравнение гиперболы с фокусами, расположенными на оси 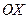 .
.
2). Полуоси гиперболы:  =3,
=3,  =4. Вычислим:
=4. Вычислим: 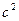 =
= 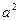 +
+ 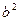 =25. Это значит:
=25. Это значит: 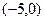 =
= 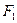 – левый фокус,
– левый фокус, 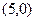 =
= 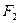 – правый фокус. Вычислим эксцентриситет:
– правый фокус. Вычислим эксцентриситет: 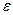 =
= 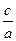 =
= 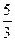 . Вычислим параметр директрисы:
. Вычислим параметр директрисы:  =
= 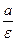 =
= 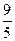 . Уравнения директрис
. Уравнения директрис 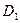 :
:  =–
=– 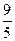 ,
, 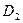 :
:  =
= 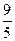 . Уравнения асимптот выражением:
. Уравнения асимптот выражением: 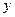 = ±
= ± 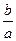
 = ±
= ± 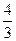
 .
.
Ответ: а) уравнение гиперболы 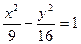 ,
,  =3,
=3,  =4; б) фокусы
=4; б) фокусы 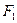 =
= 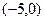 ,
, 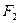 =
= 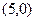 ; в) эксцентриситет
; в) эксцентриситет 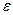 =
= 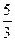 ; г) директрисы
; г) директрисы 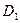 :
:  =–
=– 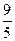 ,
, 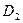 :
:  =
= 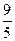 , асимптоты:
, асимптоты: 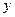 = ±
= ± 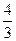
 .
.
Пример 6 – 269: Задано уравнение 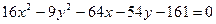 линии второго порядка. Показать, что линия есть гипербола, найти её центр и записать её каноническое уравнение. Найти: а) полуоси, б) координаты фокусов, в) эксцентриситет, г) уравнения директрис и асимптот.
линии второго порядка. Показать, что линия есть гипербола, найти её центр и записать её каноническое уравнение. Найти: а) полуоси, б) координаты фокусов, в) эксцентриситет, г) уравнения директрис и асимптот.
Решение:
1). Перепишем уравнение: 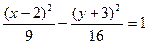 – это каноническое уравнение гиперболы с фокусами, расположенными на прямой линии
– это каноническое уравнение гиперболы с фокусами, расположенными на прямой линии 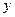 =3, с центром в точке (2,–3).
=3, с центром в точке (2,–3).
2). Воспользуемся параллельным переносом системы координат:  ,
, 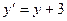 . Тогда уравнение принимает канонический вид, для которого все величины можно переписать из Примера 5-265. Полуоси гиперболы:
. Тогда уравнение принимает канонический вид, для которого все величины можно переписать из Примера 5-265. Полуоси гиперболы:  =3,
=3,  =4. Вычислим:
=4. Вычислим: 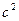 =
= 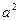 +
+ 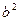 =25. Это значит:
=25. Это значит: 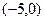 =
= 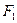 – левый фокус,
– левый фокус, 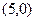 =
= 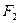 – правый фокус. Вычислим эксцентриситет:
– правый фокус. Вычислим эксцентриситет: 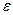 =
= 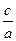 =
= 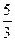 . Вычислим параметр директрисы:
. Вычислим параметр директрисы:  =
= 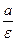 =
= 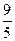 . Уравнения директрис
. Уравнения директрис 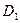 :
: 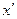 =–
=– 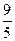 ,
, 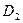 :
: 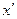 =
= 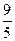 . Уравнения асимптот выражением:
. Уравнения асимптот выражением: 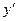 = ±
= ± 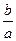
 = ±
= ± 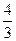
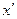 .
.
|
|
|
3). Учитывая  ,
, 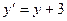 , запишем уравнения для старой системы координат: для директрис
, запишем уравнения для старой системы координат: для директрис 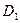 :
:  =
= 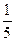 ,
, 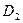 :
:  =
=  и для асимптот
и для асимптот 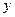 +3 = ±
+3 = ± 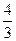
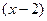 . Фокусы:
. Фокусы: 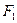 =
= 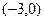 ,
, 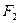 =
= 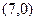 .
.
Ответ: а) уравнение гиперболы 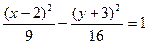 ,
,  =3,
=3,  =4; б) фокусы
=4; б) фокусы 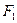 =
= 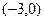 ,
, 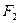 =
= 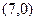 ; в) эксцентриситет
; в) эксцентриситет 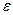 =
= 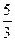 ; г) директрисы
; г) директрисы 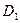 :
:  =
= 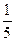 ,
, 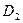 :
:  =
=  , асимптоты:
, асимптоты: 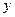 +3 = ±
+3 = ± 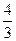
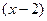 .
.
☺ ☻ ☺
Парабола: геометрическое место точек плоскости, для каждой из которых расстояние до данной точки плоскости, называемой фокусом, равно расстоянию до данной прямой, называемой директрисой.
В соответствии с определением параболы, отметим на плоскости 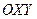 точку
точку 
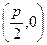 – фокус и прямую
– фокус и прямую 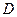 :
:  =
=  – директрису:
– директрису:
 Используя принятые на рисунке обозначения, в соответствии принятым определением параболы
Используя принятые на рисунке обозначения, в соответствии принятым определением параболы 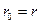 , легко получают каноническое уравнение параболы
, легко получают каноническое уравнение параболы  . (17)
. (17)
Для параболы имеем:  – эксцентриситет.
– эксцентриситет.
Замечание: рисунок и расположение директрисы и фокуса соответствуют случаю, когда 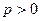 и осью параболы является ось
и осью параболы является ось 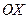 .
.
••• ≡ •••
Пример 7 – 285: Построить параболы: 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  . Найти параметр для каждой параболы.
. Найти параметр для каждой параболы.
Решение:
1). Перепишем уравнение:  . Имеем параболу с параметром
. Имеем параболу с параметром  =2, причём график заданной параболы – это график параболы
=2, причём график заданной параболы – это график параболы  , смещённый вправо на 2.
, смещённый вправо на 2.
2). Из уравнения:  следует, что осью параболы является ось
следует, что осью параболы является ось 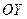 . Имеем параболу с параметром
. Имеем параболу с параметром  =
= 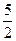 , ветви параболы направлены вверх.
, ветви параболы направлены вверх.
3). Из уравнения:  следует, что осью параболы является ось
следует, что осью параболы является ось 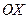 . Имеем параболу с параметром
. Имеем параболу с параметром  =–2, причём график заданной параболы – это график параболы
=–2, причём график заданной параболы – это график параболы  , симметрично отображённый относительно оси
, симметрично отображённый относительно оси 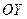 .
.
4). Из уравнения:  следует, что осью параболы является ось
следует, что осью параболы является ось 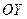 . Имеем параболу с параметром
. Имеем параболу с параметром  =–
=– 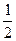 , причём график заданной параболы – это график параболы
, причём график заданной параболы – это график параболы 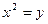 , симметрично отображённый относительно оси
, симметрично отображённый относительно оси 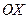 .
.
•◄ Дополнительно ►•
Пример 8 – 274. Записать уравнение гиперболы, если известно, что её фокусами являются точки 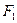 =(–3,–4) и
=(–3,–4) и 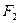 =(3,4), а расстояние между директрисами равно 3,6.
=(3,4), а расстояние между директрисами равно 3,6.
 Решение:
Решение:
1). Легко заметить, что точки 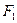 и
и 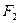 расположены симметрично относительно начала координат и расстояние между ними равно 10. Так как известно, что заданная кривая есть гипербола, то воспользуемся системой координат
расположены симметрично относительно начала координат и расстояние между ними равно 10. Так как известно, что заданная кривая есть гипербола, то воспользуемся системой координат  , в которой фокусы
, в которой фокусы  и
и 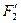 гиперболы располагаются на оси
гиперболы располагаются на оси  и имеют координаты:
и имеют координаты:  (–5,0) и
(–5,0) и 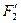 (5,0).
(5,0).
|
|
|
2). Так как параметр директрисы  =
= 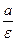 =
=  , то из условия:
, то из условия: 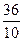 =
=  запишем
запишем 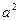 =9. Теперь можем вычислить:
=9. Теперь можем вычислить: 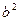 =
= 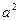 –
– 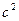 =16 и записать каноническое уравнение гиперболы в системе координат
=16 и записать каноническое уравнение гиперболы в системе координат  :
: 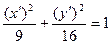 .
.
3). Система координат  получена из системы координат
получена из системы координат 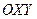 поворотом относительно точки
поворотом относительно точки 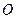 на угол
на угол 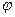 , такой что:
, такой что: 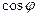 =
= 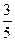 и
и 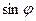 =
= 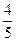 . Воспользуемся формулами перехода:
. Воспользуемся формулами перехода:  →
→ 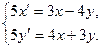 (S)
(S)
Подставляя (S) в каноническое уравнение гиперболы:  достаточно просто получаем уравнение заданной гиперболы в координатах
достаточно просто получаем уравнение заданной гиперболы в координатах  :
:  .
.
Ответ: уравнение гиперболы:  .
.
Пример 9 – 293. Записать уравнение касательной к параболе  , параллельной прямой линии:
, параллельной прямой линии:  .
.
Решение:
1). Перепишем уравнение касательной: 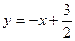 . Отсюда получаем угловой коэффициент касательной:
. Отсюда получаем угловой коэффициент касательной:  =–1.
=–1.
Замечание: можно было бы воспользоваться универсальными средствами математического анализа и выделить на параболе точку, в которой 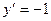 .
.
2). Воспользуемся готовым уравнением касательной к параболе в точке  , именно:
, именно:  →
→  .
.
3). В нашем случае  =4. Тогда для точки
=4. Тогда для точки  получаем:
получаем: 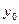 =–1. Из равенства:
=–1. Из равенства:  получаем
получаем 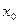 =2. Можем записать уравнение касательной:
=2. Можем записать уравнение касательной:  .
.
Ответ: уравнение касательной:  .
.
☻
Вопросы для самопроверки:
1. Что такое окружность, эллипс?
2. Что такое гипербола?
3. Что такое парабола?
4. Что такое эксцентриситет кривой второго порядка?
5. Что такое директриса для кривой 2-го порядка?
< * * * * * >
Задачи для самоподготовки:
Пример C7 – 1: Написать уравнение диаметра окружности: 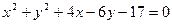 , перпендикулярного прямой линии
, перпендикулярного прямой линии  :
: 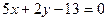 .
.
Ответ: уравнение диаметра  :
:  .
.
Пример C7 – 2: Написать каноническое уравнение эллипса, если известно, что: 1)  =3,
=3,  =2; 2)
=2; 2)  =5,
=5, 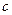 =4; 3)
=4; 3) 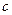 =3,
=3, 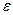 =
=  ; 4)
; 4)  =5,
=5, 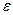 =
=  ; 5)
; 5) 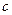 =2, 2
=2, 2  =5; 6)
=5; 6) 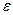 =
= 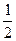 , 2
, 2  =32.
=32.
Ответ: для случаев: 1) 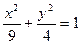 , 2)
, 2)  , 3)
, 3)  , 4)
, 4) 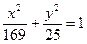 .
.
5)  , 6)
, 6)  .
.
Пример C7 – 3: На эллипсе: 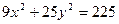 найти точку, расстояние которой до фокуса
найти точку, расстояние которой до фокуса 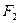 в 4 раза больше расстояния до фокуса
в 4 раза больше расстояния до фокуса 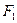 .
.
Ответ: точка: 
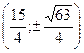 .
.
Пример C7 – 4: Написать уравнение кривой, по которой движется точка 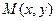 , если расстояние её до точки
, если расстояние её до точки  (3,0) остаётся в 2 раза меньше расстояния до прямой линии
(3,0) остаётся в 2 раза меньше расстояния до прямой линии  :
:  .
.
Ответ: уравнение кривой линии 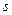 :
:  .
.
Пример C7 – 5: Задано уравнение линии второго порядка: 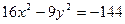 . Показать, что линия есть гипербола, записать её каноническое уравнение. Найти: а) полуоси, б) координаты фокусов, в) эксцентриситет, г) уравнения директрис и асимптот.
. Показать, что линия есть гипербола, записать её каноническое уравнение. Найти: а) полуоси, б) координаты фокусов, в) эксцентриситет, г) уравнения директрис и асимптот.
|
|
|
Ответ: а) уравнение гиперболы  ,
,  =4,
=4,  =3; б) фокусы
=3; б) фокусы 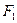 =
= 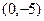 ,
, 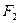 =
= 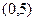 ; в) эксцентриситет
; в) эксцентриситет 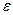 =
=  ; г) директрисы
; г) директрисы 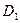 :
:  =–
=– 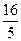 ,
, 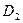 :
:  =
= 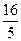 , асимптоты:
, асимптоты: 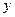 = ±
= ± 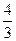
 .
.
Пример C7 – 6: Задано уравнение  линии второго порядка. Показать, что линия есть гипербола, найти её центр и записать её каноническое уравнение. Найти: а) полуоси, б) координаты фокусов, в) эксцентриситет, г) уравнения директрис и асимптот.
линии второго порядка. Показать, что линия есть гипербола, найти её центр и записать её каноническое уравнение. Найти: а) полуоси, б) координаты фокусов, в) эксцентриситет, г) уравнения директрис и асимптот.
Ответ: а) уравнение гиперболы 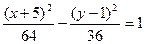 ,
,  =8,
=8,  =6; б) фокусы
=6; б) фокусы 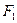 =
= 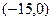 ,
, 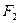 =
= 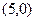 ; в) эксцентриситет
; в) эксцентриситет 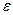 =
=  ; г) директрисы
; г) директрисы 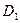 :
:  =–
=–  ,
, 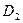 :
:  =
=  , асимптоты:
, асимптоты: 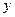 –1 = ±
–1 = ± 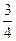
 .
.
Пример C7 – 7: Написать уравнение параболы с вершиной в начале координат, если известно, что: 1) парабола расположена в левой полуплоскости симметрично оси 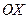 и
и  =
= 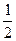 ; 2) парабола расположена симметрично оси
; 2) парабола расположена симметрично оси 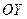 и проходит через точку
и проходит через точку 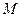 (4,–8); 3) фокус параболы расположен в точке
(4,–8); 3) фокус параболы расположен в точке  (0,–3).
(0,–3).
Ответ: параболы: 1)  , 2)
, 2)  , 2)
, 2) 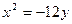 .
.
< * * * * * >
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 1458; Нарушение авторских прав?; Мы поможем в написании вашей работы!