Кинематика сплошной среды

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Гагуа Е.Д. Тренировка спринтера / Е.Д. Гагуа. – М.: Олимпия Пресс, Терра-Спорт, 2001. – 72 с.

2. Жилкин А.И. Легкая атлетика: учеб. пособ. для высш. пед. учеб. заведений / А.И. Жилкин, В.С. Кузьмин, Е.В. Сидорчук. – М.: Академия, 2003. – 464 с.

3. Легкая атлетика и методика преподавания: учеб. для ин-тов физ. культ. / под ред. О.В. Колодия, Е.М. Лутовского, В.В. Ухова. – М.: Физкультура и спорт, 1985. – 271 c.

4. Легкая атлетика. Правила соревнований / под ред. В.И. Лахова [и др.] – М.: Всероссийская федерация легкой атлетики, 1994. – 176 с.

5. Легкая атлетика. Правила соревнований. 2006-2007 / Международная Ассоциация легкоатлетических федераций; под общ. ред. В. Зеличенка; перев. А. Гнетовой. – М.: Тера-Спорт, Олимпия Пресс, 2006. – 144 с.

6. Легкая атлетика: учеб. для ин-тов физ. культ. / Под ред. Н.Г. Озолина, В.И. Воронкина, Ю.Н. Примакова. – Изд. 4-е, доп., перераб. – М.: Физкультура и спорт, 1989. – 671 с.

7. Попов В.Б. Прыжок в длину: многолетняя подготовка / В.Б. Попов. – М.: Олимпия Пресс, Терра-Спорт, 2001. – 160 с.

8. Тер-Ованесян И.А. Подготовка легкоатлета: современный взгляд / И.А. Тер-Ованесян. – М.: Терра-Спорт, 2000. – 128 с.

9. Учебник тренера по легкой атлетике / под ред. Л.С. Хоменкова. – Изд. 2-е, перераб. и доп. – М.: Физкультура и спорт, 1982. – 479 с.

10. Шур М. Прыжок в высоту: учебно-методическое издание / М. Шур. – М.: Тера-Спорт, 2003. – 144 с.

Задача кинематики - описание движения среды независимо от внешних условий, которые инициируют и поддерживают движение. Т.к. сплошная среда представляет собой непрерывную совокупность точек, то чтобы описать её движение, необходимо описать движение всех точек. Поэтому вернёмся к некоторым понятиям теоретической механики, изучающей движение точки.

3.1. ДВИЖЕНИЕ ТОЧКИ С ПОЗИЦИЙ ТЕОРЕТИЧЕСКОЙ

МЕХАНИКИ

Траектория движущейся точки. Движение материальной точки мы рассматриваем в теоретической механике. В этом случае, для описания полного движения точки необходимо знать уравнение её движения т.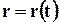е. , где 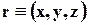- радиус-вектор точки. Чтобы найти скорость точки надо взять производную от правой части уравнения движения.

Рассмотрим движение точки в некоторой определённой системе прямоугольных и прямолинейных координат Oxyz, которую условимся называть неподвижной.

Кривая, описываемая последовательными положениями движущейся точки, называется траекторией.

Аналитически движение точки определено, если заданы её координаты x, y, z, как непрерывные функции времени t:

x = j₁ (t); y = j₂(t); z = j₃(t).

Эти уравнения определяют положение движущейся точки в каждый момент времени t и представляют в параметрической форме уравнение траектории. Если на траектории выбрать точку М₀, от которой отсчитывать длину дуги s траектории до движущейся точки М, то движение М определяется законом изменения s, как функции времени t:

s = s (t).

Перемещение. Скорость. Пусть М и М¢ - положения движущейся точки, отвечающие соответственно моментам t и t + Dt. Вектор 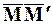называется перемещением точки за промежуток времени Dt. Этот вектор с началом в точке М представляет собой хорду, стягивающую положения движущейся точки в моменты t и t + Dt.

Перемещение 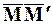разделим на Dt; вектор

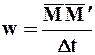
называется средней скоростью точки М за промежуток времени Dt.

Средняя скорость есть вектор, приложенный в точке М и имеющий то же направление, что и перемещение .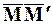

Предел средней скорости, когда Dt стремится к 0, называется скоростью точки М в момент t и обычно обозначается

.

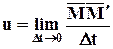В пределе направление хорды совпадает с направлением касательной к траектории; поэтому скорость u точки М представляет собой вектор, приложенный в точке М и направленный по касательной к траектории в сторону движения.

Положение точки М можно определить вектором 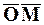, выходящим из начала координат О. Перемещение 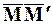за промежуток времени Dt равно приращению 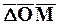вектора :

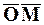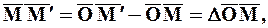
откуда

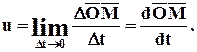
Таким образом, скорость движущейся точки равна производной по времени от радиуса-вектора движущейся точки и представляет собой вектор, приложенный в движущейся точке.

Проекции скорости на оси координат. Пусть x, y, z координаты точки М, а x + Dx, y +Dy, z +Dz - координаты точки 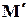. Проекции перемещения 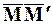на оси координат будут соответственно равны Dx, Dy, Dz; проекции средней скорости w будут

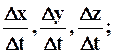
отсюда проекции истинной скорости u на оси координат Oxyz будут пределами предыдущих выражений при Dt® 0, или

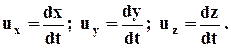
Теорема. Проекции скорости на прямоугольные оси равны первым производным по времени от соответствующих координат движущейся точки.

Так как оси Oxyz ортогональны, величина скорости определится через проекции формулой:

.

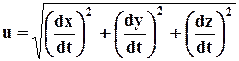Если через s обозначить длину дуги траектории, отсчитываемой от неподвижной точки, то

.

Следовательно, алгебраическая величина скорости будет определяться формулой

.

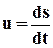При этом, если u положительна, то скорость направлена в сторону возрастающих значений s. Движение называется равномерным, если величина скорости постоянна. Тогда

Допустим, что s₀ есть значение s для начального момента времени t = 0; тогда, интегрируя предыдущее выражение, получаем: s = s₀ + at.

То есть, в равномерном движении пройденные пути пропорциональны времени. Величина скорости равна пути, пройденному в равномерном движении за единицу времени.

Теорема о проекции скорости. Возьмём ось х за траекторию движения (если движение прямолинейное). Значит s = х, и уравнение движения имеет вид: x = f(t). Алгебраическая величина скорости точки, движущейся по оси х, представляется формулой

v = dx/dt = f¢(t).

Но, при движении точки в пространстве, dx/dt есть проекция её скорости на ось х; в то же время эта величина равна скорости ортогональной проекции М₁ точки М на ось х, так как х есть абсцисса точки М₁.

Следовательно, если спроектировать на неподвижную ось движущуюся точку и её скорость, то проекция скорости будет равна скорости проекции.

3.2. МЕТОДЫ ОПИСАНИЯ ДВИЖЕНИЯ СПЛОШНОЙ СРЕДЫ

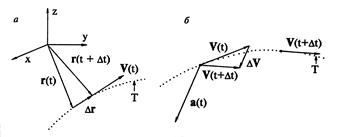Рис. 3.1. Скорость и ускорение материальной точки. Пунктиром показана её траектория

При изучении движения сплошной среды можно также выделить бесконечно малые объёмы, положение которых характеризуется в пространстве тремя координатами или величиной одного радиус-вектора 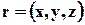, и рассматривать движение сплошной среды как движение совокупности взаимно связанных и взаимодействующих бесконечно малых (точечных) объёмов.

Метод Лагранжа. Обозначим координаты начального (в момент времени 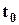) положения каждой точки сплошной среды через 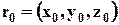. Для полного описания движения сплошной среды необходимо знать траектории движения всех частиц, т.е. положение каждой частицы в любой момент времени 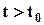. Это означает, что для каждой частицы надо знать уравнение её траектории . При этом одну частицу от другой отличает начальное положение частицы, и, следовательно, величина 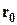войдёт в уравнение траектории жидкой частицы как параметр:

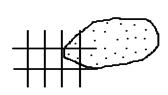Рис.3.2. Задание координат методом Лагранжа

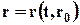. (3.2.1)

Такой подход к описанию движения сплошной среды называется методом Лагранжа, а характеристики сплошной среды (скорость, плотность, давление и т.п.), связанные с движущимися элементарными объёмами сплошной среды, равно как и координаты этого объёма, называются лагранжевыми переменными.

Лагранжевы координаты - это параметры, которые характеризуют каждую точку среды и не меняются в процессе. Таким образом, точка зрения Лагранжа опирается на описание истории движения каждой точки сплошной среды в отдельности. Такое описание на практике оказывается слишком подробным и сложным, оно всегда подразумевается при формулировке физических законов.

Используя равенства, введённые в теоретической механике

,

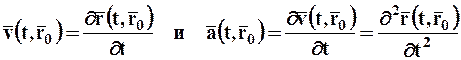можно вычислить скорость и ускорение каждой частицы, а затем, определив величину внешних (поверхностных и объёмных) сил, действующих на каждую частицу, записать уравнения движения для сплошной среды.

Несмотря на кажущуюся простоту метода Лагранжа, уравнения движения, получаемые на основе этого метода, очень сложны, и он используется сравнительно редко.

Более удобен и потому гораздо шире используется другой подход к описанию движения сплошной среды, называемый методом Эйлера.

Согласно этому методу фиксируют не частицы жидкости, а точки пространства, через которые проходят в разные моменты времени различные элементарные объёмы жидкости, т.е. жидкие частицы. В этих точках определяются значения скорости движения сплошной среды. Таким образом, средством описания движения сплошной среды является поле скорости движения жидких частиц в фиксированных точках пространства:

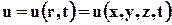. (3.2.2)

Характеристики сплошной среды (поле скорости, поле давлений, поле напряжений и т.п.), отнесённые к фиксированным неподвижным элементам геометрического пространства (точкам, линиям, поверхностям, объёмам), и сами эти элементы называют эйлеровыми переменными.

Этот метод удобен благодаря следующим преимуществам.

· Во-первых, наблюдать за движущимися (например, в трубе) фиксированными (мечеными) жидкими частицами значительно сложнее, чем за характеристиками движения сплошной среды.

· Во-вторых, соответствующие этому методу уравнения оказываются проще для анализа.

Подчеркнём, что, если в методе Лагранжа 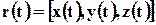- это искомые функции времени, то в методе Эйлера пространственные координаты 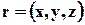- не функции времени, а независимые переменные, декартовы координаты пространства, в котором перемещается сплошная среда. Искомыми переменными являются скорость 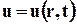и давление .

Учитывая, что в методе Эйлера описание движения отличается от принятого в теоретической механике, существуют некоторые отличия в определении ускорения, которое входит во второй закон Ньютона. В это уравнение входит ускорение материальной точки, которое для сплошной среды определяется, как и в теоретической механике, второй производной пути по времени только при использовании метода Лагранжа. В случае метода Эйлера ускорение, а также другие гидромеханические величины, которые меняются вместе с движением объёма жидкости, выражаются через специальный вид производной, которая определённым образом связана с полем скорости (3.2.2). Вместе с тем эта производная должна быть связана с движением частиц жидкости или газа (субстанции). Такую производную называют полной или субстанциальной.

Скорость. Пусть некоторая точка сплошной среды в момент t находится в точке М пространства, а в момент t + Dt в точке M´, и 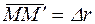. Dr -малоенаправленноеперемещениеиндивидуальнойточки сплошной среды за время Dt (если в пространстве можно ввести радиус-вектор, то это приращение радиус-вектора рассматриваемой точки сплошной среды). Предел отношения двух соответствующих бесконечно малых количеств Dr и Dt при Dt® 0 (в случае неевклидова пространства) или частная производная радиуса-вектора точки сплошной среды относительно системы отсчёта по времени 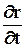(в случае евклидова пространства) называется скоростью точки сплошной среды.

Радиус-вектор r зависит в общем случае от трёх параметров x, y, z, индивидуализирующих точку сплошной среды, и времени t. Скорость вычисляется для индивидуальной точки сплошной среды, т.е. при фиксированных x, y, z, поэтому и берётся частная производная от r по t: 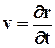. Бесконечно малое перемещение точки сплошной среды 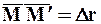можно разложить по векторам базиса, взятым в точке М:

Dr = Dx×i + Dy×j + Dz×k,

где Dx, Dy, Dz являются компонентами перемещения Dr. Или, переписывая в обобщённом и сокращённом виде, будем иметь

Dr = S Dxⁱ е_i = Dxⁱ е_i (*)

(В последнем выражении знак суммы опущен).

Поделив (*) на элемент времени Dt, соответствующий перемещению точки сплошной среды из точки М в точку M´ пространства наблюдателя, и взяв предел при Dt® 0, получим по определению скорость точки сплошной среды: ,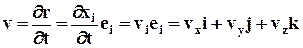

откуда ,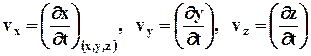

индексы 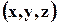внизу указывают на то, что производные берутся при постоянных параметрах, индивидуализирующих точку среды. Величины v_x, v_y, v_z называются компонентами вектора скорости v в базисе i, j, k. Скорость и её компоненты зависят от x, y, z, t:

v_x = v_x (x, y, z, t),

v_y = v_y (x, y, z, t),

v_z = v_z (x, y, z, t).

Запишем проекции скоростей и ускорений точек среды на обобщённые оси координат х_i, которые определяются обычными равенствами:

,

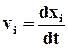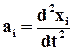. (3.2.3)

Таким образом, в методе Эйлера задаются перемещение, скорость, ускорение в точке пространства (неподвижная система отсчёта), мимо которой в данный момент проходят частицы среды как функции координат точек пространства x_i и времени t:

u_i = u_i (x₁, x₂, x₃ , t);

v_i = v_i (x₁, x₂, x₃ , t);

а_i = a_i (x₁, x₂, x₃ , t). (3.2.4)

Совокупность параметров х_i и t называют переменными Эйлера.

Ввиду того, что в механике сплошной среды могут встретиться оба метода, необходимо научиться осуществлять переход от одних переменных к другим.

Переход от переменных Лагранжа к переменным Эйлера. Предположим, что у нас всё известно о среде с точки зрения Лагранжа, то есть, мы имеем 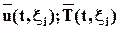и закон движения в соответствующей форме:

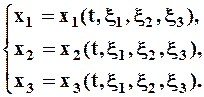
Для того, чтобы перейти к переменным Эйлера нам необходимо:

· разрешить уравнения относительно x_i. При фиксированных координатах х_i эти соотношения указывают те точки x_i сплошной среды, которые в разные моменты времени проходят через данную точку пространства.

x_i = x_i(x₁, x₂, x₃ , t)

или

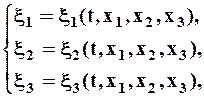(3.2.5)

· подставить это в выражения по Эйлеру:

.

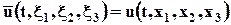Рис. 3.3. Переход от координат Эйлера к координатам Лагранжа

Для перехода от переменных Эйлера к переменным Лагранжа имеем:

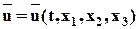(*), проекция которой на ось х₂ равна 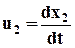, а проекция на ось х₃ равна .

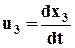Для начальных условий при t = 0:

,

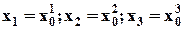откуда

· получим систему обыкновенных дифференциальных уравнений относительно х_i: 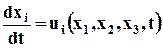или

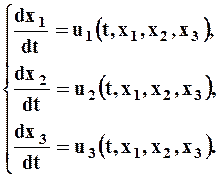
· Решая эту систему, определим х_i = х_i(С₁, С₂, С₃, t), где - С₁, С₂, С₃ -постоянные, определяемые по х_i при t = t_0;

· подставив (**) в (*), получим лагранжевы координаты.

.

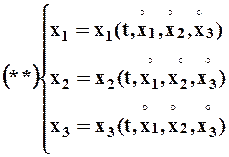Ускорение и его вычисление по скорости. Ускорение – это скорость изменения скорости индивидуальной частицы. Если скорость задана по Лагранжу, т.е.

.

Если скорость задана по Эйлеру, то В индивидуальной частице: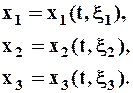

Поэтому 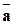по формуле дифференцирования сложной функции

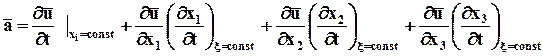
Окончательная формула по Эйлеру будет выглядеть:

.

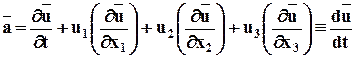Это полная (материальная) производная скорости по времени, индивидуальная производная по времени, субстанциальная производная.

По Эйлеру 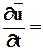производная по времени при x_i = const – изменение скорости по времени в данном месте пространства – локальная производная по времени.

Если 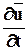=0, то движение установившееся (стационарное):

.

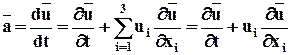В декартовых координатах x,y,z:

.

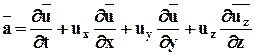В проекциях

;

;

.

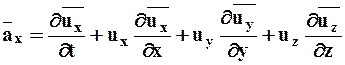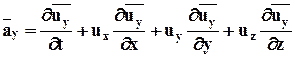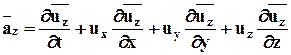Материальная (полная) или индивидуальная производная по t от любой величины (например, плотности r) определится следующим образом:

· Если используется способ Лагранжа, т.е. если 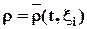, то индивидуальная производная есть частная .

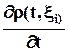· Если используется способ Эйлера, т.е. 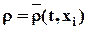, то индивидуальная производная есть

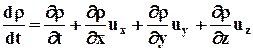или = .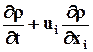

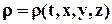Для несжимаемой среды 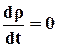, при этом 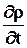может быть и не равно 0 (т.к.среда неоднородная).

Таким образом, если функция задана в переменных Эйлера: r = r (x₁, x₂, x₃, t), необходимо

· перейти к переменным Лагранжа;

· воспользоваться правилом дифференцирования сложной функции, в результате чего получим

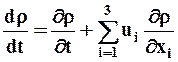. (3.2.6)

Производная 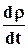называется полной производной (индивидуальной, субстанциальной) и характеризует изменение плотности данной частицы сплошной среды в единицу времени. Производная 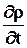называется частной (местной, локальной) и характеризует изменение плотности в данной точке пространства в единицу времени. Величина 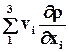называется конвективной производной.

Рассмотрим полную производную по времени от температуры. По Эйлеру это будет выглядеть следующим образом:

Дата добавления: 2014-12-26