Сверхзвуковым потоком

Рассмотрим осесимметричное обтекание конуса с углом полураствора 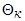сверхзвуковым потоком. Решение этой задачи используется, в частности, для определения коэффициента волнового сопротивления конических носовых частей корпусов ЛА.

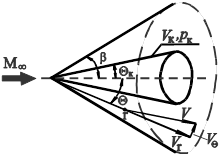Рис. 20. Осесимметричное обтекание острого конуса

При симметричном обтекании конуса с углом полураствора 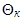, удовлетворяющим условию , на нем возникает присоединенный конический скачок уплотнения с вершиной в вершине конуса (рис. 20). Тогда задача расчета обтекания конуса сводится к нахождению угла полураствора конического скачка 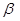и поля скоростей (и давлений) между скачком уплотнения и конусом. Скачок уплотнения имеет прямолинейную образующую, поэтому при переходе через фронт скачка по всем линиям тока энтропия возрастает одинаково (потери механической энергии одинаковы) и течение около конуса за скачком является изоэнтропическим. Задача решается в полярной системе координат с полюсом в вершине конуса. Течение в области между конусом и скачком уплотнения является коническим, то есть обладающим следующим свойством: параметры течения на поверхности любого промежуточного конуса постоянны и меняются лишь при переходе с одной конической поверхности на другую.

Для определения поля скоростей имеем систему двух обыкновенных дифференциальных уравнений, в которых неизвестными являются только составляющие скорости и .

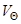. (3.4)

Для решения задачи необходимо задать граничные условия:

1. На поверхности конуса нормальная составляющая скорости равна нулю (условие непротекания через поверхность)

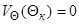. (3.5)

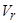2. На поверхности скачка уплотнения составляющие скорости и должны удовлетворять основным соотношениям для косого скачка уплотнения (рис. 21):

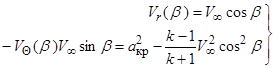. (3.6)

Условия (3.6) можно свести к одному для составляющих скорости и 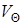за скачком уплотнения, исключив из них :

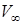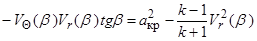. (3.7)

  Рис. 21. Треугольники скоростей для косого скачка уплотнения.

Здесь за положительное направление 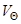принято направление в сторону увеличения угла 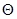. Заметим, что угол в условии (3.7) неизвестен и находится в процессе решения задачи.

Система дифференциальных уравнений (3.4) при граничных условиях (3.5) и (3.7) может быть решена численно методом конечных разностей. Численное интегрирование системы дифференциальных уравнений можно начать с поверхности конуса (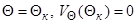), задаваясь величиной скорости потока 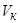на поверхности конуса, или с поверхности скачка уплотнения, задаваясь углом 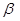при данном . В первом случае в результате решения должны быть найдены соответствующие заданной скорости 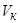число , угол наклона скачка и поле скоростей между конусом и скачком уплотнения, а во втором случае – угол 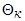и скорость на промежуточных конусах.

Для численного интегрирования вводят в рассмотрение безразмерные составляющие скорости и скорости звука:

.

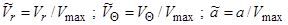В записи через конечные разности система дифференциальных уравнений (3.4) принимает вид

, (3.8)

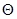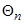где – приращение угла , – угол промежуточного конуса 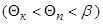. Если расчет начинается с поверхности скачка уплотнения, то (при 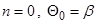), если с поверхности конуса, то 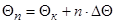(при ).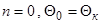

При расчете с поверхности конуса с углом 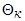задаемся относительной скоростью 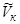на его поверхности, приращением и переходим от поверхности конуса к промежуточному конусу 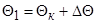. Получим

,

так как 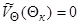, а , затем находим составляющую скорости :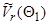

.

Далее, зная 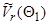и , из второго уравнения системы (3.8) определяем , а из первого – 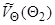, где 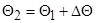, и т.д. Интегрирование продолжается до тех пор, пока не будет выполняться условие на скачке уплотнения (3.7), которое для составляющих скорости, отнесенных к , имеет вид

.

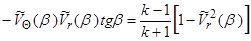Угол наклона скачка будет равен углу того промежуточного конуса 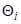, для которого выполняется это условие.

Анализ результатов расчета показывает, что каждому углу конуса теоретически соответствуют два решения. Одно дает меньшую скорость и больший угол наклона скачка, другое наоборот – большую скорость и меньший угол скачка. Как показывают исследования, реальным для присоединенного конического скачка является второе решение (как и в случае плоского течения).

Зная и составляющую за скачком уплотнения, рассчитываем:

а) число

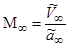, где и ,

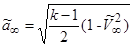; (3.9)

б) отношение давления 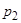за скачком уплотнения к давлению 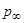набегающего потока по известному соотношению для косого скачка уплотнения

, (3.10)

Угол наклона скачка можно определить с помощью рис. 3 прил. по величине и углу конуса 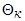. Давление на поверхности конуса рассчитывается по формуле изоэнтропического течения

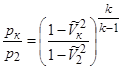, (3.11)

здесь .

Как известно, коэффициент волнового сопротивления конуса , отнесенный к площади миделя (здесь – к площади донного среза) равен коэффициенту давления на поверхности конуса

, где . (3.12)

В результате обработки данных точной теории для расчета коэффициента давления на конусе, т. е. коэффициента волнового сопротивления, получена приближенная формула

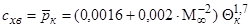, (3.13)

где угол 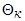– в градусах. Расчет по формуле (3.13) можно вести до значени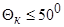й и 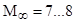. Нижний предел допустимых значени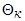й и определяется теми их значениями, при которых поток между конусом и скачком остается сверхзвуковым.

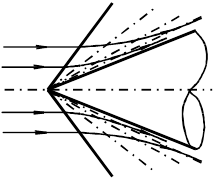Рис. 22. Форма линий тока в области за коническим скачком уплотнения

Отметим некоторые особенности обтекания конуса сверхзвуковым потоком в сравнении с клином. Перед конусом образуется конический скачок, присоединенный к вершине конуса, если угол раствора конуса меньше максимального значения для данной скорости набегающего потока. При одинаковых числах Маха и углах раствора конуса и клина скачок на конусе имеет меньший угол наклона, чем на клине, так как конус вызывает меньшее стеснение потока, чем клин бесконечного размаха того же угла раствора. При переходе через конический скачок линии тока, также как и в случае плоского скачка, претерпевают излом (рис. 22). Однако так как скачок на конусе слабее, чем на клине, непосредственно за скачком линии тока будут иметь наклон меньше, чем угол раствора конуса. В области между скачком уплотнения и конусом происходит плавный разворот линий тока. С удалением от скачка угол наклона линий тока увеличивается и асимптотически приближается к направлению, заданному образующей конуса. Как показывают расчеты, за коническим скачком происходит изоэнтропическое сжатие газа. В результате скорость газа плавно уменьшается, а давление возрастает, и параметры газа асимптотически приближаются к их значениям на поверхности конуса.

1.3.3. Несимметричное обтекание конуса сверхзвуковым потоком назад

Система уравнений

При сверхзвуковом обтекании конуса под углом атаки 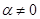поток около него будет обладать свойством конического течения с той особенностью, что параметры сохраняют постоянное значение не целиком на конической поверхности, а вдоль отдельных прямолинейных образующих конуса. Параметры в таком потоке изменяются при переходе от одной образующей, проходящей через вершину конуса, к другой. Такой конический поток обычно рассматривают в сферической системе координат (рис. 23), выбранной таким образом, что координате соответствует вершина конуса, оси координат (ось 3) – направление скорости набегающего потока, а меридиональной плоскости – плоскость, проходящая через ось 3 и ось 1 – ось симметрии конуса. В этой системе координат уравнение конуса, наклоненного к оси 3 под углом (на рис. 23 этот угол отрицательный), будет следующим:

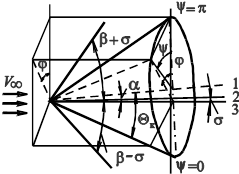Рис. 23. Схема потока около конуса, наклоненного под углом атаки (1 – ось конуса, 2 – ось скачка уплотнения, 3 – ось координат и направление )

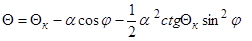(3.14)

где – сферическая координата для образующей конуса.

Из свойств конического потока следует, что значения его параметров не зависят от r, а являются функциями переменных и . Поэтому в уравнениях возмущенного течения отсутствуют производные по r. В случае несимметричного конического сверхзвукового потока течение в плоскости будет изоэнтропическим. Это объясняется тем, что вдоль линии пересечения этой плоскости с поверхностью скачка, представляющей собой прямую линию, энтропия будет постоянной, так как условия перехода газа через скачок будут одинаковыми для каждой линии тока. Такое же явление будет наблюдаться в любой другой плоскости . Однако в связи с тем, что наклон скачка неодинаков в каждой из этих плоскостей, неодинаковой будет и энтропия, являющаяся, таким образом, функцией угла . Из этого следует, что несимметричный конический поток за скачком оказывается неизоэнтропическим.

Теоретической основой для исследования такого потока являются уравнения движения идеальной среды и уравнение неразрывности в сферической системе координат (см., например, [9, с.49, 52, 137]). Решения системы дифференциальных уравнений находят в виде

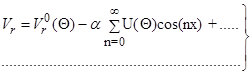(3.15)

Аналогичные выражения записывают и для остальных искомых параметров: составляющих скорости по соответствующим направлениям сферической системы координат и , давления 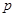, плотности 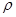. Здесь – параметры симметричного обтекания на промежуточном конусе с углом .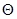

Каждое из уравнений (3.15) представляет собой ряд, в котором член, линейный по отношению к углу атаки, определяет решение в первом приближении, а квадратичный член – во втором. При малых углах значения параметров будут мало отличаться от соответствующих значений при симметричном обтекании, и влияние угла 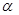достаточно учесть только линейными членами. С возрастанием 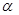становится необходимым вести расчет с учетом второго приближения, которым обычно и ограничиваются, полагая, что углы атаки не велики.

В рассматриваемых уравнениях коэффициенты 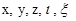можно рассматривать как величины, определяющие эффект угла атаки в первом приближении, а коэффициенты 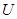и др. – во втором. Все эти коэффициенты зависят от одной переменной .

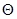Из выражений (3.15) следует, что определение параметров обтекания конуса под углом атаки начинается с решения частной задачи о симметричном потоке около того же конуса. В результате ее решения отыскивают значения в зависимости от угла 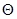. В дальнейшем рассматривают влияние угла атаки.

Задача о влиянии угла атаки в первом приближении сводится к определению коэффициентов 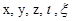рядов (3.15) при условии, что квадратичные и более высокие степени в них отсутствуют, при этом принимают n = 1. Тогда система (3.15) запишется так:

. (3.16)

Найденные в результате решения задачи коэффициенты x, y, z, отнесенные к максимальной скорости , а также безразмерные величины 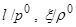затабулированы для различных конусов и чисел . Частично эти результаты приведены в табл. 11, 12 [9]. При их помощи по формулам (3.16) ведется расчет скорости, давления и плотности.

Приближенный метод расчета (метод местных конусов)

Для оценки параметров на поверхности несимметрично обтекаемого конуса можно непосредственно воспользоваться результатами, полученными для нулевого угла атаки.

Существо приближенного метода заключается в следующем. Предполагают, что каждая образующая конуса, отклоненного на некоторый угол 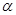, принадлежит условному конусу, симметрично обтекаемому тем же потоком. Этот конус, построенный на основе местной образующей с наклоном к направлению невозмущенного потока, называется местным конусом. Имея результаты теории симметричного обтекания, можно определить параметры на поверхности местного конуса, следовательно и на той образующей, которая принадлежит действительному конусу.

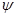Основным элементом предварительного расчета является значение угла местного конуса. Его величину можно получить из выражения (3.14). Однако лучшее соответствие результатов расчета параметрам течения получается в том случае, если вместо угла использовать угол . Угол рассчитывается по формуле

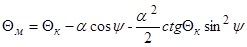, (3.17)

которая при значениях (подветренная сторона) и (наветренная сторона, рис. 22) дает те же результаты, что и формула (3.14), а для промежуточных значений 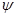– меньшие значения угла местного конуса.

В ходе расчета задаются углами 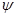, определяют для заданных фиксированных значений и соответствующие величины , а по ним, зная число , по теории симметричного обтекания определяют параметры на отклоненном конусе. Результаты расчета дают зависимости параметров на поверхности конуса от угла 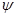. Наряду с этим можно найти параметры течения за скачком уплотнения и угол его наклона.

Погрешность этого метода оценивают путем сравнения результатов с точной теорией и экспериментальными данными. На образующих, принадлежащих нулевой меридианальной плоскости ( и 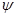равны 0 или 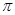), должно иметь место совпадение результатов. На промежуточных образующих (углы 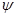отличны от 0 и 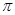) вследствие перетекания газа, обусловленного нарушением симметрии течения и не учитываемого в методе местных конусов, в соответствующих точках поверхности наблюдается отклонение вычисленных значений параметров от действительных. При этом с увеличением скорости и уменьшением угла атаки точность расчетов повышается. Поэтому целесообразно этот метод применять при достаточно больших скоростях и сравнительно малых углах атаки.

1.3.4. Приближенный метод расчета обтекания сверхзвуковым назад

Дата добавления: 2014-12-26