
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Итерационные методы для обратного интерполирования
|
|
|
|
Если функция y = f(x) задана таблицей с равноотстоящими узлами, то записываем для нее один из интерполяционных многочленов, например первый интерполяционный многочлен Ньютона:
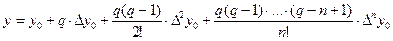 (5.4)
(5.4)
Рассматривая последнее выражение как уравнение относительно q, находим q по заданному значению y, а затем вычисляем x=x0+qh
Если число узлов велико, то получим алгебраическое уравнение высокой степени, при решении которого удобно применять метод итераций. Запишем уравнение (5.4) в виде
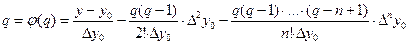 (5.5)
(5.5)
За начальное приближение принимаем 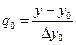 ,
,
а затем применяем процесс итерации 
В большинстве случаев при достаточно малом шаге h = xi+1-xi процесс итерации сходится к искомому корню. 
Условием сходимости является выполнение неравенства 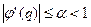
На практике считают до тех пор, пока два последовательных значения qk и qk+1 не совпадут с заданной точностью.
Пример 5.6 Используя таблицу значений функции y = sh x найти x при котором sh x=5.
Таблица 5.5.
Значения функции y = sh x
| x | y | Δy | Δ2y | Δ3y |
| 2.2 | 4.457 | 1.009 | 0.220 | 0.054 |
| 2.4 | 5.466 | 1.229 | 0.274 | 0.043 |
| 2.6 | 6.695 | 1.503 | 0.317 | |
| 2.8 | 8.198 | 1.820 | ||
| 3.0 | 10.018 |
Составляем первый интерполяционный многочлен Ньютона, останавливаясь на разностях третьего порядка, которые практически уже постоянны:

Полагаем x0 = 2.2, так как заданное значение y = 5 находится между y0 = 4.457 и y1 = 5.466. Итерирующая функция имеет вид
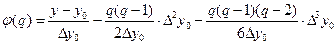
Начальное приближении

Затем последовательно находим

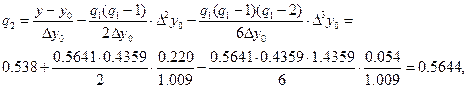
Таким образом, мы можем принять q = 0.564 и
x = 2.2+0.564*0.2 = 2.313
с точностью до 0.001.
Глава 6. Аппроксимация функций с помощью сплайнов
При большом количестве узлов интерполяции приходится использовать интерполяционные полиномы высокой степени, что создает определенные неудобства при вычислениях. Можно избежать высокой степени интерполяционного многочлена, разбив отрезок интерполяции на несколько частей с построением на каждой части самостоятельного интерполяционного многочлена. Однако такое интерполирование обладает существенным недостатком: в точках сшивки разных интерполяционных полиномов будет разрывной их первая производная, поэтому для решения задачи кусочно-линейной интерполяции используют особый вид кусочно-полиномиальной интерполяции — сплайн-интерполяцию. Сплайн — это функция, которая на каждом частичном отрезке интерполяции является алгебраическим многочленом, а на всем заданном отрезке непрерывна вместе с несколькими своими производными.
|
|
|
Математически сплайны моделируют старое механическое устройство из гибких реек. Если их жестко закрепить в узлах интерполяции, то рейки принимают форму, минимизирующую их потенциальную энергию
Основные характеристики сплайнов:
- количество и расположение узлов;
- наибольший порядок m многочлена, из которого склеен сплайн;
- гладкость сплайна в узлах.
Пусть на отрезке 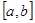 задана функция аналитически (в виде
задана функция аналитически (в виде  ), таблично или графически. Для замены этой функции сплайном разобьем отрезок
), таблично или графически. Для замены этой функции сплайном разобьем отрезок 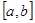 на n частей и составим таблицу:
на n частей и составим таблицу:
Функция 
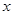
| 
| 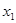
| 
| 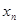
|

| 
| 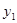
| 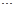
| 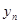
|
Здесь  ,
, 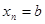 , а
, а  - значения функции
- значения функции 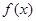 при
при 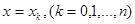 .
.
Дадим математическое определение сплайна. Сплайном степени m называется функция  удовлетворяющая следующим свойствам:
удовлетворяющая следующим свойствам:
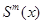 непрерывна на
непрерывна на 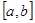 вместе со всеми производными до некоторого порядка р;
вместе со всеми производными до некоторого порядка р;
На каждом отрезке 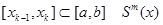 совпадает с некоторым многочленом Pm,k(x) степени m
совпадает с некоторым многочленом Pm,k(x) степени m
Пусть в каждой точке  существует непрерывная производная
существует непрерывная производная 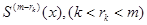 . А следующая производная
. А следующая производная  может быть уже разрывная. Дефектом в сплайне называется число
может быть уже разрывная. Дефектом в сплайне называется число 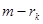 в точке
в точке  . Если мы возьмем
. Если мы возьмем 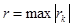 , то это тоже дефект сплайна.
, то это тоже дефект сплайна.
Интерполяция ломаными это самый простой сплайн первой степени с дефектом, равным единице. В этом случае сама функция непрерывна, а уже первая производная разрывная. Если функция задана таблично, то значения 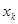 выбираем из таблицы; при этом, чем больше n, тем лучше аппроксимация. На каждом из элементарных отрезков
выбираем из таблицы; при этом, чем больше n, тем лучше аппроксимация. На каждом из элементарных отрезков  заменяем функцию
заменяем функцию  отрезком прямой:
отрезком прямой: 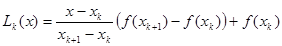 .
.
|
|
|
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 1223; Нарушение авторских прав?; Мы поможем в написании вашей работы!