
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Бесконечно малые и бесконечно большие функции. 5 страница
|
|
|
|
а) 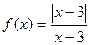 ;
;
б) 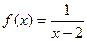 ;
;
в) 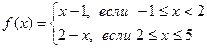 .
.
18.6. Доказать, что уравнение 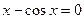 имеет на отрезке
имеет на отрезке 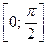 хотя бы один корень.
хотя бы один корень.
18.7. Принимает ли функция 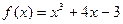 значение 11 на отрезке
значение 11 на отрезке 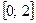 .
.
18.8. Проверить, имеет ли уравнение 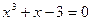 действительные корни на отрезке
действительные корни на отрезке 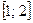 .
.
Задания для самостоятельной работы
18.9. Доказать, что функция  ,
, 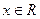 , непрерывна в любой точке
, непрерывна в любой точке 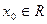 .
.
18.10. Исследовать непрерывность функции 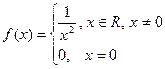 , в точке
, в точке 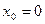 .
.
18.11. Доказать, пользуясь свойствами функций, непрерывных в точке, что функция 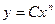 (С – постоянная),
(С – постоянная), 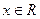 ,
, 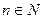 , непрерывна на всей числовой прямой.
, непрерывна на всей числовой прямой.
18.12. Доказать, что любой рациональная функция непрерывна в любой точке своей области определения.
18.13. Исследовать заданные функции на непрерывность и выяснить характер их точек разрыва, сделать чертеж:
а) 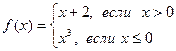 ; б)
; б) 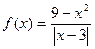 ;
;
в) 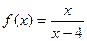 .
.
18.14. Проверить, имеет ли заданное уравнение действительные корни на указанном отрезке.
1) 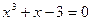 ,
, 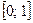 ;
;
2) 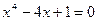 ,
,  ;
;
3) 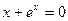 ,
,  .
.
Практическое занятие № 19 (2 часа).
Тема: Производная функции.
План:
1. Понятие производной.
2. Таблица производных. Правила дифференцирования.
3. Производная сложной функции.
4. Производная обратной функции.
5. Производная параметрически заданной функции.
6. Производная неявно заданной функции.
7. Производные высших порядков.
Методические рекомендации к занятию. Студенты должны знать две классические задачи, которые приводят к понятию производной: задачу об уравнении касательной к кривой и задачу о скорости неравномерного прямолинейного движения. Их решение выявляет геометрический и механический смысл производной. Нужно четко знать определение производной, представлять её физический смысл, уметь составить уравнение касательной к графику любой функции 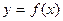 в заданной точке.
в заданной точке.
Изучая материал этой темы, студенты знакомятся с необходимым условием дифференцируемости функции. Необходимо четко уяснить, что из дифференцируемости функции в некоторой точке следует её непрерывность в этой точке. Обратная теорема не справедлива, так как существуют непрерывные функции, которые в некоторых точках могут не иметь производной.
|
|
|
Студентам необходимо усвоить основные правила дифференцирования, уметь находить производную суммы и произведения нескольких дифференцируемых функций, производную частного двух функций, пользоваться основными формулами дифференцирования.
Наиболее важным для овладения техникой дифференцирования функций, и к тому же наиболее трудным, является правило дифференцирования сложной функции. Знание этого правила способствует успешному освоению техники дифференцирования функций.
Необходимо также знать формулу для нахождения производной параметрически заданной функции, уметь находить производную неявно заданной функции и производные высших порядков.
Контрольные вопросы
1. Какие задачи приводят к понятию производной?
2. Что называется производной функции в точке?
3. Какая функция называется дифференцируемой?
4. В чём состоит геометрический смысл производной?
5. В чём состоит физический смысл производной?
6. Сформулируйте необходимое условие существования производной. Является ли это условие достаточным?
7. Приведите примеры функций, которые не имеют производной в некоторой точке.
8. Как находится производная суммы, разности, произведения и частного двух функций?
9. Сформулируйте теорему о производной сложной функции.
10. Сформулируйте теорему о производной обратной функции.
11. По какой формуле находится производная функции, заданной параметрически?
12. Что называется второй производной (производной второго порядка) данной функции?
13. Что называется n-ой производной (производной n-го порядка) данной функции?
|
|
|
14. В чём состоит физический смысл второй производной?
Практические задания, выполняемые на занятии
19.1. Используя определение производной, найти производные функций в точке 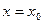 :
:
а) 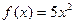 ; б)
; б) 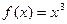 ; в)
; в) 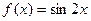 .
.
19.2. Найти производные функции, используя правила дифференцирования и таблицу производных
1) 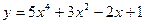 ; 2)
; 2)  ;
;
3) 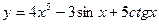 ; 4)
; 4) 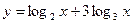 ;
;
5) 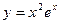 ; 6)
; 6) 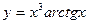 ;
;
7) 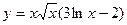 ; 8)
; 8) 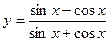 .
.
19.3. Найти производную сложной функции
1) 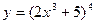 ; 2)
; 2) 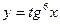 ;
;
3) 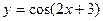 ; 4)
; 4) 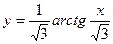 ;
;
5) 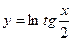 ; 6)
; 6) 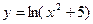 ;
;
7) 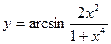 ,
, 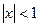 ; 8)
; 8) 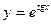 ;
;
9) 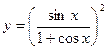 ; 10)
; 10) 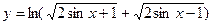 .
.
19.4.* Найти производные степенно-показательных функций:
1) 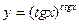 ; 2)
; 2) 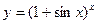 ; 3)
; 3) 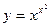 .
.
19.5. Найти производную параметрически заданной функции:
а) 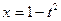 ,
, 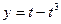 ; б)
; б) 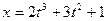 ,
, 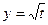 ; в)
; в) 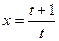 ,
, 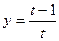 .
.
19.6. Найти производную 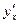 неявно заданной функции:
неявно заданной функции:
а) 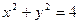 ; б)
; б) 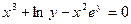 ; в)
; в) 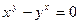 .
.
19.8. Найти производные второго порядка для следующих функций:
а) 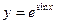 ; б)
; б) 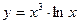 ; в)
; в) 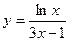 ; г)
; г) 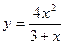 ; д)
; д) 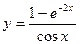 .
.
19.9. Найти 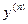 .
.
а) 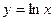 ; б)
; б) 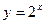 ; в)
; в) 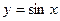 .
.
19.10. Точка движется прямолинейно по закону 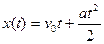 . Найти мгновенную скорость этой точки: 1) при
. Найти мгновенную скорость этой точки: 1) при 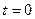 ; 2) в момент
; 2) в момент 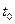 .
.
19.11. Висящий мост имеет форму дуги параболы 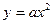 . Пролет моста
. Пролет моста 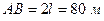 , стрела пролета
, стрела пролета 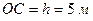 . Определить угол провисания
. Определить угол провисания 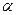 в точке А.
в точке А.
19.12. Массу (в граммах) куска стержня АВ длиной 10 см определяют по формуле 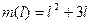 , где
, где 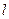 – расстояние от точки А до конца куска В. Определить линейную плотность стержня на его конце В.
– расстояние от точки А до конца куска В. Определить линейную плотность стержня на его конце В.
Задания для самостоятельной работы
19.13. Используя определение производной, найти производные функций в точке 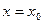 :
:
а) 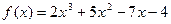 ; б)
; б) 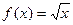 ; в)
; в) 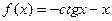 .
.
19.14. Найти производные функции, используя правила дифференцирования и таблицу производных
1) 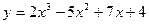 ; 2)
; 2) 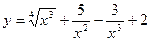 ;
;
3) 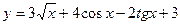 ; 4)
; 4) 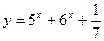 ;
;
5) 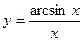 ; 6)
; 6) 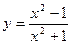 ;
;
7) 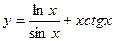 ; 8)
; 8) 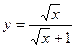 .
.
19.15. Найти производную сложной функции
1) 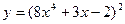 ; 2)
; 2) 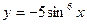 ;
;
3) 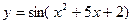 ; 4)
; 4) 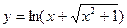 ;
;
5) 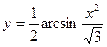 ; 6)
; 6) 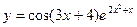 ;
;
7) 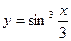 ; 8)
; 8) 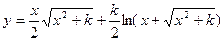 ;
;
9) 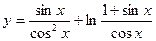 ; 10)
; 10) 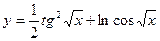 .
.
19.16.* Найти производные степенно-показательных функций:
1) 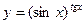 ; 2)
; 2) 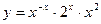 ; 3)
; 3) 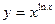 .
.
19.17. Найти производную параметрически заданной функции:
а) 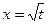 ,
,  ; б)
; б) 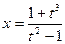 ,
, 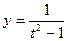 ; в)
; в) 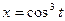 ,
, 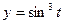 .
.
19.18. Найти производную 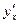 неявно заданной функции:
неявно заданной функции:
а) 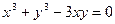 ; б)
; б) 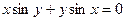 ;
;
в) 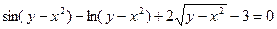 .
.
19.19. Найти производные второго порядка для следующих функций:
а) 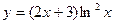 ; б)
; б) 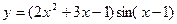 ; в)
; в) 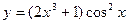 ; г)
; г)  ;
;
д) 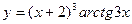 .
.
19.20. Найти 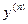 .
.
а) 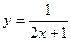 ; б)
; б) 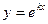 ; в)
; в) 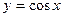 .
.
19.21. Точка движется прямолинейно по закону 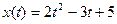 . Найти мгновенную скорость этой точки: 1) при
. Найти мгновенную скорость этой точки: 1) при 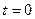 ; 2) в момент
; 2) в момент 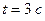 .
.
19.22. Стороны 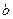 и
и 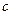 прямоугольника изменяются по закону
прямоугольника изменяются по закону 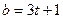 ,
, 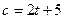 . С какой скоростью изменяется его площадь и периметр в момент времени
. С какой скоростью изменяется его площадь и периметр в момент времени 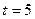 .
.
19.23. Закон радиоактивного распада выражается формулой 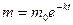 , где
, где 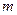 – масса радиоактивного вещества, которое не распалось,
– масса радиоактивного вещества, которое не распалось, 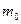 – начальная масса вещества,
– начальная масса вещества, 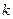 – постоянная распада,
– постоянная распада, 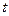 – время распада. Определить скорость радиоактивного распада в начальный момент времени.
– время распада. Определить скорость радиоактивного распада в начальный момент времени.
|
|
|
Практическое занятие № 20 (2 часа).
Тема: Дифференциал функции. Формула Тейлора.
План:
1. Определение дифференциала функции.
2. Использование дифференциала в приближенных вычислениях.
3. Дифференциалы высших порядков.
4. Формула Тейлора с остаточным членом в форме Лагранжа.
5. Формулы Тейлора для некоторых элементарных функций.
Методические рекомендации к занятию. Дифференциал функции – главная линейная относительно приращения аргумента часть приращения функции.
Так как дифференциал функции равен произведению её производной на дифференциал аргумента, то операция нахождения дифференциала сводится к нахождению производной и также называется дифференцирование функции.
Контрольные вопросы
1. Что называется дифференциалом функции?
2. Пусть 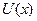 и
и 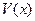 – дифференцируемые функции. Запишите равенства для дифференциала суммы, разности, произведения и частного этих функций.
– дифференцируемые функции. Запишите равенства для дифференциала суммы, разности, произведения и частного этих функций.
3. В чём состоит свойство инвариантности формы дифференциала относительно выбора переменных?
4. В чём заключается геометрический смысл дифференциала функции?
5. Какая формула является основной для простейших приближенных вычислений с помощью дифференциала?
6. Запишите формулу Тейлора с остаточным членом в форме Лагранжа.
7. Какой многочлен называется многочленом Тейлора?
8. Какая формула называется формулой Маклорена?
9. Запишите формулу Тейлора для функций 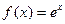 ,
, 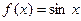 ,
, 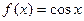 в точке
в точке 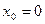 .
.
10. Запишите формулу Тейлора для функций 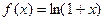 ,
, 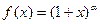 в точке
в точке 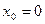 .
.
Практические задания, выполняемые на занятии
20.1. Найти дифференциалы следующих функций:
1) 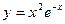 ; 2)
; 2) 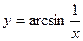 ; 3)
; 3) 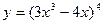 ; 4)
; 4) 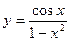 ; 5)
; 5) 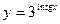 ;
;
6) 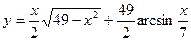 ; 7)
; 7) 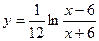 .
.
20.2. Найти дифференциалы первого, второго и третьего порядков функций:
а) 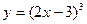 ; б)
; б) 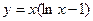 .
.
20.3. Сравнить приращение и дифференциал функции 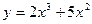 .
.
20.4. Вычислить приближенное значение:
а) 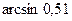 ; б)
; б) 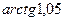 ; в)
; в) 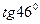 ; г)
; г) 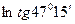 ; д)
; д) 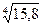 .
.
20.5. Вычислить приближенное значение площади круга, радиус которого равен 3,02 м.
20.6. Разложить функцию 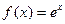 в ряд Тейлора по степеням
в ряд Тейлора по степеням 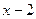 .
.
20.7. Разложить функцию 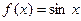 в ряд Тейлора по степеням
в ряд Тейлора по степеням 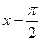 .
.
20.8. Разложить в ряд Тейлора по степеням 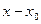 функцию
функцию 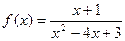 , если:
, если:
а) 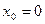 ; б)
; б) 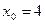 .
.
20.9. Какую погрешность имеет приближение 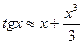 на отрезке
на отрезке 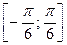 ?
?
|
|
|
20.10. Вычислить с точность до 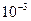 приближенное значение
приближенное значение 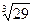 .
.
Задания для самостоятельной работы
20.11. Найти дифференциалы следующих функций:
1) 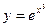 ; 2)
; 2) 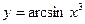 ; 3)
; 3) 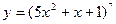 ; 4)
; 4) 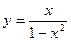 ; 5)
; 5) 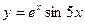 ;
;
6) 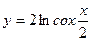 ; 7)
; 7) 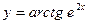 .
.
20.12. Найти дифференциала первого и второго порядков функций:
а) 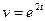 ; б)
; б) 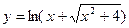 .
.
20.13. Найти дифференциал и приращение функции 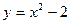 при
при 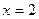 и
и 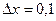 . Вычислить абсолютную и относительную погрешности, которые получаются при замене приращения функции её дифференциалом.
. Вычислить абсолютную и относительную погрешности, которые получаются при замене приращения функции её дифференциалом.
20.14. Вычислить приближенное значение:
а)  ; б)
; б) 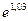 ; в)
; в) 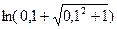 ; г)
; г) 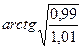 ; д)
; д) 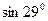 .
.
20.15. Найти приближенное значение объема шара радиуса 2,01 м.
20.16. Разложить функцию 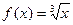 в ряд Тейлора по степеням
в ряд Тейлора по степеням 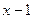 .
.
20.17. Разложить функцию 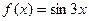 в ряд Тейлора по степеням
в ряд Тейлора по степеням 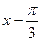 .
.
20.18. Разложить в ряд Тейлора в окрестности точки 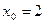 функцию
функцию 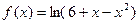 .
.
20.19. Какую погрешность имеет приближение 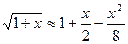 на отрезке
на отрезке 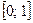 ?
?
20.20. Вычислить с точность до 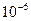 приближенное значение
приближенное значение 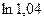 .
.
Практическое занятие № 21 (2 часа).
Тема: Приложения производной функции. Построение графика функции.
План:
1. Правило Лопиталя.
2. Уравнения касательной и нормали к кривой.
3. Интервалы монотонности.
4. Экстремумы функции.
5. Выпуклость графика функции.
6. Схема исследования функции и построения её графика.
7. Отыскание наибольшего и наименьшего значений функции.
Методические рекомендации к занятию. Одно из простейших приложений производной – раскрытие неопределенностей вида 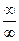 и
и 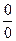 – правило Лопиталя. Следует обратить внимание на то, что согласно этому правилу предел отношения двух бесконечно малых или двух бесконечно больших функций равен пределу отношения их производных, а не пределу производной частного этих функций.
– правило Лопиталя. Следует обратить внимание на то, что согласно этому правилу предел отношения двух бесконечно малых или двух бесконечно больших функций равен пределу отношения их производных, а не пределу производной частного этих функций.
Теоремы дифференциального исчисления являются обоснование такой важной области приложений производных, как исследование функций. Студенты должны знать эти теоремы, четко различать в них условие и заключение и уметь применять их при исследовании функции.
Большая серия задач на приложения производной – это исследование функции и построение её графика. Студентам необходимо знать схему исследования функции и уметь строить графики.
Контрольные вопросы
1. Как с помощью правила Лопиталя раскрывать неопределенности вида 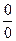 и
и 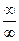 при
при 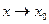 (или при
(или при 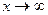 )?
)?
2. Какие другие виды неопределенностей вы знаете? Как раскрываются эти неопределенности?
3. Какой вид имеет уравнение касательной к кривой?
4. Что называется нормалью к кривой?
5. Какой вид имеет уравнение нормали к кривой?
6. Какие интервалы называются интервалами монотонности функции?
7. В чем состоит необходимое условие возрастанию (убывания) функции на интервале?
8. Сформулируйте теорему Ролля.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 462; Нарушение авторских прав?; Мы поможем в написании вашей работы!