Разложение периодических функций в ряд Фурье

Известно, что периодические функции , удовлетворяющие некоторым условиям, могут быть представлены в виде линейной комбинации (суммы с весовыми коэффициентами) ортогональных функций:

(7.1)

Ортогональной на отрезке [a, b] называется система функций

,

удовлетворяющая условию

При разложении периодических функций в ряд Фурье в качестве ортогональных берут гармонические функции

Для представления в виде ряда Фурье периодическая функция 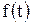должна удовлетворять условиям Дирихле: в пределах периода Т функция имеет конечное число разрывов, максимумов и минимумов. Реальные ЭДС, токи и напряжения в электрических цепях удовлетворяют этим условиям. Таким образом, несинусоидальная периодическая функция может быть представлена в виде бесконечного гармонического ряда Фурье:

, (7.2)

где А₀ – постоянная составляющая, А_n – амплитуда n-й гармоники, j_n – начальная фаза n-й гармоники, nw₁ – частота n-й гармоники. Частота 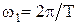называется основной частотой. В ряде Фурье каждая гармоническая составляющая имеет свои амплитуду, частоту и начальную фазу. Используя тригонометрические преобразования, ряд Фурье можно представить в виде

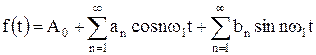, (7.3)

где коэффициенты ряда Фурье вычисляются по формулам, полученным на основе свойства ортогональности гармонических функций:

(7.4)

Между коэффициентами ряда Фурье в форме (7.2) и (7.3) существует связь:

.

Для четных функций b_n=0, для нечетных функций a_n=0.

Набор коэффициентов ряда Фурье А_n и j_n образует спектры амплитуд и фаз периодической несинусоидальной функции. Амплитудный спектр принято изображать в виде диаграммы (рис. 7.2).

Спектр периодических функций линейчатый. Расстояние между соседними линиями равно основной частоте .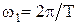

Дата добавления: 2014-12-26