Магнитостатика

Магнитное поле постоянного тока

Для случая постоянного тока система уравнений электромагнитного поля имеет следующий вид.

Уравнения электростатики:

1). ();

2). ();

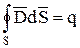3). .

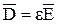Уравнения, характеризующие магнитное поле:

1). ;

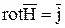
2). ;

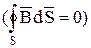3). .

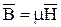Рассматривает лишь области, не содержащие тока (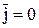). В этом случае верхняя строчка системы уравнений магнитного поля будет иметь вид:

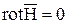
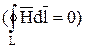. (10.45)

Тогда из уравнения (10.45) следует: в областях, где 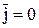, магнитное поле можно рассматривать как потенциальное (по аналогии сэлектростатическим), то есть как поле, каждая точка которого имеет скалярный магнитный потенциал j_м. Тогда

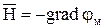. (10.46)

Так как

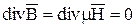, (10.47)

то при m=const получим

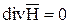. (10.48)

Заменив на , получим

. (10.49)

Таким образом, скалярный потенциал магнитного поля подчиняется уравнению Лапласа:

. (10.50)

Кроме того, граничные условия для вектора 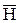(10.5), (10.13) точно такие же, как и для вектора 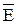(10.8), (10.19). Отсюда очевидный вывод: решения задач магнитостатики формально аналогичны решениям соответствующих задач электростатики и могут быть получены простой заменой на 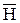и e на m. На самом деле на практике не каждой электростатической задаче можно сопоставить магнитостатическую. Явлений магнитостатики гораздо меньше в природе, так как не существует свободных магнитных зарядов.

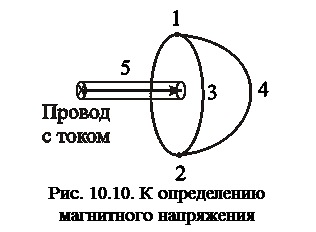
Разность скалярных магнитных потенциалов между точками 1 и 2 (рис. 10.10) называют падением магнитного напряжения между этими точками.

Падение магнитного напряжения между точками 1 и 2 по какому-либо одному пути (например, по пути 1-3-2) равно падению магнитного напряжения между теми же точками по какому-либо другому пути (например, 1-4-2) в том случае, когда эти пути образуют замкнутый контур, ток внутри которого равен нулю.

Если же замкнутый контур, образованный двумя путями, охватывает некоторый не равный нулю ток, то падение магнитного напряжения по первому пути не равно падению магнитного напряжения по второму пути: они будут различаться на величину тока, охваченного контуром. (Это вытекает из закона полного тока.)

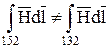, (10.51)

так как из закона полного тока следует, что .

Таким образом, с помощью скалярного потенциала нельзя решить задачу о связи магнитного поля и постоянного тока. С этой целью вводится векторный потенциал ( или вектор-потенциал) магнитного поля. Это – некая вспомогательная функция (обозначим её ), плавно изменяющаяся от точки к точке; её ротор равен магнитной индукции:

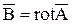. (10.52)

Определим так, чтобы уравнения магнитного поля 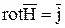(1); (2) 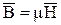(3) выполнялись во всем пространстве: и там, где токов нет, и там, где есть токи ().

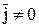Уравнение (2) выполняется, так как 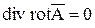. Рассмотрим оставшиеся два уравнения.

Ограничимся рассматриванием однородной среды m=const. Умножим правую и левую части уравнения (1) на m:

, (10.53)

а так как то .

Операция взятия ротора от ротора – это операция раскрытия двойного векторного произведения, выполняется так:

.

Из курса математики известно, что двойное векторное произведение раскрывается следующим образом:

.

В нашем случае роль векторов 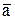и 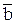играет оператор Ñ, а роль вектора 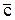– вектор-потенциал , то есть:

.

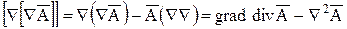До сих пор никаких дополнительных требований к векторному потенциалу не предъявлялось, кроме того, что он должен быть функцией, имеющей пространственные производные. Так как есть расчетная функция, то в магнитном поле постоянного тока ее можно подчинить требованию

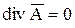, (10.54)

то есть поле вектора не имеет источников. Тогда

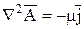. (10.55)

Это уравнение аналогично уравнению Пуассона для электростатического потенциала и может быть записано в виде трёх скалярных:

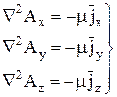. (10.56)

Решение этих уравнений можно записать аналогично решению уравнения Пуассона для электростатического потенциала (заменив U на A_x и mj_xна r/e):

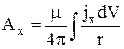, (10.57)

так же и для других составляющих (A_y и A_z). Тогда векторная запись решения уравнения Пуассона для векторного потенциала будет выглядеть так:

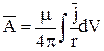, (10.58)

где r– расстояние от центра элемента объема dV, в котором существует ток 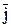, до точки, в которой определяется .

Полученное выражение справедливо везде, в том числе и там, где токи отсутствуют (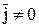). Полученный результат позволяет по заданному току найти векторный потенциал и затем по нему определить поле, то есть индукцию 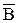и напряженность .

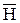Дата добавления: 2014-12-26