
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методы криптоанализа симметричных криптосистем 1 страница
|
|
|
|
По определению известного американского криптолога У. Фридмана «криптоанализ включает определение используемого языка, типа криптосистемы, ключа и исходного текста; обычно именно в этом порядке». Хотя определение криптоанализа было введено сравнительно недавно, первым известным письменным упоминанием о криптоанализе является «Книга о большом стремлении человека разгадать загадки древней письменности», написанная арабским учёным Абу Вакр бен Али бен Вахшия ал-Набати в средние века. В настоящее время криптоанализ активно развивается, хотя единая математическая теория криптоанализа еще не разработана, и на рынке уже появились пакеты прикладных программ по криптоанализу. В частности, разработкой таких программных продуктов занимается американская фирма Access Data Recovery.
3.1. Задачи и принципы криптоанализа
Следует заметить сразу, что основная цель криптоанализа состоит не столько в получении скрываемой информации, а в оценке стойкости существующих и разрабатываемых криптосистем. Оценка стойкости криптосистем представляется в виде количества операций, необходимых для взлома криптосистемы или в виде времени, которое требуется для взлома.
Приведем основные принципы, которые были «выстраданы» криптологами [5,10]:
1. Принцип Керкхоффа. Только криптоаналитик может судить о криптостойкости системы.
2. Принцип Керкхоффа-Шеннона. Противник знает используемую криптосистему с точностью до ключевой информации.
3. Принцип Жеверже. Поверхностные усложнения криптосистемы могут быть иллюзорны, так как порождают ложные оценки ее криптостойкости.
4. При оценке криптостойкости необходимо учитывать возможные криптографические ошибки и другие нарушения дисциплины безопасности.
|
|
|
Из приведенных выше принципов следует, что основная задача криптоаналитика заключается в оценке ключевой информации, при условии, что сама используемая криптосистема известна. Алгоритм оценки ключевой информации называется криптоатакой. В зависимости от условий взаимодействия криптоаналитика с криптосистемой различают следующие основные типы криптоатак:
- криптоатака с использованием только криптограмм (А1);
- криптоатака с использованием открытых текстов и соответствующих им криптограмм (А2);
- криптоатака с использованием выбираемых криптоаналитиком открытых текстов и соответствующих им криптограмм (А3);
- криптоатака с использованием аппаратного воздействия на криптосистему (криптоатака по сторонним каналом) (А4).
Последний тип криптоатак А4 предполагает не исследования теоретического описания криптографического алгоритма, а анализ данных, полученных в результате наблюдения за физическим процессом работы устройства, реализующего криптографический алгоритм. К этому типу криптоатак относятся: криптоатака по времени, криптоатака по энергопотреблению, криптоатака по электромагнитному излучению, криптоатака на основе акустического анализа.
В настоящее время разработано множество методов криптоанализа, реализующих криптоатаки типов А1-А3. В настоящей главе рассмотрим несколько этих типов криптоатак.
3.2. Метод полного перебора
Метод полного перебора или метод «грубой силы» (brute force attack) является простейшим методом криптоанализа, и несмотря на свой «солидный возраст» в настоящее время, в связи с интенсивных развитием компьютерной техники, находит достаточно широкое применение. Суть метода заключается в следующем:
1) на основе имеющейся криптограммы  и соответствующего ей открытого текста
и соответствующего ей открытого текста  составляется система уравнений относительно
составляется система уравнений относительно 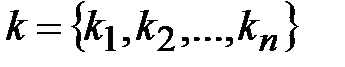 :
:
|
|
|
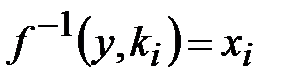 ,
, 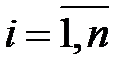 , (3.1)
, (3.1)
полным перебором всех возможных значений ключевого параметра находится некоторое множество решений  ;
;
2) если количество найденных решений  , то считается что истинное значение ключевого параметра определено, если
, то считается что истинное значение ключевого параметра определено, если 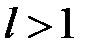 (несколько осмысленных открытых текстов), то определено подмножество значений искомого ключевого параметра и в этом случае целесообразно увеличить количество уравнений в системе.
(несколько осмысленных открытых текстов), то определено подмножество значений искомого ключевого параметра и в этом случае целесообразно увеличить количество уравнений в системе.
Если считать проверку одного варианта ключа 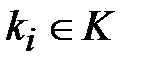 в выражении (3.1) за одну операцию, то полный перебор ключей потребует
в выражении (3.1) за одну операцию, то полный перебор ключей потребует  операций. Пусть ключ в алгоритме шифрования выбирается случайно и равновероятно из множества
операций. Пусть ключ в алгоритме шифрования выбирается случайно и равновероятно из множества  . Тогда с вероятностью
. Тогда с вероятностью  трудоемкость метода полного перебора равна 1. Это происходит в том случае, когда случайно выбран ключ, расположенный в нашем порядке на первом месте. Поэтому естественно в качестве оценки трудоемкости метода взять математическое ожидание числа шагов в переборе до попадания на использованный ключ. Пусть случайная величина
трудоемкость метода полного перебора равна 1. Это происходит в том случае, когда случайно выбран ключ, расположенный в нашем порядке на первом месте. Поэтому естественно в качестве оценки трудоемкости метода взять математическое ожидание числа шагов в переборе до попадания на использованный ключ. Пусть случайная величина  - число опробований включительно до момента обнаружения использованного ключа. При
- число опробований включительно до момента обнаружения использованного ключа. При 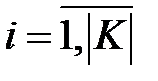 случайные величины
случайные величины  1, если использованный ключ находиться в порядке на месте
1, если использованный ключ находиться в порядке на месте  и
и  0 в противном случае. Тогда:
0 в противном случае. Тогда:
 . (3.2)
. (3.2)
Если считать, что все ключи расположены в установленном порядке, то процедуру равновероятного выбора ключа можно представить как равновероятный выбор числа  в последовательности натуральных чисел
в последовательности натуральных чисел  . Тогда
. Тогда  для любого
для любого 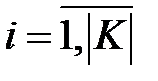 . Подставляя полученное значение в (3.2) имеем:
. Подставляя полученное значение в (3.2) имеем:
 . (3.3)
. (3.3)
При больших  можно приблизительно считать, что
можно приблизительно считать, что 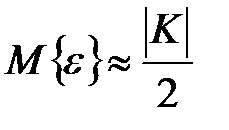 . Например, для криптосистемы DES
. Например, для криптосистемы DES  , тогда средняя трудоемкость полного перебора
, тогда средняя трудоемкость полного перебора  . При использовании современных вычислительных систем, среднее время взлома шифра Цезаря составляет
. При использовании современных вычислительных систем, среднее время взлома шифра Цезаря составляет  секунды, а шифра Вернама -
секунды, а шифра Вернама -  лет.
лет.
Метод полного перебора допускает распараллеливание. Один из способов распараллеливания заключается в том, что множество натуральных чисел  разбивается на непересекающиеся подмножества
разбивается на непересекающиеся подмножества 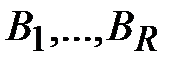 . Система из
. Система из 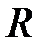 вычислительных машин перебирает ключи так, что
вычислительных машин перебирает ключи так, что  -ая машина осуществляет перебор ключей из множества
-ая машина осуществляет перебор ключей из множества  ,
, 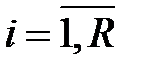 . Система прекращает работу, если одна из вычислительных машин определила ключ. Например, если одна вычислительная машина опробует ключ за
. Система прекращает работу, если одна из вычислительных машин определила ключ. Например, если одна вычислительная машина опробует ключ за  секунд, то для того чтобы найти ключ криптосистемы DES полным перебором за 24 часа требуется
секунд, то для того чтобы найти ключ криптосистемы DES полным перебором за 24 часа требуется 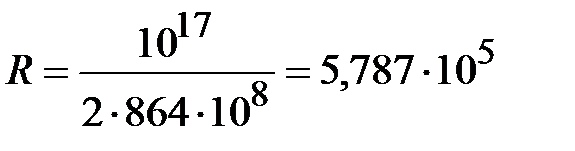 вычислительных машин.
вычислительных машин.
|
|
|
3.3. Методы бесключевого чтения
При рассмотрении поточных криптосистем гаммирования были определены требования к гамме. Нарушение этих требований дает противнику возможность реализовать криптоатаку на криптосистему. Рассмотрим некоторые методы криптоанализа криптосистем гаммирования не требующие определения ключа [11].
Метод чтения в колонках реализует способ восстановления текста, зашифрованного неравновероятной гаммой. Суть метода состоит в следующем. Пусть 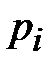 есть вероятность использования знака
есть вероятность использования знака  в гамме, причем полагаем, что не все вероятности
в гамме, причем полагаем, что не все вероятности  равны
равны 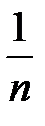 , где
, где 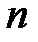 - длина гаммы. Без ущерба для общности положим
- длина гаммы. Без ущерба для общности положим  ,
,  ,
, 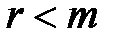 . В
. В 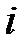 -м такте шифрованию подверглась одна из
-м такте шифрованию подверглась одна из  следующих букв открытого текста,
следующих букв открытого текста, 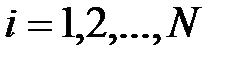 :
:
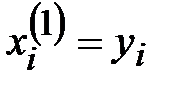 ,
,  , …,
, …,  . (3.4)
. (3.4)
Открытый текст может быть получен подбором 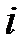 -го знака в
-го знака в  -й колонке табл. 3.1 (элементы таблицы рассматриваются по mod
-й колонке табл. 3.1 (элементы таблицы рассматриваются по mod 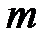 , где
, где  - мощность алфавита).
- мощность алфавита).
Таблица 3.1. Таблица дешифрования
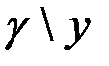
| 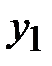
| … | 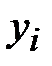
| … | 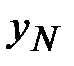
|
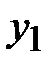
| … | 
| … | 
| |
 -1 -1
| … |  -1 -1
| … | 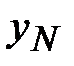 -1 -1
| |
| … | … | … | … | … | … |

| 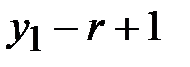
| … | 
| … | 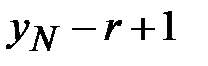
|
Знаки в каждой колонке упорядочены по вероятности их использования в открытом тексте. Это облегчает чтение в колонках, т.к. «читаемый текст» с повышенной вероятностью расположен в верхних строках таблицы. В случае, когда все  >0, но при этом имеют разные значения при составлении таблицы необходимо исключить из рассмотрения
>0, но при этом имеют разные значения при составлении таблицы необходимо исключить из рассмотрения 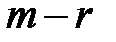 наименее вероятных знаков гаммы. В этом случае существует ненулевая вероятность потери истинного решения, т.е. исходного открытого текста.
наименее вероятных знаков гаммы. В этом случае существует ненулевая вероятность потери истинного решения, т.е. исходного открытого текста.
Применение данного метода тем успешнее, чем меньше высота колонок 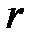 , характеризующая многозначность решения задачи. При
, характеризующая многозначность решения задачи. При 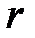 близких к
близких к 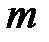 , чтение в колонках теряет смысл, т. к. табл. 3.1 может содержать большое количество осмысленных, но и взаимно противоречивых открытых текстов. Данный метод может быть использован и в случае, когда текст зашифрован периодической гаммой. Пусть дана криптограмма
, чтение в колонках теряет смысл, т. к. табл. 3.1 может содержать большое количество осмысленных, но и взаимно противоречивых открытых текстов. Данный метод может быть использован и в случае, когда текст зашифрован периодической гаммой. Пусть дана криптограмма 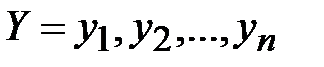 . Известен период ключевой последовательности
. Известен период ключевой последовательности  . Сформируем две подпоследовательности исходной криптограммы:
. Сформируем две подпоследовательности исходной криптограммы:
|
|
|
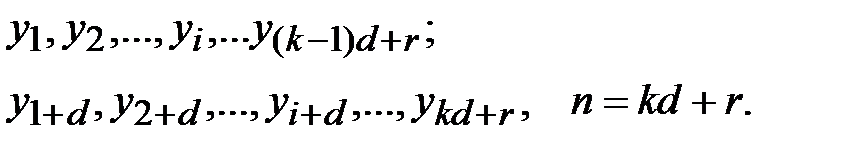
Будем полагать, что открытыми текстами, подлежащими шифрованию, являются содержательные тексты с известными вероятностями букв алфавита 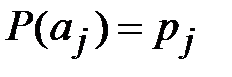 ,
, 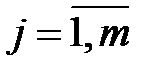 , где
, где  - номер буквы алфавита. Также будем считать, что на множестве
- номер буквы алфавита. Также будем считать, что на множестве 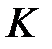 задано равномерное распределение, т.е. ключом является реализация выборки объемом
задано равномерное распределение, т.е. ключом является реализация выборки объемом 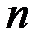 из равномерного распределения
из равномерного распределения  . Тогда вероятность того, что
. Тогда вероятность того, что 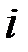 -я и (
-я и (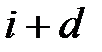 )-я буквы открытого текста были равны соответственно,
)-я буквы открытого текста были равны соответственно, 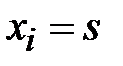 и
и 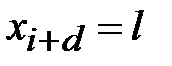 , при условии, что
, при условии, что 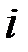 -я и (
-я и ( )-я буквы криптограммы равны соответственно,
)-я буквы криптограммы равны соответственно, 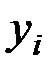 и
и  определяется выражением:
определяется выражением:
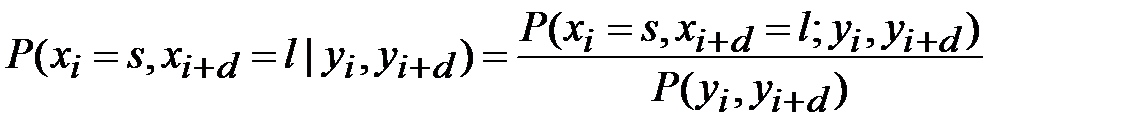 . (3.5)
. (3.5)
Так как в рассматриваемой криптосистеме множество ключей задано латинским квадратом, следовательно, используемый ключ однозначно определен любым переходом в этой замене. Если числитель (3.5) не равен нулю, то справедливо равенство:
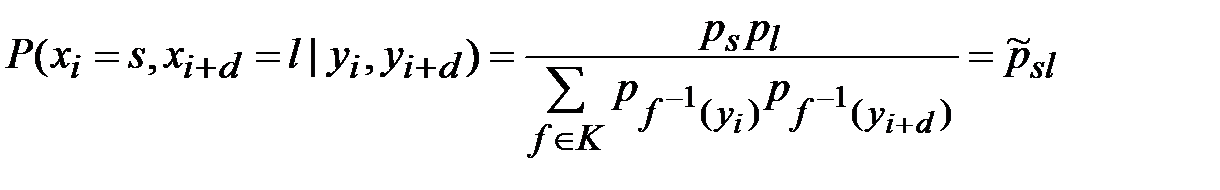 . (3.6)
. (3.6)
Для каждой пары  и
и  букв исходной криптограммы упорядочим в соответствии с убыванием полученных значения условных вероятностей (3.6) пары букв открытого текста
букв исходной криптограммы упорядочим в соответствии с убыванием полученных значения условных вероятностей (3.6) пары букв открытого текста  и
и  .
.
Построив такие колонки для каждого  , в результате получаем таблицу (см. табл. 3.2), в которой верхние пары имеют большую условную вероятность, чем нижние.
, в результате получаем таблицу (см. табл. 3.2), в которой верхние пары имеют большую условную вероятность, чем нижние.
Буквы искомого содержательного текста будут находится вероятнее всего в первых строках и задача сводится к подбору таких пар букв, чтобы в результате получался читаемый текст.
Таблица 3.2. Таблица дешифрования
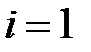
| … | 
| … | 
|
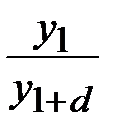
| … | 
| … | 
|
| …. | … | 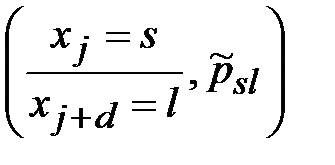
| … | … |
Период ключевой последовательности 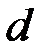 может быть определен с помощью методов Фридмана [1]. Рассмотрим эти методы. Основаны методы на введенном У. Фридманом понятии индекса совпадения. Индексом совпадения последовательности
может быть определен с помощью методов Фридмана [1]. Рассмотрим эти методы. Основаны методы на введенном У. Фридманом понятии индекса совпадения. Индексом совпадения последовательности  называется величина
называется величина
 , (3.7)
, (3.7)
где  ,
,  - некоторая последовательность;
- некоторая последовательность;  - частота встречаемости (число мест в тексте)
- частота встречаемости (число мест в тексте) 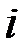 - буквы в последовательности
- буквы в последовательности  .
.
Индекс совпадения  последовательности равен вероятности
последовательности равен вероятности  совпадения символов данной последовательности на случайно и равновероятно выбранных местах
совпадения символов данной последовательности на случайно и равновероятно выбранных местах  и
и 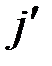 , причем
, причем  и
и  ,
, 
 .
.
При 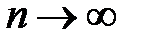
 ,
,
где  - вероятность
- вероятность  го символа из алфавита
го символа из алфавита 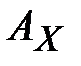 в содержательных текстах.
в содержательных текстах.
При случайном выборе последовательности  индекс совпадения
индекс совпадения  является случайной величиной, и представляет интерес подсчет его математического ожидания. Математическое ожидание индекса совпадения для открытых текстов определяется выражением:
является случайной величиной, и представляет интерес подсчет его математического ожидания. Математическое ожидание индекса совпадения для открытых текстов определяется выражением:
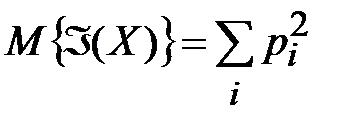 . (3.8)
. (3.8)
Если реализация  представляет собой выборку из равномерного вероятностного распределения, то справедливо выражение:
представляет собой выборку из равномерного вероятностного распределения, то справедливо выражение:
 . (3.9)
. (3.9)
Для любой последовательности 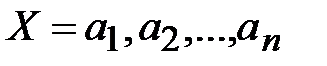 вероятность совпадения
вероятность совпадения  двух случайно и равновероятно выбранных букв последовательности приблизительно равна:
двух случайно и равновероятно выбранных букв последовательности приблизительно равна:
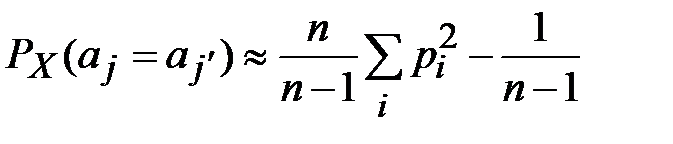 . (3.10)
. (3.10)
Пусть 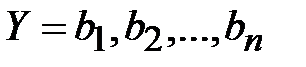 - криптограмма, полученная в результате шифрования случайного текста при случайном и равновероятно выбранном ключе. Тогда математическое ожидание индекса совпадения для криптограммы равно:
- криптограмма, полученная в результате шифрования случайного текста при случайном и равновероятно выбранном ключе. Тогда математическое ожидание индекса совпадения для криптограммы равно:
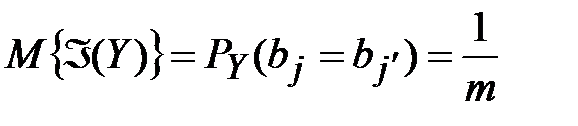 . (3.11)
. (3.11)
Для криптосистемы гаммирования с периодической гаммой, получаемого шифрованием открытого текста  с помощью равновероятного выбора ключа
с помощью равновероятного выбора ключа 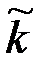 из множества всех локально-периодических последовательностей
из множества всех локально-периодических последовательностей  периода d и
периода d и 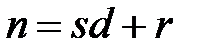 справедливо:
справедливо:
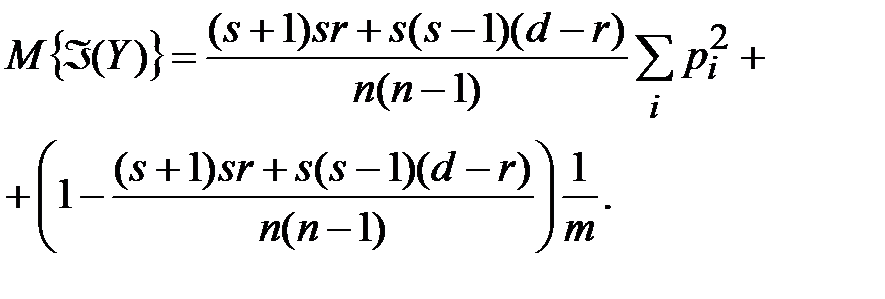 (3.12)
(3.12)
При  (т.е.
(т.е.  ):
):
 (3.13)
(3.13)
Первый метод Фридмана состоит в том, что вычисляется индекс совпадения  для имеющейся криптограммы в соответствии с выражением (3.7) и затем его значение сравнивается с (3.13) при
для имеющейся криптограммы в соответствии с выражением (3.7) и затем его значение сравнивается с (3.13) при 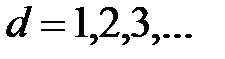 . При достаточной близости индекса совпадения к одному из значений (3.13), при некотором
. При достаточной близости индекса совпадения к одному из значений (3.13), при некотором  , предполагают, что период равен этому значению
, предполагают, что период равен этому значению  .
.
Первый метод Фридмана эффективен для 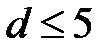 , т.к. значение
, т.к. значение 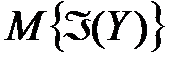 для фиксированного периода
для фиксированного периода  совпадает со значениями целого ряда различных периодов ключевой последовательности.
совпадает со значениями целого ряда различных периодов ключевой последовательности.
Второй метод Фридмана также основан на вычислении индекса совпадения. Суть второго метода Фридмана состоит в опробовании возможных периодов  по следующей схеме. Из исходной криптограммы
по следующей схеме. Из исходной криптограммы  для предполагаемого периода
для предполагаемого периода  ключевой последовательности выписывается
ключевой последовательности выписывается  подпоследовательностей:
подпоследовательностей:
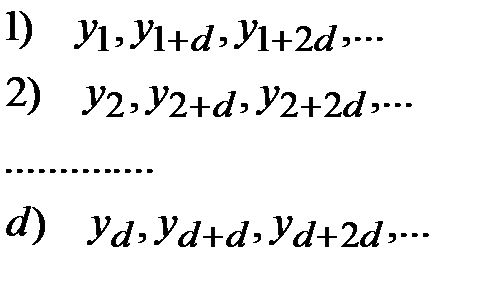 (3.14)
(3.14)
Для каждой подпоследовательности подсчитывается ее индекс совпадения 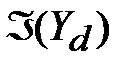 . Если все индексы совпадения в среднем близки к значению
. Если все индексы совпадения в среднем близки к значению  (среднее значение индекса совпадения случайных криптограмм, полученных с помощью гамм периода 1), то принимают величину
(среднее значение индекса совпадения случайных криптограмм, полученных с помощью гамм периода 1), то принимают величину 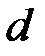 за истинный период, в противном случае опробуется следующая величина периода. Второй метод Фридмана позволяет эффективно определять периоды
за истинный период, в противном случае опробуется следующая величина периода. Второй метод Фридмана позволяет эффективно определять периоды  .
.
Метод восстановления текстов, основанный на атаке с помощью вставки символа (insertion attack). Рассмотрим существо метода. Пусть открытый текст 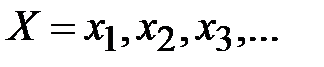 с помощью гаммы
с помощью гаммы  преобразуется в соответствии с уравнением шифрования:
преобразуется в соответствии с уравнением шифрования:
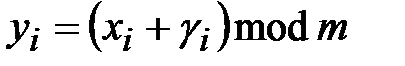 , (3.15)
, (3.15)
в криптограмму  . Криптоаналитику известна криптограмма, но не известен открытый текст и гамма. Предположим, что криптоаналитик располагает еще одной криптограммой, полученной зашифрованием той же гаммой видоизмененного открытого текста, полученного из оригинального текста вставкой в некоторой позиции известного бита
. Криптоаналитику известна криптограмма, но не известен открытый текст и гамма. Предположим, что криптоаналитик располагает еще одной криптограммой, полученной зашифрованием той же гаммой видоизмененного открытого текста, полученного из оригинального текста вставкой в некоторой позиции известного бита 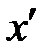 . Пусть видоизмененный открытый текст имеет вид
. Пусть видоизмененный открытый текст имеет вид  , а соответствующая криптограмма
, а соответствующая криптограмма 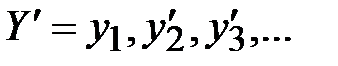
По двум криптограммам, начиная с момента вставки, можно определить и гамму и открытый текст:
 ,
,  ;
;
 ,
, 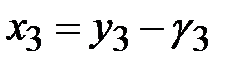 ;
;
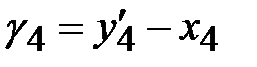 ,
,  , ….
, ….
Все вычисления выполняются по mod 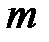 . Момент вставки символа
. Момент вставки символа  можно определить, сравнивая видоизмененную и оригинальную криптограммы. Если значение вставленного символа неизвестны, то можно реализовать подбор вариантов его значения. Для защиты от такого рода атак достаточно никогда не использовать одинаковые отрезки гаммы для повторного шифрования.
можно определить, сравнивая видоизмененную и оригинальную криптограммы. Если значение вставленного символа неизвестны, то можно реализовать подбор вариантов его значения. Для защиты от такого рода атак достаточно никогда не использовать одинаковые отрезки гаммы для повторного шифрования.
3.4. Методы криптоанализа с использованием теории статистических решений
Рассмотрим симметричную криптосистему, криптоаналитику априорно известно:
1) криптографическое преобразование  с точностью до ключа
с точностью до ключа 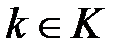 ;
;
2) криптограмма  длинной n.
длинной n.
Задача криптоаналитика состоит в оценке неизвестного параметра  криптографического преобразования
криптографического преобразования  .
.
Допущения (предположения) [10]:
1) исходный текст 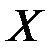 представляет собой случайную последовательность с некоторым заданным дискретным распределением вероятностей
представляет собой случайную последовательность с некоторым заданным дискретным распределением вероятностей 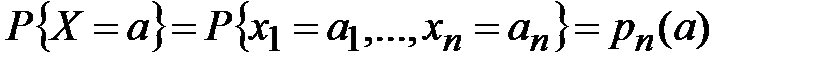 ,
,  ,
, 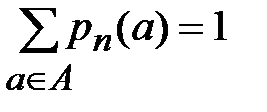 .
.
2) 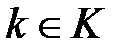 - является детерминированной неизвестной величиной.
- является детерминированной неизвестной величиной.
Метод частотного криптоанализа базируется на реализации методов теории статистических решений, а именно, на методе максимального правдоподобия [10]. В соответствии с этим методом формируется функция правдоподобия:
 , (3.16)
, (3.16)
где 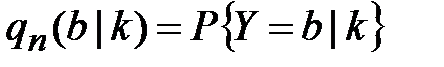 - дискретное распределение крипто граммы Y в ситуации, когда значение ключа
- дискретное распределение крипто граммы Y в ситуации, когда значение ключа  фиксировано:
фиксировано:
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 1966; Нарушение авторских прав?; Мы поможем в написании вашей работы!