Шушляков Д. А. 4 страница

Линия, проведенная через концы отрезков Е (см. рис. 22), называется и в этом случае линией полного напора, но теперь не располагается в горизонтальной плоскости, а понижается в направлении течения; чем больше наклон этой линии, тем интенсивнее расходуется энергия по пути. Отметим, что пьезометрическая линия по-прежнему может, как снижаться, так и повышаться в зависимости от изменения скорости при изменении площади сечения струйки.

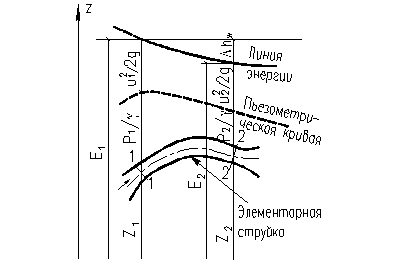
Рис. 22 – К выводу уравнения Бернулли для элементарной струи вязкой

жидкости

Отношение 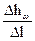потерь напора на длине участка струйки ∆l к самой длине называют средним гидравлическим уклоном для этого участка.

Гидравлический уклон — величина безразмерная и в общем случае переменная. Обычно его обозначают буквой i. Уклон в сечении выражается, очевидно, величиной

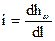(91)

Понятие об уклоне можно ввести и для пьезометрической линии. Средний пьезометрический уклон тогда определится по формуле

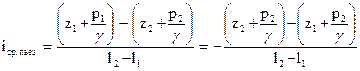. (92)

Пьезометрический уклон может быть положительным, равным нулю и отрицательным.

.

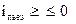Пьезометрический уклон в данном сечении определяется по формуле

.

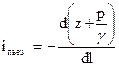4.3. Уравнение неразрывности

Пусть гранями параллелепипеда ABCDA'B'C'D' на рис. 23 ограничивается некоторое неподвижное относительно координатных осей пространство, через которое протекает жидкость.

За время dt через грань ABCD внутрь параллелепипеда втекает масса жидкости ρ udtdydz = δM'_x, а вытекает масса 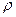'u'dtdydz = δM˝_x.

Плотность 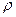и скорость u на входе (в плоскости грани ABCD) в общем случае сжимаемой жидкости не равны плотности 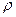' и скорости и' на выходе (в плоскости грани A'B'C'D'). При этом изменения ρ и и обусловливаются только тем, что при переходе от одной грани к другой для сходственных точек этих граней изменяется лишь координата x независимо от времени, так как втекание и вытекание жидкости происходят одновременно. Поэтому:

;

;

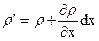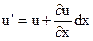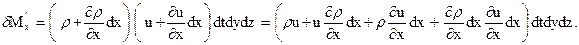
Но

,

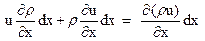последнее слагаемое

-

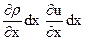бесконечно малая величина высшего порядка относительно других слагаемых, и ею можно пренебречь. Потому

.

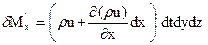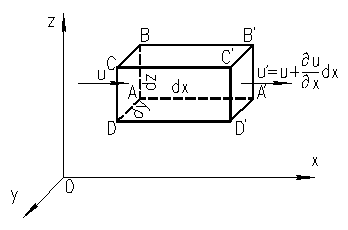
Рис. 23 – К выводу уравнений движения невязкой жидкости

Если за время dtмасса жидкости внутри параллелепипеда увеличилась за счет притока на величину δМ'_Х,а уменьшилась за счет вытекания на величину δМ"_Х,то результативное изменение массы в этом движении вдоль координатной оси 0 х равняется:

.

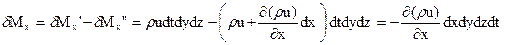Аналогично найдем, что изменения массы в итоге движения вдоль осей 0 у и 0 z равняются соответственно:

;

,

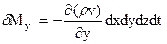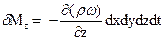а следовательно, общее изменение массы за время dt равно

.

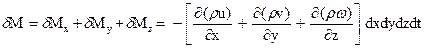Это изменение массы δМ в условиях сплошности потока должно равняться изменению массы, обусловленному изменением плотности.

Плотность ρ есть функция F (х, у, z, t). Определим величину δМ в зависимости от изменения плотности ρ.

В начальный момент t масса внутри параллелепипеда δm'=rdxdydz. По прошествии промежутка времени dt, т. е. в конечный момент t₁ = t+dt, средняя для объема плотность ρ изменится и будет равна r'. Это изменение происходит независимо от координат х, у и z, так как параллелепипед неподвижен, а потому

.

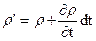Следовательно, в конечный момент t₁ масса жидкости в объеме параллелепипеда

.

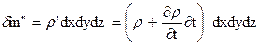Таким образом, приращение массы за время dt будет равно:

.

Так как δМ = δm, то

,

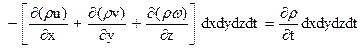что дает после сокращения

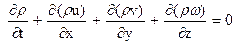. (93)

Это и есть искомое уравнение неразрывности.

В частном случае установившегося движения плотность (как и все остальные параметры движения) от времени не зависит и, следовательно, .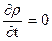

Поэтому уравнение неразрывности получает в этом случае вид

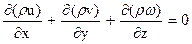. (94)

И, наконец, для несжимаемой жидкости как при установившемся, так и при неустановившемся движении уравнение неразрывности имеет вид

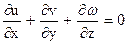. (95)

Отметим здесь, что уравнение неразрывности (95) может быть записано и в другой форме.

Рассмотрим входящие в это уравнение производные, каждая из которых представляет собой частную производную произведения плотности ρ на соответствующие компоненты скорости u, v и w. Так как все эти величины являются функциями координат и времени, то, следовательно:

;

;

.

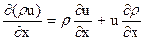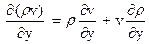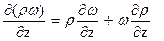Делая подстановку в уравнение (93) и группируя слагаемые, получим

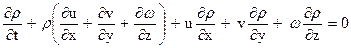. (96)

Но

(если dx, dy и dzрассматриваются как соответствующие проекции элементарного перемещения ds).Тогда, вводя эти обозначения в (96), получим

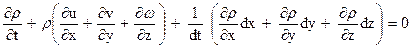
или, умножая на dt,

.

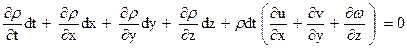Так первые четыре члена представляют собой полный дифференциал функции ρ = F (x, y, z, t), то, деля на ρdt, получим окончательно

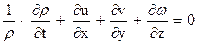. (97)

5. Общие сведения о гидравлических сопротивлениях

5.1. Виды гидравлических сопротивлений

Для определения давлений и средних скоростей в различных сечениях потока выше были выведены два уравнения: уравнение сохранения энергии или полного напора (уравнение Бернулли) и уравнение сохранения массы (уравнение постоянства расхода), которые для несжимаемой жидкости записываются в виде

;

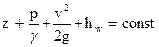vω = Q = const.

Обычно при решении практических задач полный напор Н и расход Q бывают заданы или могут быть определены из известных величин в одном из сечений рассматриваемого потока. Высотное положение центра тяжести сечения z, а также площадь его w, как правило, известны. Таким образом, в этих уравнениях остаются три неизвестных: v, р и h_w.Для их определения необходимо составить третье уравнение, связывающее между собой неизвестные величины, например, уравнение, дающее зависимость h_w от v. С помощью двух уравнений гидравлики удается решать лишь некоторые практические задачи, пренебрегая потерями напора (т. е. принимая h_w=Q).Именно так обстояло дело с рассмотренной выше задачей о трубе Вентури.

Рассмотрим участок трубы, заполненный жидкостью (рис. 24). Если жидкость в трубе не движется, то ее взаимодействие со стенками приводится к одной равнодействующей, направленной вниз (вес жидкости).

При движении жидкости между нею и стенками трубы возникают дополнительные силы сопротивления, в результате чего частицы жидкости, прилегающие к поверхности трубы, тормозятся. Это торможение благодаря вязкости жидкости передается следующим слоям, причем скорость движения частиц по мере удаления их от оси трубы постепенно уменьшается. Равнодействующая сил сопротивления Тнаправлена в сторону, противоположную движению, и параллельна направлению движения (см. рис. 24). Это и есть силы гидравлического трения (сопротивления гидравлического трения).

Для преодоления сопротивления трения и поддержания равномерного поступательного движения жидкости необходимо, чтобы на жидкость действовала сила, направленная в сторону ее движения и равная силе сопротивления, т. е. необходимо затрачивать энергию. Энергию или напор, необходимые для преодоления сил сопротивления, называют потерянной энергией или потерянным напором.

Потери напора, затрачиваемые на преодоление сопротивления трения, носят название потерь напора на трение или потерь напора по длине потока (линейные потери напора) и обозначаются через h_тр.

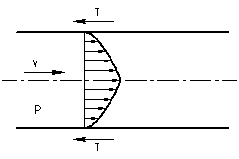
Рис.24 – К понятию о потерях напора на гидравлическое трение

Однако потери напора, возникающие при движении жидкости, зависят не только от трения о стенки. Рассмотрим следующий опыт (рис. 25).

Бак W наполнен водой при постоянном уровне H и питает горизонтальную трубу АВ длиной l одинакового по всей длине диаметра d.Пусть расход воды равен Q. Если трубу АВ заменить трубой CD той же длины l, но образованной из последовательно расположенных участков диаметром соответственно d и 2d, то расход изменится. Пусть новый расход равен Q'. Оказывается, что Q'<Q (иногда Q^/=0,5 Q и даже еще меньше).

Таким образом, трение является не единственной возможной причиной, вызывающей потери напора; резкие изменения сечения также оказывают сопротивление движению жидкости (так называемое сопротивление формы) и вызывают потери энергии. Существуют и другие причины, вызывающие потери напора, например, внезапное изменение направления движения жидкости. Потери напора, вызываемые резким изменением конфигурации границ потока (затрачиваемые на преодоление сопротивления формы), называют местными потерями напора или потерями напора на местные сопротивления и обозначают через h_м.

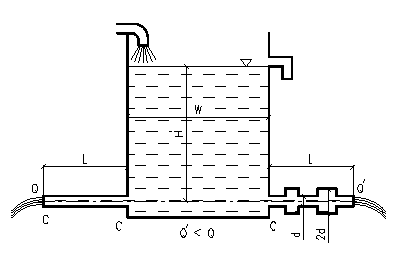
Рис. 25 – К понятию о местных потерях напора

Таким образом, потери напора при движении жидкости складываются из потерь напора на трение и потерь на местные сопротивления, т. е.

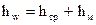. (98)

5.2. Общая формула для потерь напора на трение при равномерном движении жидкости в трубах

Используем метод размерности для определения потерь напора на трение, возникающих при равномерном напорном движении жидкости в трубах.

Опыты показывают, что величина потерь напора на трение hтр при движении жидкости в трубах может зависеть от следующих факторов:

диаметра трубы d и ее длины l;

физических свойств жидкости (плотности ρ и вязкости μ);

средней скорости движения в трубе v;

средней высоты выступов шероховатости kна стенках трубы.

Напишем интересующую нас функциональную зависимость в виде

∆p_тр= f(v, d, μ, ρ, k, l), (99)

где ∆p_тр — потери давления на длине потока, равной l, связанные с потерей напора формулой

∆p_тр = ρgh_тр (100)

Вид функции fв уравнении (99) неизвестен.

Перепишем уравнение (99) в виде

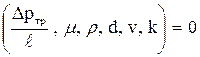f₁ (101)

учитывая, что потеря на трение всегда прямо пропорциональна длине рассматриваемого участка.

Для измерения входящих в формулу (101) n = 6величин требуются m=3основные единицы: масса, время и длина.

Уравнение (101) может быть представлено в форме, содержащей n–m=3безразмерных отношений (чисел ПИ в соответствии с ПИ-теоремой [1, 3, 4]), т. е. вместо (101) можно записать

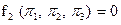, (102)

где 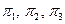- безразмерные комплексы.

Для определения чисел π₁, π₂, π₃выберем из всех переменных три (по числу основных единиц измерения), включающие все основные единицы измерения, например v, d и ρ. Составим теперь уравнения размерностей, объединяющие выбранные переменные с каждой из других переменных по очереди, т. е.:

; (103)

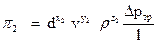; (104)

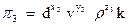. (105)

В выражениях для π₁, π₂, π₃ нужно подобрать показатели при d, vи ρ таким образом, чтобы числа π не имели размерности.

Нетрудно показать (проверив размерности), что

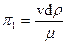; (106)

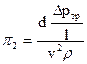; (107)

. (108)

Так, для числа p₃ из условия однородности размерностей

.

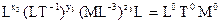Отсюда вытекают следующие уравнения:

при L: x₃ + y₃ - 3z₃+1=0

при T: -y₃ = 0,

при M: z₃ = 0, т.е. x₃ = -1 и π₃ = k/d.

Подставляя (106) - (108) в (102), имеем

.

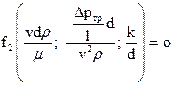Так как нас интересует потеря напора, то разрешаем это уравнение относительно π₂:

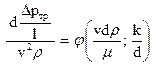
Или

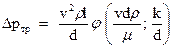. (109)

Учитывая формулу (100), имеем,

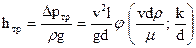
или, обозначая

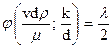. (110)

где λ – безразмерное число, речь о котором будет идти ниже, окончательно получим

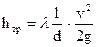. (111)

Из формулы (111) следует, что потеря напора на трение при движении жидкости в трубе возрастает с увеличением средней скорости потока и длины рассматриваемого участка трубы и обратно пропорциональна ее диаметру [6, 7]. Кроме того, в формулу (111) входит неизвестный безразмерный коэффициент λ - так называемый коэффициент гидравлического трения. Эта формула была получена в XIX в. эмпирическим путем и называется формулой Дарси-Вейсбаха.

Приведенный метод можно использовать также для определения вида формулы потерь напора на местные сопротивления. В этом случае, учитывая, что местные потери практически не зависят ни от длины участка трубы, ни от ее диаметра, нетрудно получить формулу

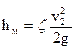, (112)

где ζ - безразмерный коэффициент, так называемый коэффициент местных потерь;

v₂ - скорость потока после прохода через местное сопротивление.

Формулу (112), полученную в XIX в. эмпирическим путем, называют формулой Вейсбаха.

Таким образом, ПИ-теорема, не позволяя получить полного решения вопроса о потерях напора (ибо смысл коэффициентов λ и ζ остался невыясненным), дает возможность ближе подойти к его выяснению. Дальнейшие сведения о коэффициентах λи ζ будут получены после ознакомления с некоторыми особенностями движения жидкости, рассмотрению которых посвящен следующий параграф.

5.3. Ламинарное и турбулентное движение жидкости

Наблюдения показывают, что в природе существуют два различных вида движения жидкости: во-первых, слоистое, упорядоченное или ламинарное движение, при котором отдельные слои жидкости скользят друг относительно друга, не смешиваясь между собой, и, во-вторых, неупорядоченное, так называемое турбулентное движение, когда частицы жидкости движутся по сложным, все время изменяющимся траекториям и в жидкости происходит интенсивное перемешивание.

Рис. 26 – Установка Рейнольдса

Рис. 27 – Режимы движения жидкости

Уже давно было известно, что вязкие жидкости (масла) движутся большей частью упорядоченно, а маловязкие жидкости (вода, воздух) почти всегда неупорядоченно. Ясность в вопрос о том, как именно будет происходить движение жидкости в тех или иных условиях, была внесена в 1883 г. в результате опытов английского физика Рейнольдса.

Опытная установка Рейнольдса представлена на рис. 26. К баку А с водой присоединена стеклянная труба В. Открывая частично вентиль С, можно заставить течь воду по трубе с различными скоростями. Из сосуда D по трубке Е в устье трубы В поступает краска. При малых скоростях движения воды в трубе окрашенная струйка не размывается окружающей ее водой и имеет вид натянутой нити (рис. 27, а). Поток в этом случае называют ламинарным. При увеличении скорости движения воды окрашенные струйки получают вначале волнистое очертание (рис. 27,б), а затем почти внезапно исчезают, размываясь по всему сечению трубы и окрашивая всю жидкость. Движение жидкости становится неупорядоченным, отдельные частицы окрашенной жидкости разлетаются во все стороны, сталкиваются друг с другом, ударяются о стенки и т. д. (рис. 27, в). Такое движение жидкости называют турбулентным. Основная особенность турбулентного движения заключается в наличии поперечных к направлению движения составляющих скорости, накладывающихся на основную скорость в продольном направлении.

Опыты Рейнольдса показали, что переход от ламинарного течения к турбулентному происходит при определенной скорости (так называемая критическая скорость), которая, однако, для труб разных диаметров оказалась различной, возрастающей с увеличением вязкости и уменьшающейся с уменьшением диаметра трубы.

5.4. Число Рейнольдса

Основываясь на некоторых теоретических соображениях [1, 4], а также на результатах опытов, Рейнольдс установил общие условия, при которых возможны существование ламинарного и турбулентного режима движения жидкости и переход от одного режима к другому. Оказалось, что состояние (режим) потока жидкости в трубе зависит от величины безразмерного числа, которое учитывает основные факторы, определяющие это движение: среднюю скорость v, диаметр трубы d, плотность жидкости ρ и ее абсолютную вязкость μ. Это число (позже ему было присвоено название числа Рейнольдса) имеет вид:

.

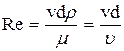Величина d в числе Рейнольдса может быть заменена любым линейным параметром, связанным с условиями течения или обтекания (диаметр трубы, диаметр падающего в жидкости шара, длина обтекаемой жидкостью пластинки и др.)

Значение числа Рейнольдса, при котором происходит переход от ламинарного движения к турбулентному, называют критическим числом Рейнольдса и обозначают Re_кp.

При Re > Re_Kp режим движения является турбулентным, при Re < Re_Kp — ламинарным. Величина критического числа Рейнольдса зависит от условий входа в трубу, шероховатости ее стенок, отсутствия или наличия первоначальных возмущений в жидкости, конвекционных токов и др.

Вопрос о неустойчивости ламинарного движения и его переходе в турбулентное, а также о величине критического числа Рейнольдса подвергся тщательному теоретическому и экспериментальному изучению, но до сих пор не получил еще достаточно полного решения.

Наиболее часто в расчетах принимают для критического числа Рейнольдса значение

Re_кр = 2300, (113)

отвечающее переходу движения жидкости из турбулентного в ламинарное; при переходе движения из ламинарного в турбулентное критическое число Рейнольдса имеет большую величину (для хорошо закругленного плавного входа оно может быть доведено до 20000).

Проведенные исследования показывают также, что критическое значение числа Рейнольдса увеличивается в сужающихся трубах и уменьшается в расширяющихся. Это можно объяснить тем, что при ускорении движения частиц жидкости в сужающихся трубах их тенденция к поперечному перемешиванию уменьшается, а при замедленном течении в расширяющихся трубах усиливается.

По критическому значению числа Рейнольдса легко можно найти также критическую скорость, т. е. скорость, ниже которой всегда будет иметь место ламинарное движение жидкости:

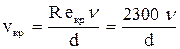. (114)

В трубопроводах систем отопления, вентиляции, газоснабжения, теплоснабжения, водоснабжения и др. движение, как правило, является турбулентным, так как движущаяся среда (вода, воздух, газ, пар) имеет малую вязкость. Так, для газопроводов сети домового потребления числа Рейнольдса бывают обычно не ниже 3000, в городских сетях - не ниже 200 000, в вентиляционных сетях - не ниже 150 000, сетях сжатого воздуха - не ниже 400 000, в паропроводах центрального отопления - не ниже 30 000, а в паропроводах ТЭЦ достигают 3×10⁶ - 5×10⁶. Ламинарный режим для воды и воздуха возможен лишь при их движении в трубах очень малого диаметра. Более вязкие жидкости, например масла, могут двигаться ламинарно даже в трубах значительного диаметра.

Число Рейнольдса имеет большое значение при моделировании гидроаэродинамических явлений.

Числу Рейнольдса можно придать весьма простой смысл. Оно может рассматриваться как мера отношения кинетической энергии рассматриваемого элемента жидкости к работе сил вязкого трения.

Действительно, кинетическая энергия элемента жидкости зависит от его объема и пропорциональна ρv² l ³, где l — линейные размеры элемента жидкости.

Работа сил вязкого трения зависит от размеров поверхности рассматриваемого элемента жидкости и пропорциональна μl ²v.

Отношение кинетической энергии элемента жидкости к работе сил вязкости будет равно:

.

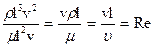Таким образом, число Рейнольдса характеризует относительную роль сил вязкости. Чем меньше число Рейнольдса, тем большую роль играют силы вязкости в движении жидкости. Чем больше число Рейнольдса, тем больше влияние сил инерции в потоке по сравнению с силами вязкости.

5.5. Особенности ламинарного и турбулентного движения жидкости в трубах

Опыты показывают, что одновременно с переходом ламинарного движения в турбулентное изменяется характер распределения скоростей по сечению трубы, а также характер гидравлических сопротивлений. При ламинарном движении распределение скоростей по сечению имеет параболический характер: непосредственно у стенок скорости равны нулю, а при удалении от них непрерывно и плавно возрастают, достигая максимума на оси трубы (рис. 28).

При турбулентном движении закон распределения скоростей сложнее: в пределах большей части поперечного сечения скорости лишь незначительно меньше максимального значения (на оси), но зато вблизи стенок (пограничный слой [5]) величина скорости резко падает (рис. 29).

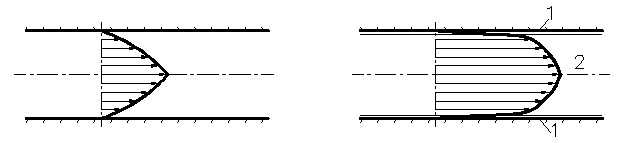
Рис. 28 – Эпюра скоростей при ламинарном движении жидкости в трубопроводе

Рис. 29 – Эпюра скоростей при турбулентном движении жидкости в трубопроводе 1 – пограничный слой; 2 – ядро потока

Более равномерное распределение скоростей по сечению при турбулентном движении объясняется наличием турбулентного перемешивания, осуществляемого поперечными составляющими скоростей. Благодаря этому перемешиванию частицы с большими скоростями в центре потока и с меньшими скоростями на его периферии, непрерывно сталкиваясь, выравнивают свои скорости. У самой стенки турбулентное перемешивание парализуется наличием твердых границ, и поэтому там наблюдается значительно более быстрое падение скорости.

Измеряя разность уровней в двух пьезометрах, присоединенных к сечениям 1 и 2 трубы постоянного диаметра (рис. 30),.можно определить потерю напора между этими сечениями из уравнения Бернулли, составленного для сечений 1 и 2:

,

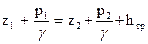откуда

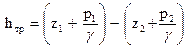. (115)

Таким образом, при равномерном движении уменьшение напора по длине трубы измеряется разностью пьезометрических высот, отсчитываемых от одной и той же горизонтальной плоскости, и, следовательно, не зависит от расположения трубы в вертикальной плоскости.

Если пропускать воду по трубе с различной скоростью и, замерив при этом потери напора, построить график h_Tp = f(v),то он будет иметь вид, представленный на рис. 31. До какого-то значения скорости потери напора изменяются прямо пропорционально скорости, а затем вид кривой внезапно меняется, и потери напора становятся пропорциональными более

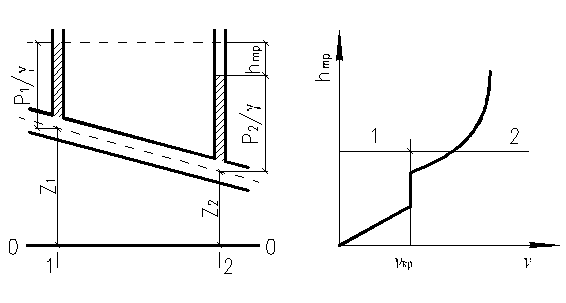
Рис. 30 – К определению потерь напора на трение в трубах

Рис. 31 – Зависимость потерь напора на трение от скорости движения жидкости 1 – ламинарный режим; 2 – турбулентный режим

высокой степени скорости (примерно ее квадрату).

Как и следовало ожидать, переход от одного закона к другому происходит при значении скорости, равном критическому, т. е. в момент перехода от ламинарного движения к турбулентному. Отсюда можно сделать важный вывод о том, что при ламинарном движении потери напора пропорциональны скорости в первой степени, а при турбулентном – скорости в степени, большей единицы.

Таким образом, ламинарный и турбулентный режим по существу отличаются не только характером движения частиц (наличием поперечных скоростей при турбулентном движении), но также особенностями распределения скоростей по сечению и характером зависимости между потерями напора и скоростью.

5.6. Потери напора на трение в круглой трубе

Найдем потери напора на трение при ламинарном движении жидкости в круглой трубе.

С учетом 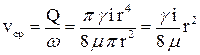можно получить выражение для гидравлического уклона в виде

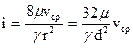
или

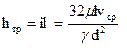. (116)

Заменяя абсолютную вязкость μ через кинематическую n, получаем формулу, называемую формулой Пуазейля - Гагена, для потерь напора при ламинарном движении:

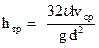. (117)

Эта формула показывает, что потери напора на трение при ламинарном режиме пропорциональны средней скорости движения. Эти потери не зависят от состояния внутренней поверхности стенок трубы, так как характеристика состояния стенок в формулу (117) не входит. Отсутствие влияния стенок на сопротивление можно объяснить тем, что жидкость прилипает к стенкам, в результате чего происходит трение жидкости о жидкость, а не жидкости о стенку.

Дата добавления: 2014-12-26