Свойства операций над множествами. Из определений объединения и пересечения множеств следует, что операции пересечения и объединения обладают следующими свойствами:

Из определений объединения и пересечения множеств следует, что операции пересечения и объединения обладают следующими свойствами:

1. Коммутативность.

A È B=B È A
A Ç B=B Ç A

2. Ассоциативность.

(A È B) È C=A È (B È C)
(A Ç B) Ç C= A Ç (B Ç C)

3. Дистрибутивность.

(A È B) Ç C = (A Ç C) È (B Ç C)
(A Ç B) È C= (A È C) Ç (B È C)

A È A=A, A Ç A=A
A È Æ = A, A Ç Æ= Æ

4. Законы де Моргана (законы двойственности).

1) A È B= A Ç B
2) A Ç B= A È B

Заметим, что закон ассоциативности при комбинировании операций объединения и вычитания, вообще говоря, не имеет места.

Пример 4. A = {1; 2; 3; 4}, B = {3; 4; 5; 6}.
A \ B= {1; 2}
(A \ B) È B= {1; 2; 3; 4; 5; 6} ¹ A
Но (A \ B) È B= A Û B Ì A

Декартово произведение двух множеств: X ´ Y: = {(x,y): x Î X и y Î Y }.

Из определения декартова произведения следует, что, вообще говоря,

X ´ Y ¹ Y ´ X,

равенство будет, если X = Y, в этом случае вместо X ´ X записывают X ².

Задание для практической работы по теме «Выполнение операций над множествами»

Заданы множества А, В, U. Выполните над ними следующие операции.

1. A È B,

2. A Ç B,

3. A \ B,

4. ,

5. A È B,

6. A Ç B,

7. (U \ B) Ç B,

8. A È (U \ B)

Вариант 1. A = {2; 3; 4}, B = {1,3; 4; 5; 6}, U={1,2,3,4,5,6,7,8,9,10},

Вариант 2. A = {1; 3; 4;9}, B = {3; 4; 5; 6,9}, U={1,2,3,4,5,6,7,8,9,10},

Вариант 3. A = {2; 3; 7;10}, B = {1; 3; 4; 5; 6}, U={1,2,3,4,5,6,7,8,9,10},

Вариант 4. A = {1; 2; 3; 5,7}, B = {3; 4; 5; 8}, U={1,2,3,4,5,6,7,8,9,10},

Вариант 5. A = {1; 2; 5; 8}, B = {3; 4; 5; 6;10}, U={1,2,3,4,5,6,7,8,9,10}.

Практическое занятие №15

Тема 3.2: « определение основных характеристик графа».

Цель: Представить в виде графа определенную систему или объект

Теоретический материал :

В математической теории графов и информатике граф — это совокупность непустого множества вершин и множества пар вершин (связей между вершинами).

На рисунке неориентированный граф с шестью вершинами и семью рёбрами.

Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах. Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами. Например, строение Википедии можно смоделировать при помощи ориентированного графа (орграф), в котором

Граф, или неориентированный граф G — это упорядоченная пара G: = (V, E), для которой выполнены следующие условия:

· V — это непустое множество вершин, или узлов,

· E — это множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами.

Вершины и рёбра графа называются также элементами графа, число вершин в графе | V | — порядком, число рёбер | E | — размером графа.

Вершины u и v называются концевыми вершинами (или просто концами) ребра e = { u, v }. Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними. Два ребра называются смежными, если они имеют общую концевую вершину. Два ребра называются кратными, если множества их концевых вершин совпадают. Ребро называется петлёй, если его концы совпадают, то есть e = { v, v }. Степенью deg V вершины V называют количество инцидентных ей рёбер(при этом петли считают дважды). Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.

неориентированный граф Ориентированный граф

Ориентированный граф (сокращённо орграф) G — это упорядоченная пара G: = (V, A), для которой выполнены следующие условия:

V — это непустое множество вершин или узлов,

A — это множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами.

Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга 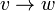ведёт от вершины v к вершине w. Смешанный граф G — это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые — неориентированными. Записывается упорядоченной тройкой G: = (V, E, A), где V, E и A определены так же, как выше. Ориентированный и неориентированный графы являются частными случаями смешанного. Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром. Ориентированным путём в орграфе называют конечную последовательность вершин v_i , для которой все пары (v_i, v_{i + 1}) являются (ориентированными) рёбрами. Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины u и v являются концами некоторого ребра, то согласно данному определению, последовательность (u, v, u) является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.

Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что:

- Всякий путь, соединяющий две вершины, содержит элементарный путь, соединяющий те же две вершины.

- Всякий простой неэлементарный путь содержит элементарный цикл.

- Всякий простой цикл, проходящий через некоторую вершину (или ребро), содержит элементарный (под-)цикл, проходящий через ту же вершину (или ребро).

- Петля — элементарный цикл.

- Бинарное отношение на множестве вершин графа, заданное как «существует путь из u в v», является отношением эквивалентности и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины. Всякий максимальный связный подграф графа G называется связной компонентой (или просто компонентой) графа G. Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов. Ребро графа называется мостом, если его удаление увеличивает число компонент.

Граф называется:

- связным, если для любых вершин u,v есть путь из u в v.

- сильно связным или ориентированно связным, если он ориентированный, и из любой вершины в любую другую имеется ориентированный путь.

- деревом, если он связный и не содержит простых циклов.

- полным, если любые его две (различные, если не допускаются петли) вершины соединены ребром.

- двудольным, если его вершины можно разбить на два непересекающихся подмножества V1 и V2 так, что всякое ребро соединяет вершину из V1 с вершиной из V2.

- k-дольным, если его вершины можно разбить на k непересекающихся подмножества V1, V2, …, Vk так, что не будет рёбер, соединяющих вершины одного и того же подмножества.

- полным двудольным, если каждая вершина одного подмножества соединена ребром с каждой вершиной другого подмножества.

- планарным, если граф можно изобразить диаграммой на плоскости без пересечений рёбер.

- взвешенным, если каждому ребру графа поставлено в соответствие некоторое число, называемое весом ребра.

- Задание для практической работы по теме «Основные понятия теории графов»: представить в виде графа свою семью до 2-го поколения и дать ему полную характеристику: количество вершин, ребер, вид и название графа.

Раздел 4. Численное дифференцирование И ИНТЕГРИРОВАНИЕ.

Практическая работа № 16

Тема 4.1: «Нахождение значения производной функции в точке Х по заданной таблично функции у=f(х) методом численного дифференцирования».

Цель: Находить значение производной функции в точке Х по заданной таблично функции у=f(х) методом численного дифференцирования.

Дата добавления: 2014-12-26