Законы распределения. Понятие гистограммы. Проверка распределения на нормальность

Случайная величина – переменная, которая может принимать те или иные значения в зависимости от различных обстоятельств.

В теории вероятностей различают два основных класса случайных величин:

1. Дискретные величины, множество значений которых представляет собой конечную или счетную последовательность;

2. Непрерывные величины, значения которых принадлежат к некоторому диапазону и могут отличаться друг от друга на сколь угодно малую величину.

Для полной характеристики случайной величины должны быть заданы (или определены) не только все ее значения, но и вероятности p_i (I = 1, 2, …, n), с которыми случайная величина принимает каждое из них, т.е. p_i = P(X = x_i).

Функция р(х), связывающая значения случайной величины с соответствующими им вероятностями, представляет собой закон распределения случайной величины [6].

Однако, задать случайную величину можно и иначе, например, так называемой функцией распределения.

Функцией распределения случайной величины Y называется функция F(x), выражающая для каждого х вероятность того, что случайная величина Y примет какое-нибудь значение, меньшее х.

F(x) = P(X<x).

Наряду с выборочным средним и дисперсией, функция распределения является важным показателем закона распределения.

В зависимости от того, о каком классе величин идет речь, выделяют дискретные и непрерывные распределения.

Дискретные распределения.

Большинство дискретных распределений проистекают от схемы испытаний Бернулли с двумя исходами успех-неуспех, в которой вероятность успеха Р в каждом испытании не зависит от предшествующих испытаний.

Биноминальное распределение имеет случайная величина Х, представляющая число успехов в последовательности из n независимых испытаний. Если n велико, а Р мало, то распределение Х приближается к распределению Пуассона со средним, равным: . Дисперсия вычисляется по формуле: .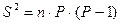

Функция распределения[7]: .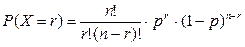

Геометрическое распределение имеет случайная величина, представляющая число испытаний до первого успеха.

Среднее значение: 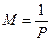, дисперсия: .

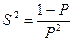Отрицательное биномиальное распределение имеет случайная величина X, представляющая число испытаний до k успехов. Этому распределению хорошо соответствуют данные о числе объектов, с которыми за фиксированный промежуток времени случилось 0,1,2,3,... инцидента (аварии, несчастные случаи и т.п.). Если k велико, а P близко к 1, то Х приближается к распределению Пуассона со средним 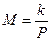и дисперсией .

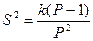Гипергеометрическое распределение имеет случайная величина, представляющая число успехов в случайной выборке размера n из совокупности размера N (N>n), в которой содержится S успехов (или оценка вероятности успеха равна P=S/N).

Среднее значение: , дисперсия: .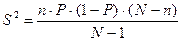

Распределение Пуассона имеет случайная величина, представляющая число событий на заданном интервале (времени, пространства), когда среднее число событий в минимальном дискрете (частота или интенсивность событий) равна L.

Непрерывные распределения.

Нормальное или Гауссово распределение является наиболее распространенным, поскольку оно пригодно для описания широкого класса явлений, каждое из которых определяется взаимодействием большого числа разнородных факторов. Эта универсальность объясняется так называемой предельной теоремой: распределение суммы n произвольно распределенных случайных величин стремится к нормальному распределению при увеличении n. Нормальное распределение определяется двумя параметрами: средним и дисперсией.

Логнормальное распределение характеризуется двумя параметрами: средним значением a и масштабом k, определено для положительных Х и связано с нормальным распределением преобразованием LN(X).

Экспоненциальное распределение (называемое также обратным экспоненциальным или показательным) имеет случайная величина, представляющая интервалы между событиями, когда сами события имеют пуассоново распределение с интенсивностью L>0.

Следующие четыре распределения принадлежат к так называемой группе экспоненциальных распределений (поскольку в формулах функции вероятности явно фигурируют экспоненты) и имеют свои специальные области практического приложения (радиотехника, теория надежности, биология и пр.):

- распределение Релея характеризуется одним параметром масштаба k, определено для положительных Х и является частным случаем распределения Вейбулла с параметром формы с=2;

- распределение Вейбулла характеризуется двумя параметрами: формы c и масштаба k и определено для положительных Х;

- распределения логистическое и экстремальных значений характеризуются двумя параметрами: средним значением a и масштабом k, причем первое распределение определено для всех Х, а второе имеет верхнее ограничение X<=a+2*k;

Последние три распределения из группы гамма-распределений носят более академичный характер, но часто используются в качестве аргументов различных математических и статистических вычислений:

- распределение Эрланга характеризуется двумя параметрами: формы c и масштаба k и определено для положительных Х;

- распределение гамма характеризуется двумя параметрами: формы c и масштаба k и определено для положительных Х;

- распределение бета характеризуется двумя параметрами a, b и определено для положительных Х.

Закон распределения случайной величины можно задать, используя не только табличный (ряд распределения) способ, но и графический (график функции распределения).

Гистограмма – форма столбчатой диаграммы, на которой значения пере­менной размещаются по оси абсцисс или оси X, а частота или относительная частота появления значений указыва­ется по оси ординат или оси Y.

Например, в случае гистограммы распределения суммарного тестового балла по оси абсцисс откладываются сырые баллы – первичные показатели суммарных баллов, возможных по данному тесту, по оси ординат – относительные частоты (проценты) встречаемости суммарных баллов в выборке стандартизации.

Гистограмма является общеупотребительной формой представления выборочного распределения. Для ее вычисления диапазон изменения выборочных значений разбивают на некоторое число равных интервалов и подсчитывают число значений в каждом из них. Обычно для расчета количества (k) и длины интервалов (λ) при числе n -измерений используется формула Стерджесса:

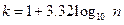
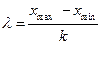
При графическом представлении гистограммы на каждом интервале строится прямоугольник (столбец), высота которого пропорциональна числу выборочных значений в интервале.

Если приблизить размер выборки и число интервалов к бесконечности, то гистограмма будет приближаться к кривой плотности вероятности распределения значений исследуемой переменной.

Проверка выборочного распределения на нормальность может быть проведена несколькими способами, которые дополняют друг друга:

1. Глазомерный метод в качестве предварительной субъективной оценки может быть осуществлен по рисунку гистограммы выборочного распределения с наложенной кривой плотности вероятности нормального распределения.

Гистограмма позволяет "на глаз" оценить нормальность эмпирического распределения. На гистограмму также накладывается кривая нормального распределения. Гистограмма позволяет качественно оценить различные характеристики распределения. Например, на ней можно увидеть, что распределение бимодально (имеет 2 пика). Это может быть вызвано, например, тем, что выборка неоднородна, возможно, извлечена из двух разных популяций, каждая из которых более или менее нормальна. В таких ситуациях, чтобы понять природу наблюдаемых переменных, можно попытаться найти качественный способ разделения выборки на две части.

2. Проверка нулевой гипотезы соответствия распределений по коэффициентам асимметрии и эксцесса.

Важным способом "описания" переменной является форма ее распределения, которая показывает, с какой частотой значения переменной попадают в определенные интервалы. Эти интервалы, называемые интервалами группировки, выбираются исследователем. Обычно исследователя интересует, насколько точно распределение можно аппроксимировать нормальным. Простые описательные статистики дают об этом некоторую информацию.

Например, если асимметрия (показывающая отклонение распределения от симметричного) существенно отличается от 0, то распределение несимметрично, в то время как нормальное распределение абсолютно симметрично. Итак, у симметричного распределения асимметрия равна 0. Асимметрия распределения с длинным правым хвостом положительна. Если распределение имеет длинный левый хвост, то его асимметрия отрицательна. Асимметрия кривой эмпирического распределения определяется по формуле:

,

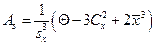где 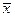– среднее арифметическое, S_x – стандартное отклонение, Θ – среднее кубическое 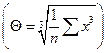, С – среднее квадратическое .

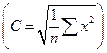Далее, если эксцесс (показывающий "остроту пика" распределения) существенно отличен от 0, то распределение имеет или более закругленный пик, чем нормальное, или, напротив, имеет более острый пик (возможно, имеется несколько пиков). Обычно, если эксцесс положителен, то пик заострен, если отрицательный, то пик закруглен. Эксцесс нормального распределения равен 0. Эксцесс кривой определяется по формуле:

,

где Q – среднее значение четвертой степени .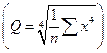

Проверку статистической значимости вычисляемого показателя асимметрии можно провести на основании общего неравенства Чебышева:

,

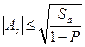где S_a – дисперсия эмпирической оценки асимметрии: ; P – уровень значимости или вероятность (Р) ошибки первого рода – ошибочного вывода о незначимости асимметрии при наличии значимой асимметрии (Р = 0,05 или Р = 0,01).

Аналогично оценивается значение эксцесса:

,

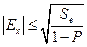где S_e – эмпирическая дисперсия оценки эксцесса: .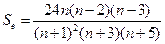

3. Проверка соответствия формы распределений по критериям Колмогорова, омега–квадрат и хи–квадрат.

Критерий Колмогорова реагирует на наибольшую разность между распределениями, которая обычно проявляется вблизи максимума функции плотности вероятности, поэтому он плохо приспособлен для выявления различий на концах распределений.

Критерий омега–квадрат является более равномерным, учитывая различия между распределениями на всем интервале выборочных значений, однако он сравнительно менее исследован в плане составления таблиц критических значений и предельных аппроксимаций для различного типа распределений.

Критерий хи–квадрат также достаточно равномерно учитывает различия на всем диапазоне выборочных значений, однако требует большей осторожности при своем применении к непрерывным распределениям, поскольку его результаты существенно зависят от объема выборки и от разбиения выборочного пространства на интервалы.

Используемые аппроксимации критерием для вычисления уровня значимости получены в предположении «n стремится к бесконечности» и достаточно точны для больших выборок (n>30–40) и в области значений P=0.15–0.01.

В итоге остался открытым ряд вопросов:

– почему так важно нормальное распределение;

– как нормальное распределение используется в статистических рассуждениях;

– как узнать последствия нарушений предположений нормальности?

Нормальное распределение важно по многим причинам. В большинстве случаев оно является хорошим приближением уже известных функций (Колмогорова, омега-квадрат, хи-квадрат и др.). Распределение многих статистик является нормальным или может быть получено из нормальных с помощью некоторых преобразований. Рассуждая философски, можно сказать, что нормальное распределение представляет собой одну из эмпирически проверенных истин относительно общей природы действительности и его положение может рассматриваться как один из фундаментальных законов природы. Точная форма нормального распределения (характерная "колоколообразная кривая") определяется только двумя параметрами: средним и стандартным отклонением.

Характерное свойство нормального распределения состоит в том, что 68% всех его наблюдений лежат в диапазоне ±1 стандартное отклонение от среднего, а диапазон ±2 стандартных отклонения содержит 95% значений. Другими словами, при нормальном распределении, стандартизованные наблюдения[8], меньшие -2 или большие +2, имеют относительную частоту менее 5%.

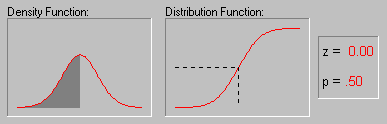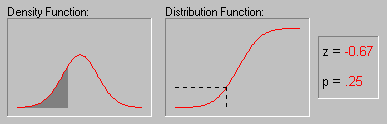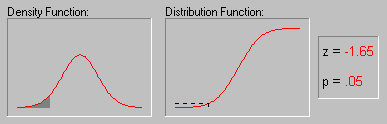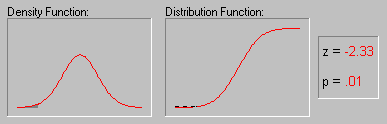
Для иллюстрации того, как нормальное распределение используется в статистических рассуждениях (индукция) приведем пример. Пары выборок мужчин и женщин выбирались из совокупности, в которой среднее значение лейкоцитов в крови для мужчин и женщин было в точности одно и то же. Хотя наиболее вероятный результат таких экспериментов (одна пара выборок на эксперимент) состоит в том, что разность между средними значениями лейкоцитов в крови для мужчин и женщин для каждой пары близка к 0, время от время появляются пары выборок, в которых эта разность существенно отличается от 0. Как часто это происходит? Если объем выборок достаточно большой, то, зная, что разности "нормально распределены" и зная форму нормальной кривой, вы можете точно рассчитать вероятность случайного получения результатов, представляющих различные уровни отклонения среднего от 0 - значения гипотетического для всей популяции. Если вычисленная вероятность настолько мала, что удовлетворяет принятому заранее уровню значимости, то можно сделать лишь один вывод: ваш результат лучше описывает свойства популяции, чем "нулевая гипотеза". Следует помнить, что нулевая гипотеза рассматривается только по техническим соображениям как начальная точка, с которой сопоставляются эмпирические результаты. Отметим, что все это рассуждение основано на предположении о нормальности распределения этих повторных выборок (т.е. нормальности выборочного распределения).

Для того, чтобы узнать последствия нарушений предположений нормальности, необходимо воспользоваться так называемыми экспериментами Монте-Карло, так как последствия могут быть продемонстрированы только эмпирически. В этих экспериментах большое число выборок генерируется на компьютере, а результаты, полученные из этих выборок, анализируются с помощью различных тестов. Этим способом можно эмпирически оценить тип и величину ошибок или смещений, которые вы получаете, когда нарушаются определенные теоретические предположения тестов, используемых вами. Исследования с помощью методов Монте-Карло интенсивно использовались для того, чтобы оценить, насколько тесты, основанные на предположении нормальности, чувствительны к различным нарушениям предположений нормальности. Общий вывод этих исследований состоит в том, что последствия нарушения предположения нормальности менее фатальны, чем первоначально предполагалось. Хотя эти выводы не означают, что предположения нормальности можно игнорировать, они увеличили общую популярность тестов, основанных на нормальном распределении.

Дата добавления: 2014-12-26