
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Степень числа. Квадрат и куб числа
Упрощение выражений.
 Рассмотрим два выражения: (2 + 4) • 3 и 2 • 3 + 4 • 3 Оба выражения равны 18: (2 + 4) • 3 = 6 • 3 = 18; 2 • 3 + 4 • 3 = 6 + 12 = 18. Получается, что: (2 + 4) • 3 = 2 • 3 + 4 • 3. Для того чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения. Это правило называется распределительным свойством умножения относительно сложения.
С помощью букв его записывают так: (a + b) • c = a • c + b • c. Рассмотрим два выражения: (2 + 4) • 3 и 2 • 3 + 4 • 3 Оба выражения равны 18: (2 + 4) • 3 = 6 • 3 = 18; 2 • 3 + 4 • 3 = 6 + 12 = 18. Получается, что: (2 + 4) • 3 = 2 • 3 + 4 • 3. Для того чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения. Это правило называется распределительным свойством умножения относительно сложения.
С помощью букв его записывают так: (a + b) • c = a • c + b • c.
| |
Порядок выполнения действий.
|
Степень натурального числа а
Степенью натурального числа a называют произведение нескольких множителей, каждый из которых равен а. Например: 
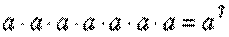
Квадрат числа а
Произведение a умножить на a называют второй степенью или квадратом числа a.

И другие квадраты чисел также можете легко найти.
Куб числа а
Произведение числа a на a и на a называют третьей степенью или кубом числа a. Записывают таким образом,. Читают a в кубе или a в третьей степени.

МАГИЧЕСКИЙ КВАДРАТ
ИСТОРИЯ ВОЗНИКНОВЕНИЯ И РАЗВИТИЯ МАГИЧЕСКИХ КВАДРАТОВ
Понятием «магия» принято считать различные человеческие действия, которые имеют целью влиять сверхъестественным образом на тот или иной материальный предмет или явление.
Числовую фигуру обычно называют магической, если составляющие ее числа не повторяются и при определенных взаимных сочетаниях дают заранее задуманный составителем результат.
Наверное, одной из первых известных человечеству магических фигур является магический квадрат. Он встречаются в культуре, истории, верованиях и в различных мистических учениях многих народов.
Страна, в которой был впервые придуман магический квадрат, точно неизвестна, неизвестен век, даже тысячелетие нельзя установить точно. Вероятно, самым «старым» из дошедших до нас магических квадратов является таблица Ло Шу (ок. 2200 г. до н. э.). Она имеет размер 3x3 и заполнена натуральными числами от 1 до 9. В этом квадрате сумма чисел в каждой строке, столбце и диагонали равна 15 (рис. 1). Согласно одной из легенд, прообразом Ло Шу стал узор из связанных черных и белых точек, украшавший панцирь огромной черепахи, которую встретил однажды на берегу реки Ло-Шуй мифический прародитель китайской цивилизации Фуси.
Жители Поднебесной считали таблицу Ло Шу священной, у них даже не возникало мысли о составлении аналогичных квадратов большего размера, поэтому последние стали появляться только три тысячелетия спустя.

Рис. 1. Таблица Ло Шу.
В XI в. из Китая магические квадраты распространились сначала в Индию, затем в Японию. Из Индии увлечение магическими квадратами перешло к арабам. Именно от арабов квадраты получили название «магические».
На востоке их считали волшебными, полными тайного смысла символами, и использовали при заклинаниях. Магические квадраты находят при раскопках поселений Золотой Орды (рис. 2), в Китае, Индии и Тибете, в Израиле, Турции и во всех странах Европы.

Рис. 2. Магический квадрат, найденный при раскопках поселений Золотой Орды
Европейцев с магическими квадратами познакомил в XV веке византийский писатель Э. Мосхопулос. Первым квадратом, придуманным европейцем, считается квадрат А. Дюрера, изображенный на его знаменитой гравюре «Меланхолия» (рис. 3).

Рис. 3. Гравюра «Меланхолия»
Дата создания гравюры - 1514 год - указана числами, стоящими в двух центральных клетках нижней строки.
В западной Европе в средние века магические квадраты были достоянием представителей алхимии и астрологии. Магическим квадратам приписывали различные мистические свойства. Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы (рис. 4)

Рис. 4. Старинный оберег с изображением магического квадрата
В XIX и XX вв. интерес к магическим квадратам вспыхнул с новой силой. Их стали исследовать с помощью методов высшей алгебры и операционного исчисления.
С развитием вычислительной техники исследования магических квадратов в последние десятилетия приобрели второе дыхание. Вполне объяснимо, что наибольшие успехи в развитии теории и практики магических квадратов были достигнуты в Европе, США и Японии. Появились описания более сложных фигур, таких как: кубы и тессеракты – четырехмерные аналоги магических квадратов. Результаты этих исследований открывают новые методы решения сложных задач современной математики.
Свойства магических квадратов
Каждый элемент магического квадрата называется клеткой. Квадрат, сторона которого состоит из n клеток, содержит n2 клеток и называется квадратом n –го порядка. В большинстве магических квадратов используются первые n2 последовательных натуральных чисел (т.е. числа от 1 до n2). Такие квадраты называют нормальными.
Две диагонали, проходящие через центр квадрата, называются главными диагоналями.
Сумма чисел, стоящих в каждой строке, каждом столбце и на любой диагонали магического квадрата называется магической константой M. Магическая константа нормального волшебного квадрата зависит только от n и определяется формулой:

Нормальные магические квадраты существуют для всех порядков 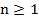 , за исключением n= 2, хотя случай n =1 тривиален — квадрат состоит из одного числа. Минимальным нетривиальным случаем является таблица Ло Шу, он имеет порядок 3. Магическая константа
, за исключением n= 2, хотя случай n =1 тривиален — квадрат состоит из одного числа. Минимальным нетривиальным случаем является таблица Ло Шу, он имеет порядок 3. Магическая константа 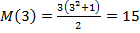 (рис. 5).
(рис. 5).
Рис. 5. Нормальный магический квадрат 3-го порядка 
Из условий построения следуют следующие, очевидные свойства магических квадратов:
1. Если все числа в клетках магического квадрата увеличить на одно и то же число  , то получим магический квадрат, с магической константой
, то получим магический квадрат, с магической константой 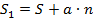 , где
, где  - магическая константа полученного квадрата,
- магическая константа полученного квадрата, 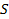 - магическая константа исходного квадрата,
- магическая константа исходного квадрата, 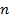 – порядок квадрата рис. 6.
– порядок квадрата рис. 6.
2. Если все числа в клетках магического квадрата умножить на одно и то же число  , то получим магический квадрат, с магической константой
, то получим магический квадрат, с магической константой  , где
, где  - магическая константа полученного квадрата,
- магическая константа полученного квадрата, 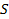 - магическая константа исходного квадрата (рис. 7).
- магическая константа исходного квадрата (рис. 7).
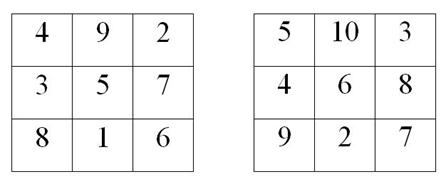
Рис. 6. Новый магический квадрат, полученный из исходного, увеличением каждого числа на 1

Рис. 7. Новый магический квадрат, полученный из исходного, умножением каждого числа на 2
3. Сумма чисел, стоящих в каждой строке, каждом столбце и на любой диагонали магического квадрата одинакова и больше или равна магической константе нормального волшебного квадрата соответствующего порядка.
4. При повороте вокруг центра на угол  магического квадрата, получим магический квадрат (рис. 8).
магического квадрата, получим магический квадрат (рис. 8).
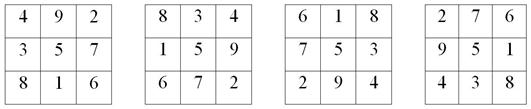
Рис. 8. Поворот магического квадрата
5. При отражении, относительно одной из осей симметрии магического квадрата получим магический квадрат (рис. 9,10).

Рис. 9. Отражение магического квадрата относительно горизонтальной (вертикальной) оси симметрии

Рис. 10. Отражение магического квадрата относительно главных диагоналей
Среди множества магических квадратов некоторые выделяются особыми свойствами: числа, из которых они составлены, удовлетворяют различным дополнительным условиям.
Магический квадрат называется ассоциативным или симметричным, если сумма любых двух чисел, расположенных симметрично относительно центра квадрата, равна  . Квадраты Ло Шу и Дюрера – симметричные.
. Квадраты Ло Шу и Дюрера – симметричные.
Для симметричных магических квадратов существует еще одно свойство:
6. При отражении строк (столбцов) симметричного магического квадрата относительно горизонтальной (вертикальной) оси симметрии получим симметричный магический квадрат (рис. 11).
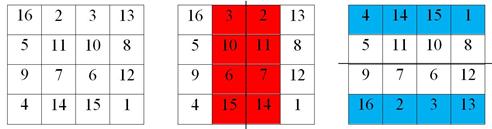
Рис. 11. Отражение столбцов (строк) магического квадрата относительно вертикальной (горизонтальной) оси
способы построения некоторых магических квадратов
С давних пор математики стремились решить две основные задачи, связанные с магическими квадратами: найти общий метод их построения и описать все возможные магические квадраты.
В XVI веке Корнелий Генрих Агриппа построил квадраты 3–го, 4–го, 5–го, 6–го, 7–го, 8–го и 9–го порядков, которые были связаны с астрологией 7 планет (ПРИЛОЖЕНИЕ А).
Основы математической теории построения магических квадратов были заложены французскими учеными в XVII в. Позже она стала излюбленной темой исследований многих авторов. И хотя для каждого вида квадрата были найдены свои способы решения задачи, пока не известен общий, пригодный для квадратов любого порядка, метод их построения.
2.1.1 Заполнение квадратов нечетных порядков (индийский способ)
Этот способ придуман, как полагают, в Индии еще до начала нашего летоисчисления. Порядок квадрата должен быть нечетным. Иначе квадрат магическим не получится.
1. Нарисуем квадратную таблицу порядка n.
2. Единицу впишем в середину верхней строки.
3. Далее, идя вверх по ломаным диагоналям, будем в квадраты ставить подряд натуральные числа.
4. Как только ломаная диагональ замкнется, то есть мы дойдем до натурального числа, кратного n, то следующее по порядку число впишем в поле под клеткой, на которой мы остановились.
Рис. 12. Магические квадраты 3-го и 5-го порядка, полученные индийским способом (ломаные диагонали закрашены одним цветом) (M (3)=15, M (5)=65)
5. И так далее, пока не переберем все числа до квадрата n.
То, что получилось - нормальный магический квадрат (рис. 12).
2.1.2. Заполнение квадрата порядка, кратного четырем
Среди квадратов четного порядка наиболее изученными являются квадраты, порядок которых делится на 4, так как они обладают рядом дополнительных свойств, которыми не обладают квадраты других порядков. Неслучайно квадрат А. Дюрера — квадрат 4-го порядка.
Для этих квадратов было разработано множество способов построения. Один из них основан на методе выделения диагональных элементов.
1. Исходный квадрат делится на соответствующее число квадратов порядка 4. В каждом подквадрате закрашиваются диагональные элементы (главная и побочная).
2. Остальные элементы построчно заполняются порядковыми целыми числами в направлении слева -направо и сверху -вниз по закрашенным клеткам и справа -налево и снизу-вверх по не закрашенным клеткам.
3. Переход между цветами при заполнении происходит, если следующая для заполнения клетка меняет цвет.
Результаты построения магических квадратов 8-го и 12-го порядка представлены на рис. 13, 14.
Рис. 13. Магический квадрат 8-го порядка, построенный способом разбиения на подквадраты 4x4 (M (8)=260)
Рис. 14. Магический квадрат 12-го порядка, построенный способом разбиения на подквадраты 4x4 (M (12)=870)
Нетрудно проверить, что полученные этим способом квадраты являются симметричными.
2.1.3. Заполнение квадрата четного порядка, не кратного четырем
Последняя группа магических квадратов – квадраты чётно-нечётного порядка n =4 k +2, k =1, 2, 3…. Иногда их ещё называют квадратами порядка одинарной чётности (в отличие от квадратов порядка двойной чётности или чётно-чётного порядка n=4 k, k =1, 2, 3…). Эти магические квадраты, наверное, меньше всего исследованы. Для этих квадратов не существует общих методов построения, хотя можно использовать метод четырех квадратов, Н. В. Макаровой.
Суть метода в следующем:
1. Исходный квадрат разбивается на 4 равных квадрата, по следующей схеме (рис. 15)
Рис. 15. Разбиение исходного квадрата на 4 подквадрата
В результате такого разбиения получим 4 квадрата нечетного порядка  , где
, где  -порядок полученных квадратов, n -порядок исходного квадрата.
-порядок полученных квадратов, n -порядок исходного квадрата.
2. Заполняем подквадрат 1, как магический квадрат нечетного порядка  числами от 1 до
числами от 1 до  (например, используя индийский способ).
(например, используя индийский способ).
3. Подквадрат 2 получаем из подквадрата 1, увеличением каждого числа 1-го подквадрата на  .
.
4. Подквадрат 3 получаем из подквадрата 2, увеличением каждого числа 2-го подквадрата на  .
.
5. Подквадрат 4 получаем из подквадрата 3, увеличением каждого числа 3-го подквадрата на  .
.
В результате таких построений получится почти магический квадрат, из которого можно получить магический, некоторой симметричной перестановкой клеток в полученном квадрате.
Применим описанный способ для построения магического квадрата 6-го порядка:
Рис. 16. Заполненный квадрат
Полученный квадрат (рис. 16), не является магическим, т.к. суммы по строкам и по диагоналям не равны магической постоянной  =111.
=111.
Поменяем местами числа, отмеченные одинаковым цветом в первом и во втором столбце (т.е. фигуру образованную числами 8, 5, 4 на фигуру образованную числами 35, 32, 31). Рис. 17.
Рис. 17. Клетки, для которых необходим обмен значениями, помечены одинаковым цветом
В итоге получим магический квадрат (рис. 18).
Рис. 18. Построенный магический квадрат 6-го порядка 
СПОСОБЫ РЕШЕНИЯ ЛОГИЧЕСКИХ ЗАДАЧ
Основной прием, который используется при решении текстовых логических задач, заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи. Приглашаем познакомиться с примером решения конкретной задачи методом таблиц.

| ||
|
|
|
Дата добавления: 2014-12-27; Просмотров: 2043; Нарушение авторских прав?; Мы поможем в написании вашей работы!
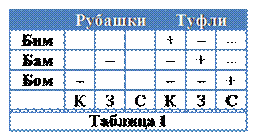 Далее, туфли и рубашка Бома не являются красными, отметим соответствующие ячейки таблицы знаком –. Из таблицы, заполненной на этом этапе, видим, что красные туфли могут быть только у Бима, а, следовательно, туфли Бома - синие. Правая часть таблицы заполнена, мы установили цвета обуви клоунов (табл.1). Цвет рубашки Бима совпадает с цветом его туфель и является красным. Теперь легко устанавливается владелец зеленой рубашки - Бом. Бам, в таком случае, одет в рубашку синего цвета.
Мы полностью заполнили таблицу, в которой однозначно устанавли-ваются цвета туфель и рубашек клоунов (см. табл. 2): Бим одет в красную рубашку и красные туфли, Бам в синей рубашке и зеленых туфлях, Бом в зеленой рубашке и туфлях синего цвета.
Далее, туфли и рубашка Бома не являются красными, отметим соответствующие ячейки таблицы знаком –. Из таблицы, заполненной на этом этапе, видим, что красные туфли могут быть только у Бима, а, следовательно, туфли Бома - синие. Правая часть таблицы заполнена, мы установили цвета обуви клоунов (табл.1). Цвет рубашки Бима совпадает с цветом его туфель и является красным. Теперь легко устанавливается владелец зеленой рубашки - Бом. Бам, в таком случае, одет в рубашку синего цвета.
Мы полностью заполнили таблицу, в которой однозначно устанавли-ваются цвета туфель и рубашек клоунов (см. табл. 2): Бим одет в красную рубашку и красные туфли, Бам в синей рубашке и зеленых туфлях, Бом в зеленой рубашке и туфлях синего цвета.
 Ответ: Бим одет в красную рубашку и красные туфли, Бам в синей рубашке и зеленых туфлях, Бом в зеленой рубашке и туфлях синего цвета.
Ответ: Бим одет в красную рубашку и красные туфли, Бам в синей рубашке и зеленых туфлях, Бом в зеленой рубашке и туфлях синего цвета.