Уравнения прямой в пространстве и на плоскости

Всякий вектор, лежащий на прямой или на прямой, параллельной данной прямой, называется направляющим вектором данной прямой. Запишем уравнение прямой, проходящей через точку 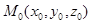и имеющей

направляющий вектор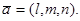

Пусть 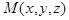- произвольная точка этой прямой. Тогда векторы и коллинеарны, т.е. где t - некоторый параметр.

Т.к. = 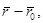то

. (1)

Уравнение (1) называют векторным параметрическим уравнением прямой (сравним с (14) §6). Поскольку 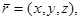то из (1) получим параметрические уравнения прямой

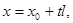
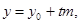
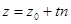. (2)

Из (2) получим

. (3)

Уравнения (3) называют каноническими уравнениями прямой.

Пример. Записать уравнение прямой, проходящей через две данные точк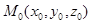и и .

Решение. Вектор = возьмем в качестве направляющего. Тогда

. (4)

Уравнения (4) -искомые уравнения.

Две плоскости пересекаются по прямой, поэтому система двух уравнений 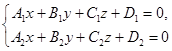(5)

определяет прямую в пространстве. Перейдем от уравнений (5) к каноническим уравнениям прямой.

Поскольку нормали и перпендикулярны соответствующим плоскостям, то вектор коллинеарен их линии пересечения. Тогда вектор 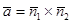можно взять за направляющий вектор прямой.

Раскрывая векторное произведение 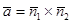, получим координаты направляющего вектора

. (6)

Если () - некоторое решение системы (5), то параметрические уравнения прямой совпадют с (2), l,m,n определяются формулами (6).

Рассмотрим теперь уравнение прямой в плоскости xОy, т.е. в плоскости z = 0. В этом случае уравнение (5) перепишем в виде (7)

Если заранее оговорить условие, что прямая лежит в плоскости z = 0, то второе уравнение в (7) можно опустить. В результате получим уравнение . (8)

Уравнение (8) называют общим уравнением прямой на плоскости xOy. Если то из (8) получим

. (9)

Уравнение (9) называют уравнением прямой с угловым коэффициентом , где - угол между прямой и осью Ox.

Найдем угол между двумя прямыми , .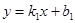

Поскольку то ,

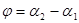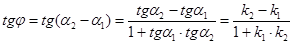(10)

Из равенства (10) можно получить условие параллельности и перпендикулярности двух прямых на плоскости:

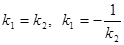. (11)

Нормальное уравнение прямой и уравнение в отрезках на плоскости получаются из соответствующих уравнений плоскости при z = 0. Отклонение точки от прямой также получается из соответствующей формулы для плоскости при z = 0.

Дата добавления: 2014-12-27