Обобщенное уравнение метода усреднения

Пусть дана система обыкновенных дифференциальных урав­нений 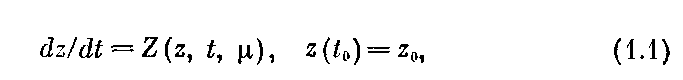где есть n-мерные векторы, 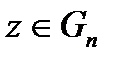, 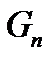—некоторая n-мерная область евклидова пространства 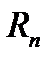, , 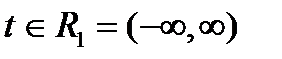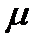— малый неотрицательный параметр. Наряду с системой (1) зададим другую систему обыкновен­ных дифференциальных уравнений

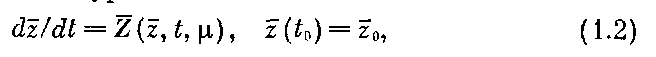
которую будем называть системой сравнения для системы (1). Вектор-функцию 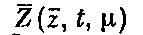назовем функцией сравнения для .

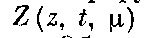Обычно уравнения сравнения строятся с помощью какого-либо оператора сглаживания (оператора усреднения).

Общая задача, которую предстоит решить, состоит в том, что­бы найти такую невырожденную дифференцируемую замену переменных 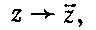которая преобразует систему (1) в систему сравнения (2). Расскажем коротко идею решения.

Пусть искомая замена переменных представляется в виде

Тогда справедливо дифференциальное тождество

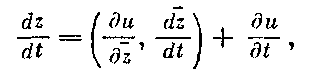
и, пользуясь первоначальной системой (1) и системой сравне­ния (2), получаем то уравнение, которому должна удовлетворять неизвестная вектор-функция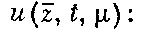

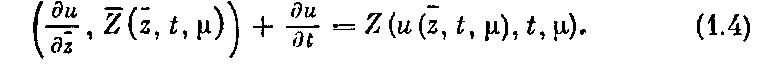
Первое слагаемое в (4) представляет собой произведение матрицы Якоби порядка nХn па вектор-столбец 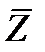. Уравнение (4) назовем обобщенным уравнением метода усреднения или обобщенным уравнением Крылова — Боголюбова.

U координатной форме уравнение (4) имеет вид

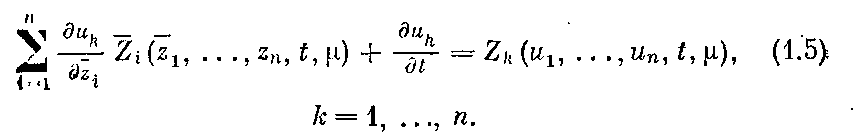
К уравнениям (4) или (5) следует добавить начальные условия

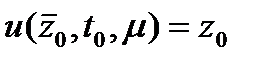(1.6)

Таким образом, замена переменных (3) определяется систе­мой n квазилинейных уравнений в частных производных первого Порядка с искомыми функциями 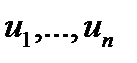и с начальными ус­ловиями (6).

Если преобразование (3) существует и не вырождено в не­которой области изменения переменных 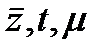, то в этой области уравнении (1) и (2) являются эквивалентными (равносиль­ными).

Отыскание точных решений систем (2) и (4) является, инк правило, задачей такой же трудности, как и решение первоначальных уравнений, однако при построении приближенных решении уравнений (1) и в особенности уравнений (2) замена переменных (3) и уравнение (4) могут оказаться, как будет показанo ниже, весьма полезными.

Сущность метода усреднения

При построении уравнений сравнения (2) мы всегда должны иметь в виду по крайней мере два обстоятельства:

1) Уравнения сравнения должны, быть более «решабельными», нежели первоначальные уравнения, иначе процедура заме­ны одних уравнений другими теряет смысл.

2) Следует иметь в распоряжении методы, оценивающие от­клонении решений уравнений сравнения от первоначальных ре­шений. Желательно, чтобы эти отклонения были достаточно ма­лыми, и это обстоятельство оказывается непосредственно связан­ным с изучением свойств вектор-функции преобразования 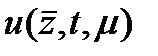, т. е. свойств решения уравнения Крылова — Боголю­бов (4).

Чтобы пояснить эти обстоятельства, рассмотрим два предель­ных и некотором смысле варианта.

Первый вариант — тождественное преобразование. Пусть уравнения сравнения (2) в точности совпадают с первоначаль­ными уравнениями, т. е. 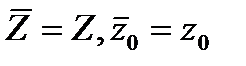Тогда уравнение (4) принимает вид

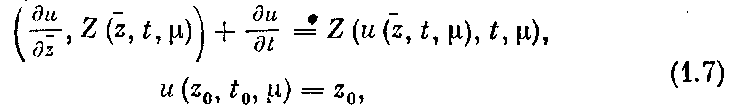
и оно, как легко проверить, допускает решение , т. е. старые и новые переменные совпадают, 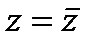. Таким обра­зом, в случае равенства функций Z и 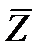мы легко находим одно из частных решений уравнения Крылова — Боголюбова, но от этого решения мало пользы, так как не получено никакой новой информации о свойствах решений исходных уравнений.

Второй вариант — это преобразование, приводящее к простей­шим уравнениям сравнения. Самым простым уравнением срав­нения можно считать уравнение

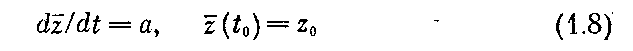
(а — постоянный вектор), имеющее очевидное решение

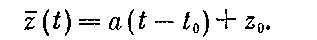
Изучим теперь уравнение Крылова — Боголюбова для этого случая. Оно запишется в виде

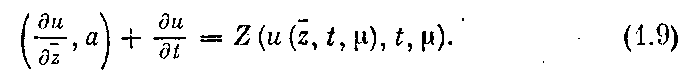
Система в характеристиках для (9) имеет вид

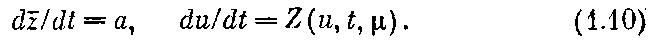
Отсюда следует, что определение замены переменных, преобра­зующей первоначальное уравнение (1) в простейшее уравнение (8), предполагает знание решения первоначальной системы. Сле­довательно, нахождение решения уравнения Крылова — Боголю­бова в этом случае эквивалентно нахождению решения исходной системы (1), поэтому решение задачи о преобразовании урав­нений не стало более легким.

Рассмотренные здесь предельные варианты позволяют сделать следующие выводы.

С одной стороны, уравнение Крылова — Боголюбова (7) при тождественном преобразовании правых частей имеет очевидное решение, но зато уравнения сравнения совпадают с первоначаль­ными, и, следовательно, проблема интегрируемости уравнений сравнения равносильна проблеме интегрируемости первоначальных уравнений. С другой стороны, если в качестве уравнений сравнения выбираются простейшие, то решение уравнений, оп­ределяющих замену переменных, эквивалентно интегрированию первоначальных уравнений.

Эти соображения наталкивают на мысль о нахождении про­межуточного, компромиссного варианта, сущность которого долж­на состоять в следующем.

1) Функцию сравнения 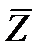следует выбрать таким образом, чтобы она имела более простую аналитическую структуру по сравнению с первоначальной функцией Z, но вместе с тем ей должны быть присущи основные свойства последней. Только при таком выборе можно ожидать некоего сходства в поведении решений уравнения сравнения и решений первоначального уравнения.

2) Выбор функции сравнения 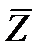должен осуществляться та­ким образом, чтобы квазилинейные уравнения в частных производных для замены переменных (уравнения Крылова — Бого­любова) допускали если не нахождение точного решения, то хо­ти бы проведение какого-либо качественного анализа.

В первую очередь нас будут интересовать такие свойства функции 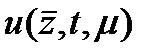как ограниченность и степень гладкости в некоторой области изменения аргументов.

Набегая вперед, представим себе, что нам удалось, с одной стороны, построить приближенное решение 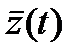уравнения срав­нения (2), а с другой — оценить норму 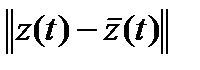на некото­ром промежутке времени 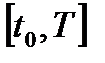. Тогда, очевидно, можно сделать и некоторые выводы о поведении решения z(t) первоначальной системы (1) на этом промежутке времени.

Такой компромиссный вариант, как мы увидим дальше, часто в конкретных задачах может быть реализован и дает неплохие для приложений результаты. Можно сказать, что этот подход и выражает собой сущность прикладного аспекта преобразования Крылова- Боголюбова для систем обыкновенных дифференциальных уравнений вида (1).

5) 1. МЕТОД РАЗМЕРНОСТЕЙ И ЕГО ПРИЛОЖЕНИЕ К ПОСТРОЕНИЮ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ.

О СТРУКТУРЕ ФУНКЦИОНАЛЬНОЙ СВЯЗИ

Многие закономерности, устанавливаемые наукой, представ­ляют собой функциональные зависимости между размерными (именованными) величинами, характеризующими процессы, явле­ния или объекты, понимаемые в самом широком смысле. Это об­стоятельство накладывает соответствующие ограничения на струк­туру функциональной связи и = f(x,y): размерности левой и пра­вой части равенства должны быть одинаковы. Именно этот факт во многих случаях позволяет устанавливать вид функ­циональной зависимости между величинами на основании анализа размерностей, с учетом того, что произведение величин с основа­ниями даже разных размерностей и рациональными показателями степеней может иметь физический смысл, тогда как сумма или разность величин неодинаковых размерностей смысла не имеет.

Дата добавления: 2015-04-24