О сущности метода

Сущность метода Монте-Карло состоит в том, что искомая величина представляется в виде математического ожидания неко­торой случайной величины, математическое ожидание которой за­меняется средним арифметическим реализаций этой случайной ве­личины при большом числе испытаний, обычно проводимых на ЭВМ. При этом оценка погрешности метода сводится к интер­вальной оценке погрешности математического ожидания.

Особенностью метода является простая структура вычисли­тельного алгоритма, в соответствии с которым составляется про­грамма для проведения одного испытания, которое затем много­кратно повторяется. Именно поэтому метод Монте-Карло называ­ют еще и методом статистических испытаний.

6) 1. ПРОИЗВОДНАЯ КАК МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ФИЗИЧЕСКИХ, ТЕХНИЧЕСКИХ И ЭКОНОМИЧЕСКИХ ПОНЯТИЙ И ВЕЛИЧИН, ИХ ЗАВИСИМОСТЕЙ.

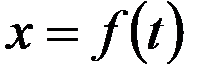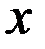Рассмотрим общую задачу об определении мгновенной скорости движения точки, абсцисса которой есть функция времени: . Итак, в момент времени абсцисса точки равна 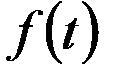, в момент времени 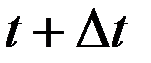её абсцисса будет 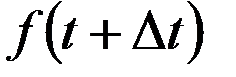, поэтому приращение абсциссы точки равно

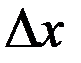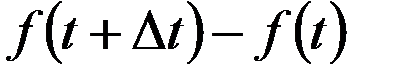= и .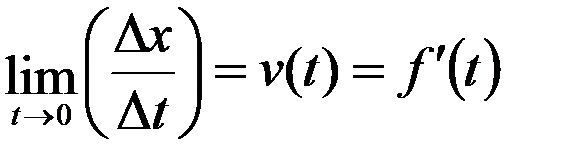

Следовательно, первая производная от абсциссы движущейся точки по времени есть скорость (проекция скорости на ось 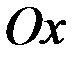– физический смысл производной), а вторая – т.е. 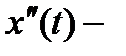проекция ускорения на ту же ось (физический смысл второй производной).

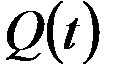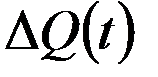Аналогично, если – объём продукции, выпускаемой за время , то часть продукции , выпущенной за промежуток времени 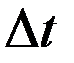и отнесённая к 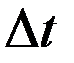, может быть истолкована как средняя производительность 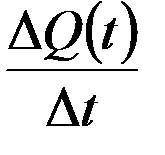, а тогда под производительностью 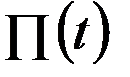в данный момент времени естественно понимать производную 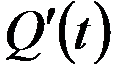, т.е. 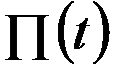= 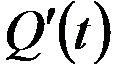(Экономический смысл производной).

Рисунок 11.2 – Модель стержня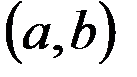

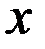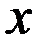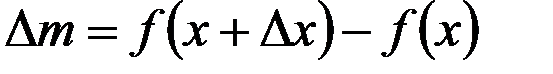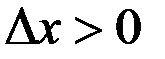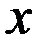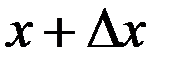Теперь рассмотрим задачу об определении плотности стержня в точке. Для этого (рисунок 11.2) левый конец стержня совместим с точкой а, правый – с точкой b и обозначим через абсциссу какой – либо точки этого стержня. Масса части стержня, расположенного левее точки , есть неубывающая функция и приращение , где равно массе участка стержня между точками и , а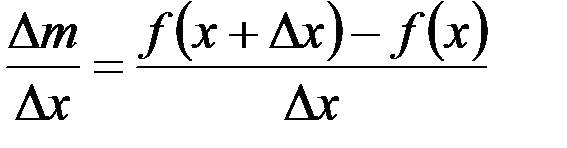

есть средняя плотность распределения массы стержня на участке длиною 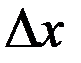. Переходя к пределу в последнем равенстве при 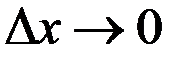, найдём плотность стержня в точке :

,

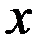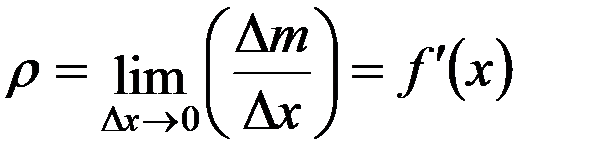конечно при условии, что этот предел существует.

Решения приведённых задач по существу сводились к одной и той же операции: нахождению предела приращения функции к приращению аргумента, когда последнее стремится к нулю. Существует очень много прикладных и научных задач, результатом решения которых является указанный предел. Отвлекаясь от физического смысла участвующих в таких задачах величин, мы приходим к единству таких математических моделей, к математической модели, общей для всех таких задач. В рассматриваемом случае такой моделью является производная.

6) 2. ЭКОНОМИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ПРОИЗВЕДЕНИЯ МАТРИЦЫ-СТРОКИ НА МАТРИЦУ-СТОЛБЕЦ.

В экономике и других областях часто приходится иметь дело с прямоугольными таблицами, которым соответствуют такие математические модели как матрицы. В частности, каждый вектор можно рассматривать как матрицу, состоящую из одной строки и ли одного столбца, т.е. матрица является обобщением такого понятия как n мерный вектор. Именно поэтому матрице и операциям над матрицами можно дать экономическую интерпретацию, обобщающую аналогичную для n мерных векторов.

Итак, пусть k фабрик выпускают n различных видов продукции каждая. Тогда отчет о производстве за год всех k фабрик может быть описан с помощью матрицы (таблицы)

где a_ij - количество продукции j - го вида выпущенной i -й фабрикой за год. Выпуск

продукции, например, за 1, 2 года при сохранении производительности будет характеризоваться матрицей

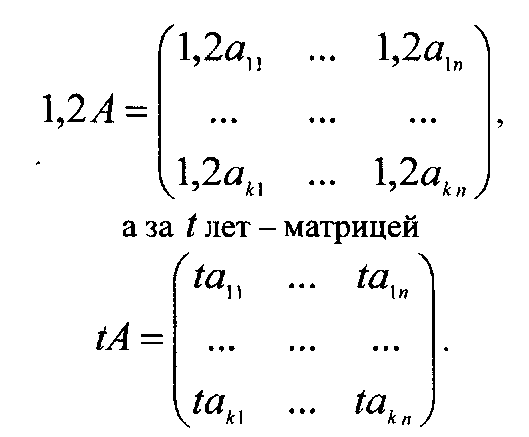
Выпуск тех же n видов продукции другой группой из к фабрик, специализирующихся соответственно на той же продукции, будет характеризоваться второй матрицей В с элементами b_ij а совокупный продукт обеих групп фабрик может быть описан

матрицей А + В с элементами а_ij + b_ij.

Теперь укажем экономический смысл произведения матрицы строки на матрицу столбец, рассматривая множители как векторы, а результат - как скалярное произведение.

Тогда, учитывая обозначения компонентов векторов - ā и 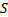, можем написать равенство, в правой части которого получится величина, равная стоимости годового объема продукции фабрики. Отметим, что «скалярное» произведение «строки» на «столбец» дает «квадратную» матрицу первого порядка, т.е. число:

7) 1. ДВЕ СХЕМЫ ПРИЛОЖЕНИЯ ИНТЕГРАЛА К ПОСТРОЕНИЮ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ.

Первая основана на определении определенного интеграла как предела интегральной суммы. При этом искомая величина приближенно представляется в виде интегральной суммы с последующим предельным переходом как при вычислении площади криволинейной трапеции.

При применении второй схемы предполагается существование такой дифференцируемой функции, на основании которой определяется искомая величина, для чего из условия задачи находится дифференциал (или производная) этой функции и вычислением определенного интеграла получается значение искомой величины. Подчеркнем, что в этой схеме сначала выдвигается гипотеза о существовании указанной функции, однако эта нестрогость не имеет значения, так как в каждой конкретной задаче мы эту функцию фактически находим и тем самым убеждаемся в справедливости выдвинутой гипотезы.

Задача 1

а) Определить работу, необходимую для запуска ракеты весом Р с поверхности земли на высоту Н.

b) Определить работу, которую должен совершить двигатель, чтобы полностью освободить ракету от земного притяжения.

При решении землю и ракету примем за материальные точки с соответствующими массами. По закону всемирного тяготения 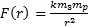, где k – коэффициент пропорциональности, 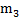-масса земли, 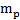-масса ракеты, r-расстояние между материальными точками, моделирующими землю и ракету. Так как на поверхности земли радиуса R (рисунок1) r=R и F=P, то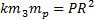 . Обозначим через A(r) работу, которую совершает двигатель ракеты при r>R, тогда dA=F(r)dr и работа на пути от r=R r=R+H будет равна

A= 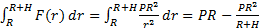(1)

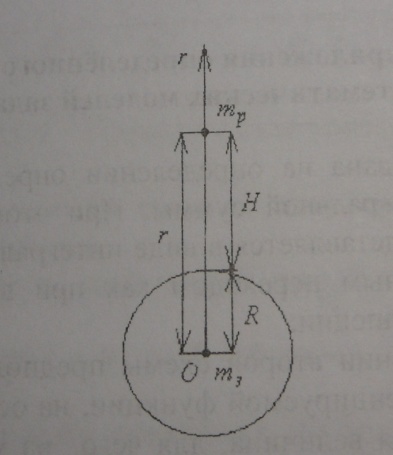
Рисунок - Модель сечения Земли

Теперь ясно, что для определения работы, которую должен совершить двигатель, чтобы полностью освободить ракету от земного притяжения, необходимо в интеграле (1) перейти к пределу 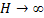, тогда получим

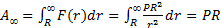(2)

Итак, работа оказалась конечной величиной, а несобственный интеграл с бесконечным пределом здесь представляет математическую модель, адекватно отражающую объективную действительность.

Задача 2

Тело массой m совершает вдоль прямой горизонтальные колебания под действием пружины (рисунок пружинный маятник). Найти период колебаний этого тела, пренебрегая массой пружины, трением и сопротивлением среды.

Решение: ось x направим вдоль прямой колебаний, а начало координат поместим в точке равновесия (рисунок).

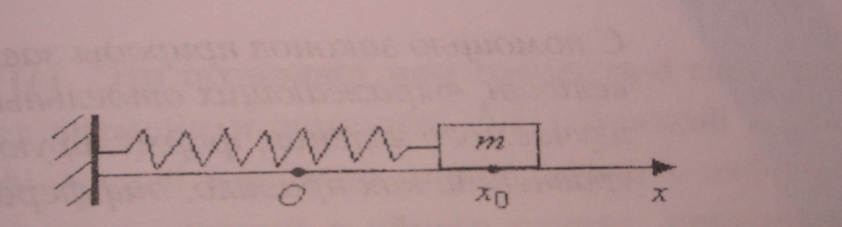
Рисунок – Пружинный маятник

Для определения периода колебаний отклоним материальную точку (модель тела) m вправо на расстояние x₀ и отпустим при v=0. Поскольку dx=vdt, период колебаний будет

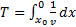(1)

Сейчас для нас важно, что знаменатель v подынтегральный функции при x₌x₀ равен нулю, т.е. правая часть, является несобственным интегралом от неограниченной функции, но этот интеграл представляет собой математическую модель реальной величины-периода колебаний. Проще всего найти этот интеграл, используя физический закон сохранения энергии

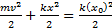, из которого имеем:

,

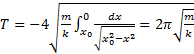
здесь перед корнем поставлен знак минус, так как v<0 при 0< x<x₀ (проекция скорости на ось x – отрицательная, поскольку точка движется влево).

Дата добавления: 2015-04-24