Определенный интеграл как Математическая модель

Задача, приводящая к понятию интеграла

Задача об определении площади криволинейной трапеции

Так называют плоскую фигуру (рисунок 12.1), ограниченную графиком непрерывной на отрезке 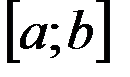функции 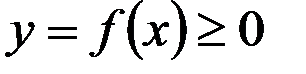, отрезком 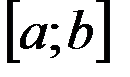и прямым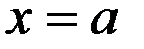и и 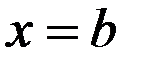. При определении её площади, буем исходить из простейшей фигуры – прямоугольника, площадь которого легко вычисляется. Для решения задачи разобьём отрезок 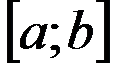на 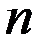равных частичных отрезков точками 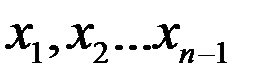, и положим для общности , 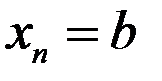(рисунок 12.1) и на каждом из них построим прямоугольник с высотой, равной ординате в середине частичного отрезка: 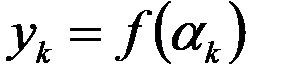, 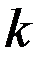– номер частичного отрезка. Поэтому площадь

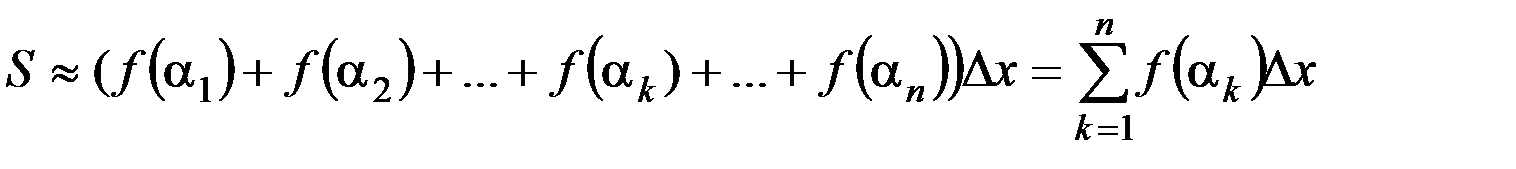(12.1)

где

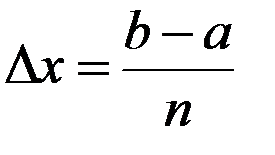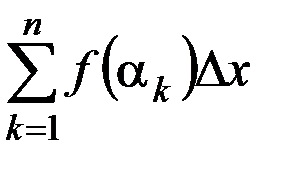, – интегральная сумма.

При

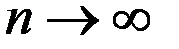, S =

(геометрический смысл определённого интеграла). Формула (12.1) может быть применена и для приближённого вычисления площади криволинейной трапеции и определённого интеграла.

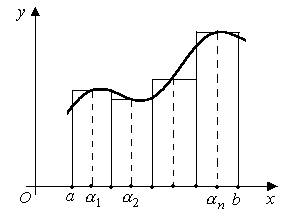
Рисунок 12.1 – Криволинейная трапеция

Две схемы приложения определённого интеграла к построению математических моделей задач

Первая основана на определении определённого интеграла как предела интегральной суммы. При этом искомая величина приближённо представляется в виде интегральной суммы с последующим предельным переходом как при вычислении площади криволинейной трапеции.

При применении второй схемы предполагается существование такой дифференцируемой функции, на основании которой определяется искомая величина, для чего из условия задачи находится дифференциал (или производная) этой функции и вычислением определённого интеграла получается значение искомой величины. Подчеркнём, что в этой схеме сначала выдвигается гипотеза о существовании указанной функции, однако эта нестрогость не имеет значения, так как в каждой конкретной задаче мы эту функцию фактически находим и тем самым убеждаемся в справедливости выдвинутой гипотезы.

Дата добавления: 2015-04-24