
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доказательство теоремы. Ответы на тесты по Технологическому оборудованию
|
|
|
|
Замечание
Ответы на тесты по Технологическому оборудованию
| № задания | ответ |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | |
| 6. | |
| 7. | |
| 8. | |
| 9. | |
| 10. | |
| 11. | |
| 12. | |
| 13. | |
| 14. | |
| 15. | |
| 16. | |
| 17. | |
| 18. | |
| 19. | |
| 20. | |
| 21. | |
| 22. | |
| 23. | |
| 24. | |
| 25. | |
| 26. | |
| 27. | |
| 28. | |
| 29. | |
| 30. | |
| 31. | |
| 32. | |
| 33. | |
| 34. | |
| 35. | |
| 36. | |
| 37. | |
| 38. | |
| 39. | |
| 40. | |
| 41. | |
| 42. | |
| 43. | |
| 44. | |
| 45. | |
| 46. | |
| 47. | |
| 48. | |
| 49. | |
| 50. | |
| 51. | |
| 52. | |
| 53. | |
| 54. | |
| 55. | |
| 56. | |
| 57. | |
| 58. | |
| 59. | |
| 60. |
В теореме можно поменять ролями x и y, т.е. можно предположить, что выполнены следующие два условия:
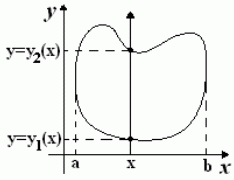
1) область D такова, что любая прямая, параллельная оси Ох, пересекает границу Г по целому отрезку 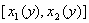 либо не более чем в двух точках, ординаты которых есть
либо не более чем в двух точках, ординаты которых есть 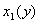 и
и 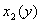 , где
, где  ;
;
2) функция 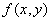 интегрируема в области D и для любого
интегрируема в области D и для любого 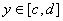 допускает существование однократного интеграла
допускает существование однократного интеграла  (
(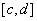 - проекция области D на ось Оy). Тогда существует повторный интеграл
- проекция области D на ось Оy). Тогда существует повторный интеграл 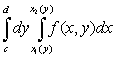 и справедливо равенство
и справедливо равенство 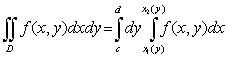 .
.
Если область D можно записать неравенствами:
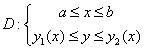 , то
, то 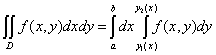 ,
,
 .
.
Справа стоит повторный интеграл, в котором внутренний интеграл вычисляется по переменной y в предположении, что x = const; результатом вычисления внутреннего интеграла является некоторая функция Ф(x). Затем вычисляется внешний интеграл от Ф(x) по переменной x в постоянных пределах; в результате получается число.
Вывод формулы:

Т.к. 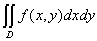 не зависит от способа разбиения области D на части, то сделаем разбиение горизонтальными и вертикальными прямыми на прямоугольные элементарные части. Всего элементарных частей будет:
не зависит от способа разбиения области D на части, то сделаем разбиение горизонтальными и вертикальными прямыми на прямоугольные элементарные части. Всего элементарных частей будет: 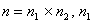 , n1 - количество частей по оси OX, n2 - количество частей по оси OY.
, n1 - количество частей по оси OX, n2 - количество частей по оси OY. 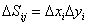 - площадь элементарной части.
- площадь элементарной части.
|
|
|
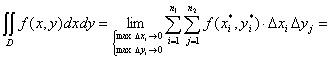
{выполним суммирование сначала по j, т.е. по вертикальным элементарным частям при фиксированном 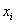 , затем по i, т.е. просуммируем массы вертикальных полосок}
, затем по i, т.е. просуммируем массы вертикальных полосок}
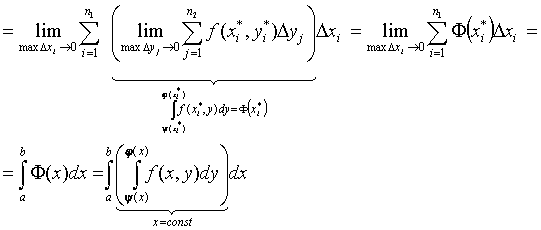 (1)
(1)
Здесь 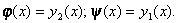
Смысл формулы (1) можно также проиллюстрировать на объеме цилиндроида, зная формулу для вычисления объема тела с известной площадью поперечного сечения:
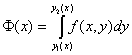 - площадь поперечного сечения,
- площадь поперечного сечения,
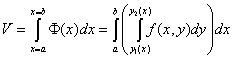
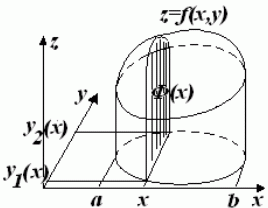
Теорема 1. Пусть область V ограничена снизу и сверху поверхностями 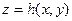 и
и 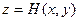 , где
, где 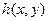 и
и 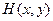 - непрерывные функции в замкнутой области
- непрерывные функции в замкнутой области 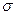 плоскости XOY, и цилиндрической поверхностью, у которой образующие параллельны оси Oz, а направляющей является граница области
плоскости XOY, и цилиндрической поверхностью, у которой образующие параллельны оси Oz, а направляющей является граница области 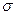 . Тогда для любой функции
. Тогда для любой функции  , непрерывной в замкнутой области V, имеет место формула
, непрерывной в замкнутой области V, имеет место формула
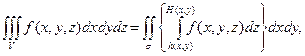 (1)
(1)
позволяющая свести вычисление тройного интеграл к вычислению двойного интеграла от определенного интеграла (короче, к вычислению повторного интеграла).
Интеграл, стоящий в правой части равенства, обычно записывают в виде:
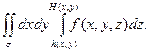
При вычислении тройного интеграла по формуле (1) с помощью повторного интеграла сначала вычисляют внутренний интеграл по переменной z при постоянных x и y (x и y – параметры) в пределах изменения z (для области V) при постоянных x и y, а затем полученная функция x и y интегрируется по переменным x и y по области 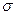 .
.
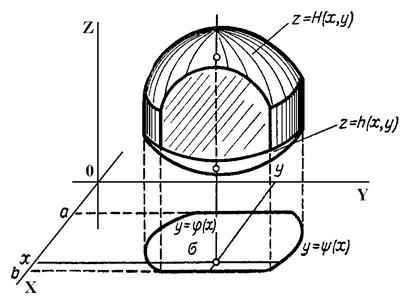
Рис. 4.13.1
Если при этом область 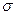 плоскости XOY ограничена линиями x = a, y = b (a < b),
плоскости XOY ограничена линиями x = a, y = b (a < b), 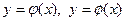 [
[ 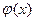 и
и 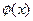 непрерывные на отрезке [а, b] функции, причем
непрерывные на отрезке [а, b] функции, причем 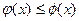 (рис. 4.13.1.)], то, перейдя от двойного интеграла по области
(рис. 4.13.1.)], то, перейдя от двойного интеграла по области 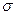 к повторному, получаем формулу
к повторному, получаем формулу
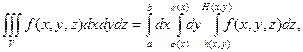 (2)
(2)
позволяющую вычисление тройного интеграла заменить последовательным вычислением трех определенных интегралов.
В частности, если область V – параллелепипед с гранями x = a, x = b (a < b), y = c, y = d (c < d), z = l, z = k (l < k), то по формуле (2) имеем:
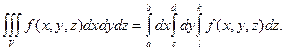
Для функции  , равной произведению функций, каждая из которых зависит от одного лишь переменного:
, равной произведению функций, каждая из которых зависит от одного лишь переменного:
|
|
|
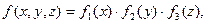
тройной интеграл по этому параллелепипеду V равен произведению трех определенных интегралов:
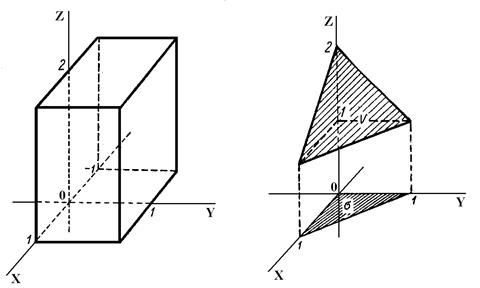
Рис. 4.13.2 Рис. 4.13.3
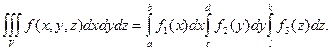
Это равенство непосредственно следует из свойств тройных и двойных интегралов.
- Цилиндрическая система координат.
Цилиндрические координаты точки Р(ρ,φ,z) – это полярные координаты ρ, φ проекции этой точки на плоскость Оху и аппликата данной точки z (рис.2).
Формулы перехода от цилиндрических координат к декартовым можно задать следующим образом:
x = ρ cosφ, y = ρ sinφ, z = z. (9.4)
- Сферическая система координат.
В сферических координатах положение точки в пространстве определяется линейной координатой ρ – расстоянием от точки до начала декартовой системы координат (или полюса сферической системы), φ – полярным углом между положительной полуосью Ох и проекцией точки на плоскость Оху, и θ – углом между положительной полуосью оси Оz и отрезком OP (рис.3). При этом
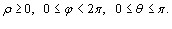
Зададим формулы перехода от сферических координат к декартовым:
x = ρ sinθ cosφ, y = ρ sinθ sinφ, z = ρ cosθ. (9.5)
Якобиан и его геометрический смысл.
Рассмотрим общий случай замены переменных в двойном интеграле. Пусть в плоскости Оху дана область D, ограниченная линией L. Предположим, что х и у являются однозначными и непрерывно дифференцируемыми функциями новых переменных u и v:
x = φ(u, v), y = ψ(u, v). (9.6)
Рассмотрим прямоугольную систему координат Оuv, точка Р΄(u, v) которой соответствует точке Р(х, у) из области D. Все такие точки образуют в плоскости Оuv область D΄, ограниченную линией L΄. Можно сказать, что формулы (9.6) устанавливают взаимно однозначное соответствие между точками областей D и D΄. При этом линиям u = const и
v = const в плоскости Оuv будут соответствовать некоторые линии в плоскости Оху.
Рассмотрим в плоскости Оuv прямоугольную площадку ΔS΄, ограниченную прямыми u = const, u+Δu = const, v = const и v+Δv = const. Ей будет соответствовать криволинейная площадка ΔS в плоскости Оху (рис.4). Площади рассматриваемых площадок тоже будем обозначать ΔS΄ и ΔS. При этом ΔS΄ = Δu Δv. Найдем площадь ΔS. Обозначим вершины этого криволинейного четырехугольника Р1, Р2, Р3, Р4, где
P1(x1, y1), x1 = φ(u, v), y1 = ψ(u, v);
|
|
|
P2(x2, y2), x2 = φ(u+Δu, v), y2 = ψ(u+Δu, v);
P3(x3, y3), x3 = φ(u+Δu, v+Δv), y3 = ψ(u+Δu, v+Δv);
P4(x4, y4), x4 = φ(u, v+Δv), y4 = ψ(u, v+Δv).
Заменим малые приращения Δu и Δv соответствующими дифференциалами. Тогда
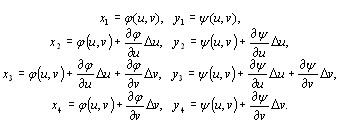
При этом четырехугольник Р1 Р2 Р3 Р4 можно считать параллелограммом и определить его площадь по формуле из аналитической геометрии:
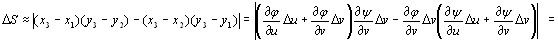
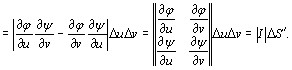 (9.7)
(9.7)
Определение 9.3. Определитель 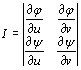 называется функциональным определителем или якобианом функций φ(х, у) и ψ(х, у).
называется функциональным определителем или якобианом функций φ(х, у) и ψ(х, у).
Переходя к пределу при 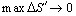 в равенстве (9.7), получим геометрический смысл якобиана:
в равенстве (9.7), получим геометрический смысл якобиана:
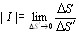 , (9.8)
, (9.8)
то есть модуль якобиана есть предел отношения площадей бесконечно малых площадок ΔS и ΔS΄.
Замечание. Аналогичным образом можно определить понятие якобиана и его геометрический смысл для п-мерного пространства: если x1 = φ1(u1, u2,…,un), x2 = φ2(u1, u2,…,un),…, xn = φ(u1, u2,…, un), то
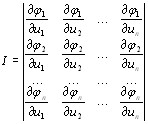 (9.8)
(9.8)
При этом модуль якобиана дает предел отношения «объемов» малых областей пространств х1, х2,…, хп и u1, u2,…, un.
Замена переменных в кратных интегралах.
Исследуем общий случай замены переменных на примере двойного интеграла.
Пусть в области D задана непрерывная функция z = f(x,y), каждому значению которой соответствует то же самое значение функции z = F(u, v) в области D΄, где
F(u, v) = f(φ(u, v), ψ(u, v)). (9.9)
Рассмотрим интегральную сумму
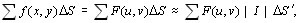
где интегральная сумма справа берется по области D΄. Переходя к пределу при 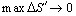 , получим формулу преобразования координат в двойном интеграле:
, получим формулу преобразования координат в двойном интеграле:
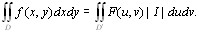 (9.10)
(9.10)
Аналогичным образом можно вывести подобную формулу для тройного интеграла:
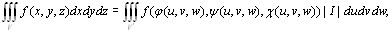 (9.11)
(9.11)
где x = φ(u, v, w), y = ψ(u, v, w), z = χ(u, v, w),
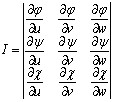 , (9.12)
, (9.12)
а область V пространства Оxyz отображается в область V΄ пространства Ouvw.
Переход к цилиндрическим и сферическим координатам
в тройном интеграле.
Найдем, используя формулы (9.4), (9.5) и (9.12), якобианы перехода от декартовых координат к цилиндрическим и сферическим:
- для цилиндрических координат
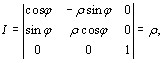 (9.13)
(9.13)
- для сферических координат
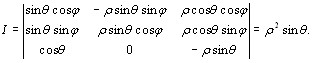 (9.14)
(9.14)
Тогда формулы перехода к цилиндрическим или сферическим координатам в тройном интеграле будут выглядеть так: (9.15)
|
|
|
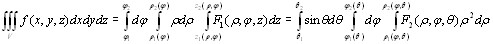 ,
,
где смысл обозначений понятен из предыдущего текста.
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 486; Нарушение авторских прав?; Мы поможем в написании вашей работы!