
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные понятия математической статистики 2 страница
|
|
|
|
Проверяемая гипотеза называется нулевой и обозначается 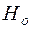 . Альтернативная гипотеза, которая обозначается
. Альтернативная гипотеза, которая обозначается  , принимается в случае не принятия нулевой гипотезы. Однако если отвергается нулевая гипотеза, может быть принято решение об уточнении данных, а не о принятии альтернативной гипотезы
, принимается в случае не принятия нулевой гипотезы. Однако если отвергается нулевая гипотеза, может быть принято решение об уточнении данных, а не о принятии альтернативной гипотезы  .
.
По выборке 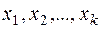 из генеральной совокупности необходимо принять или отвергнуть гипотезу
из генеральной совокупности необходимо принять или отвергнуть гипотезу 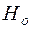 . С этой целью строится статистика,
. С этой целью строится статистика, 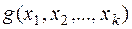 , которая имеет функцию распределения
, которая имеет функцию распределения 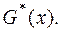 Область определения этой функции разбивается на две области:
Область определения этой функции разбивается на две области: 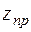 (правильная) и
(правильная) и 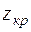 (критическая). Если
(критическая). Если  , то принимается
, то принимается 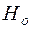 ; если
; если  , то принимается
, то принимается  .
. 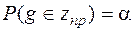 .
.
При любом результате проверки гипотезы есть вероятность допустить ошибку. Если отклоняется верная гипотеза, то совершается ошибка первого рода. Если принимается ложная гипотеза, то совершается ошибка второго рода.
Вероятность α совершить ошибку первого рода называется уровнем значимости гипотезы. Этот уровень (вероятность отклонить верную гипотезу) выбирают как можно меньше (0,01; 0,05…) в том случае, если ошибка первого рода влечёт большие потери, а ошибка второго рода – малые. Единственный способ одновременного уменьшения вероятностей этих ошибок – это увеличение объёма выборки.
Пусть гипотеза состоит в том, что генеральная совокупность подчиняется некоторому закону распределения. По выборке нужно подтвердить или опровергнуть эту гипотезу. Критерий для проверки такой гипотезы называется критерием согласия.
При решении социологических задач модель закона распределения в общем случае неизвестна, поэтому возникает необходимость выбора закона распределения, согласующегося с результатами выборочных наблюдений. В предлагаемом задании следует рассмотреть критерий Пирсона, схема проверки которого состоит в следующем:
|
|
|
1. По выборочным данным проводят оценку параметров выбранной модели закона распределения. Предполагают, что закон распределения имеет r параметров.
2. Подставляя выборочные оценки значений параметров распределения, находят теоретические значения вероятностей:
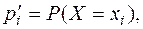 i =1, 2, … k. (27)
i =1, 2, … k. (27)
3. Рассчитывают теоретические частоты:
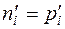
 где
где 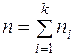 (28)
(28)
4. Рассчитывают значение критерия согласия Пирсона:
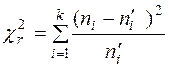 (29)
(29)
Эта величина при n  стремится к распределению
стремится к распределению 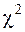 с l=k-r -1 степенями свободы. Поэтому для расcчётов используют таблицы распределения
с l=k-r -1 степенями свободы. Поэтому для расcчётов используют таблицы распределения 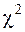 (Приложение 6).
(Приложение 6).
5. Задаваясь достаточно малой вероятностью (уровнем значимости 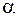 ), находят критическую область (она всегда правосторонняя) ((
), находят критическую область (она всегда правосторонняя) ((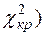 ;
;  ; значение (
; значение (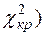 определяют из соотношения
определяют из соотношения 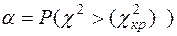 . Если численное значение
. Если численное значение 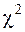 попадает в интервал ((
попадает в интервал ((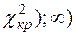 , то гипотеза
, то гипотеза 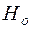 : F(x)=
: F(x)= 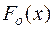 отклоняется и принимается альтернативная гипотеза о том, что выбранная модель закона распределения не подтверждается выборочными данными, при этом допускается ошибка, вероятность которой равна α.
отклоняется и принимается альтернативная гипотеза о том, что выбранная модель закона распределения не подтверждается выборочными данными, при этом допускается ошибка, вероятность которой равна α.
Элементы теории корреляции
Многие социологические задачи требуют установить и оценить зависимость двух и более случайных величин. Эта зависимость может быть функциональной, статистической или совсем отсутствовать.
Отсутствие зависимости (связи) характерно для независимых случайных величин.
Если каждому значению случайной величины X соответствует определённое значение случайной величины Y, то говорят, что X и Y имеют между собой функциональную зависимость. Эта зависимость реализуется редко, так как обе величины подвержены действию случайных факторов.
Если каждому значению случайной величины X соответствует вполне определённый закон распределения случайной величины Y, то говорят, что X и Y имеют статистическую зависимость. Частным случаем такой зависимости является корреляционная зависимость, когда при изменении одной из величин изменяется среднее значение другой.
|
|
|
Для исследования влияния одной величины на изменение другой рассматривают условные законы распределения первой величины при фиксированных значениях второй. Пусть Х получила одно из своих значений 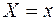 ; при этом другая величина Y может принять любое из возможных значений
; при этом другая величина Y может принять любое из возможных значений 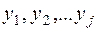 . Среднюю арифметическую значений Y, соответствующих значению
. Среднюю арифметическую значений Y, соответствующих значению 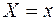 называют условной средней
называют условной средней  .
.
Корреляционной зависимостью Y от X называют функциональную зависимость условной средней  от x, а выражение (30) уравнением регрессии Y на X, её график – линией регрессии Y на X.
от x, а выражение (30) уравнением регрессии Y на X, её график – линией регрессии Y на X.
 =f(x) (30)
=f(x) (30)
Аналогично определяется условная средняя 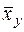 , и корреляционная зависимость Х от Y.
, и корреляционная зависимость Х от Y.
Выражение (31) называют уравнением регрессии Х на Y, а функцию 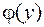 - регрессией Х на Y, её график – линией регрессии Х на Y.
- регрессией Х на Y, её график – линией регрессии Х на Y.
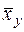 =
= 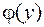 (31)
(31)
Задача теории корреляции состоит в определении формы корреляционной зависимости и оценки тесноты этой зависимости. Функция регрессии может быть линейной, квадратичной, показательной и т. д. Если функции (30), (31) линейные, то корреляционная зависимость называется линейной, в противном случае – нелинейной.
Степень зависимости Y от X оценивается по величине рассеяния значений Y вокруг условного среднего  . Большое рассеяние свидетельствует о слабой зависимости, либо об её отсутствии, малое – указывает на не достаточно сильную зависимость.
. Большое рассеяние свидетельствует о слабой зависимости, либо об её отсутствии, малое – указывает на не достаточно сильную зависимость.
Для того, чтобы иметь конкретное представление о двумерном распределении и его характеристиках, результаты n наблюдений, в каждом из которых регистрируются совместные значения X и Y, вносят в корреляционную таблицу (таблица 7).
Если одна и та же пара чисел (x,y) наблюдается несколько раз, то эти данные группируют, т.е. подсчитывают частоты  .
.
В первой строке таблицы указывают наблюдаемые значения признака Х, а в первом столбце – наблюдаемые значения признака Y. На пересечении строк и столбцов вписывают частоты 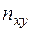 наблюдаемых пар значений признаков. В последнем столбце записывают суммы частот строк, а в последней строке – суммы частот столбцов. В клетке, расположенной в нижнем правом углу таблицы, помещают сумму всех частот, т.е. общее число всех наблюдений.
наблюдаемых пар значений признаков. В последнем столбце записывают суммы частот строк, а в последней строке – суммы частот столбцов. В клетке, расположенной в нижнем правом углу таблицы, помещают сумму всех частот, т.е. общее число всех наблюдений.
Выборочное уравнение линейной регрессии Y на X имеет вид:
|
|
|
 (32)
(32)
Так как по выборочным данным можно получить только оценки параметров, то оценку коэффициента k обозначим через 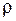 , а оценку b через
, а оценку b через 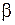 , т.е.
, т.е.
 =
= 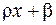 (33)
(33)
Используя метод наименьших квадратов, основанный на минимизации суммы квадратов отклонений теоретических значений функции от наблюдаемых значений 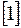 , получим формулы для отыскания
, получим формулы для отыскания 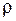 и
и 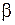 .
.
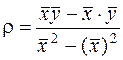 , (34)
, (34)
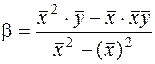 , (35)
, (35)
где 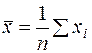 , (36)
, (36)
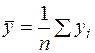 , (37)
, (37)
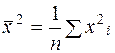 , (38)
, (38)
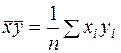 . (39)
. (39)
Однако чаще уравнение регрессии записывают в другом виде с использованием выборочного коэффициента корреляции. Для этого находят 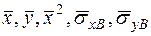 ,
,  :
:
 , (40)
, (40)
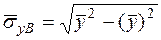 , (41)
, (41)
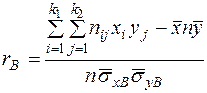 , (42)
, (42)
где 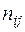 - частота пары (
- частота пары (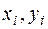 ).
).
Затем получают выборочное уравнение линейной регрессии Y на X в виде:
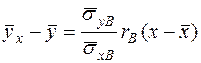 (43)
(43)
или выборочное уравнение линейной регрессии X на Y в виде:
 . (44)
. (44)
Коэффициент корреляции служит для оценки тесноты линейной корреляционной зависимости. Отметим свойства коэффициента 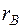 :
:
1. 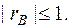
2. Если X и Y независимы, то  . Если
. Если  , то X и Y – некоррелированы.
, то X и Y – некоррелированы.
3. При | 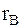 |=1 зависимость становится линейной.
|=1 зависимость становится линейной.
Для получения выводов о практической значимости математической модели, показаниям тесноты связи даётся качественная оценка. Это осуществляется на основе шкалы Чеддока: если 0,1< 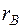 <0,3 – связь слабая, если 0,3<
<0,3 – связь слабая, если 0,3< 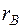 <0,5 – связь умеренная, если 0,5<
<0,5 – связь умеренная, если 0,5< 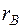 <0,7 – связь заметная, если 0,7<
<0,7 – связь заметная, если 0,7< 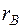 <0,9 – связь высокая, если 0,9<
<0,9 – связь высокая, если 0,9< 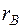 <0,99 – связь весьма высокая.
<0,99 – связь весьма высокая.
В случае нелинейной корреляции 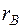 утрачивает своё значение, как мера связи.
утрачивает своё значение, как мера связи.
Может оказаться, что для некоторой таблицы распределения 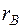 =0, в то время как между величинами имеется несомненная зависимость. Для измерения степени зависимости в случае нелинейной корреляции между случайными величинами применяется корреляционное отношение:
=0, в то время как между величинами имеется несомненная зависимость. Для измерения степени зависимости в случае нелинейной корреляции между случайными величинами применяется корреляционное отношение:
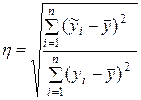 , (45)
, (45)
где 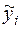 - выровненные точки регрессии.
- выровненные точки регрессии.
Корреляционное отношение имеет следующие свойства:
1. 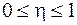 .
.
2. Если  =0, то признак Y с признаком X корреляционной зависимостью не связан.
=0, то признак Y с признаком X корреляционной зависимостью не связан.
3. Если  =1, то признак Y связан с признаком X функциональной зависимостью.
=1, то признак Y связан с признаком X функциональной зависимостью.
4. Если 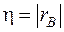 , имеет место точная линейная корреляционная зависимость.
, имеет место точная линейная корреляционная зависимость.
5. Во всех других случаях 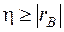 .
.
Для оценки адекватности уравнения регрессии может использоваться показатель средней ошибки аппроксимации:
|
|
|
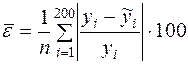 %, (46)
%, (46)
где  - линейные отклонения абсолютных величин эмпирических и выровненных точек регрессии.
- линейные отклонения абсолютных величин эмпирических и выровненных точек регрессии.
При 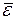 <10% модель является достаточно адекватной реальной зависимости величины Y от X.
<10% модель является достаточно адекватной реальной зависимости величины Y от X.
При численности объектов анализа n<30 возникает необходимость определения точности и значимости параметров 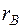 ,
,  ,
,  .
.
Для оценки значимости 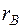 применяется t-критерий Стьюдента. При этом определяется фактическое значение критерия:
применяется t-критерий Стьюдента. При этом определяется фактическое значение критерия:
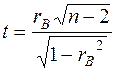 (47)
(47)
Вычисленное значение t сравнивается с критическим, которое берётся из таблицы значений t-Стьюдента с учётом заданного уровня значимости и числа степеней свободы k.
Если t>  , то величина
, то величина 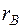 признаётся существенной.
признаётся существенной.
Для оценки значимости параметров  и
и  сначала определяют среднее квадратическое отклонение результирующего признака
сначала определяют среднее квадратическое отклонение результирующего признака 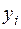 от выровненных значений
от выровненных значений 
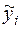 :
:
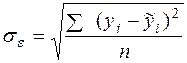 (48)
(48)
Затем вычисляют среднее квадратическое отклонение факторного признака 
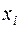 от общей средней
от общей средней 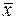 :
:
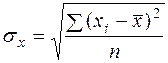 (49)
(49)
При этом фактические значения t-критерия:
для параметра  :
:
 (50)
(50)
для параметра  :
:
 (51)
(51)
Полученные по формулам фактические значения 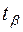 и
и  сравниваются с критическим
сравниваются с критическим  . Полученные в анализе корреляционной зависимости параметры уравнения регрессии признаются типичными, если t фактическое больше t критического:
. Полученные в анализе корреляционной зависимости параметры уравнения регрессии признаются типичными, если t фактическое больше t критического:
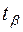 >
>  <
<  (52)
(52)
Далее находят доверительные интервалы для коэффициентов  и
и  :
:
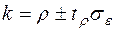 (53)
(53)
 , (54)
, (54)
где 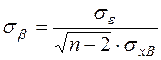 (55)
(55)
При вычислении прогнозного значения необходимо получить оценку его точности. При заданных значениях надёжности 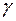 , степени свободы
, степени свободы  k и найденному
k и найденному 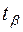 получим:
получим:
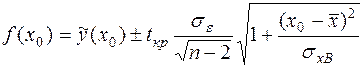 (56)
(56)
В заключении необходимо отметить, что на основе проделанного корреляционного анализа делаются выводы о пригодности математической модели и её практическом использовании.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 456; Нарушение авторских прав?; Мы поможем в написании вашей работы!