Смешанные стратегии

В приведенных примерах описаны ситуации, в которых интересы игроков не совпадают. Естественно встает вопрос о том, какие рекомендации не­обходимо дать игрокам для того, чтобы моделируемая конфликтная ситуация разрешилась.

Иными словами, что мы будем понимать под решением биматричной игры?

Попробуем ответить на этот вопрос так: вследствие того, что ин­тересы игроков не совпадают, нам нужно построить такое (компромиссное) решение, которое бы в том или ином, но в одинаковом смы­сле удовлетворяло обоих игроков.

Иначе говоря, попробуем найти некую равновесную ситуацию, яв­ное отклонение от которой уменьшает выигрыш игрока.

Подобный вопрос мы ставили и при рассмотрении матричных игр. Напомним, что возникавшее при разработке минимаксного подхода понятие равновесной ситуации приводило нас к поиску седловой точки, которая, как оказалось, существует далеко не всегда.

Естественно ожидать, что в более сложном случае биматричной игры дело вряд ли будет обстоять проще.

В матричных играх эта трудность была преодолена путем перехода к смешанным стратегиям, т. е. к такому поведению игроков, при котором они чередуют свои собственные чистые стратегии.

Иными словами, любая матричная игра в смешанных стратегиях разрешима.

Поэтому, рассматривая здесь биматричные игры, разумно попробовать сразу же перейти к смешанным стратегиям игроков. Тем самым мы предполагаем, что каждая игра может быть повторена в неизменных обстоятельствах многократно.

2 ´ 2 - биматричные игры. Ситуация равновесия

В 2´2 - биматричной игре платежные матрицы игроков имеют следующий вид:

А= 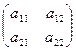, В= .

Вероятности выбора стратегий игрока А р ₁ =р, р ₂=1 – р, игрока В q ₁ =q, q ₂=1– q, а средние выигрыши вычисляются по формулам

H_A(р, q) = a ₁₁ pq + a ₁₂ p (l - q) + a ₂₁(l - p) q + a ₂₂(1 - p)(l - q),

H_B(р, q) = b ₁₁ pq + b ₁₂ p (l - q) + b ₂₁(l - p) q + b ₂₂(1 - p)(l - q),

где

0 £ р £ 1, 0 £ q £ l.

Определение. Будем говорить, что пара чисел

(p*, q *), 0 £ р* £ 1, 0 £ q* £ l,

определяет равновесную ситуацию, если для любых р и q, подчиненных условиям 0 £ р £ 1, 0 £ q £ l, одновременно выполнены следующие неравенства:

H_A(р, q*) £ H_A(р*, q*), H_B(р*, q) £ H_B(р *, q *). (2.7.3)

Пояснение. Неравенства (2.7.3)означают следующее: ситуация, определяемая смешанной стратегией (р *, q *), является равновесной, если отклонение от нее одного из игроков при условии, что другой сохраняет свой выбор, приводит к уменьшению выигрыша первого. Тем самым получается, что если равновесная ситуация существует, то отклонение от нее невыгодно самому игроку.

ТЕОРЕМА (Дж. Нэш). Всякая биматричная игра имеет хотя бы одну равновесную ситуацию (точку равновесия) в смешанных стратегиях.

Итак, равновесная ситуация существует. Но как ее найти?

Дляобоснования способа определения равновесной ситуации сошлемся на следующийтеоретический результат.

ТЕОРЕМА. Выполнение неравенств (2.7.3) равносильно выполнению неравенств

H_A(0, q*) £ H_A(р*, q*), H_B(р*, 0) £ H_B(р*, q*), (2.7.4)

H_A(1, q*) £ H_A(р*, q*), H_B(р*, 1) £ H_B(р*, q*).

Иными словами, для того чтобы убедиться, что пара (p*, q*)определяет равновесную ситуацию, достаточно проверить справед­ливость неравенств (2.7.2) только для двух чистых стратегий игрока А (р = 0 и р = 1) и для двух чистых стратегий игрока В (q = 0 и q = 1).

Пропуская промежуточные алгебраические выкладки, приходим к следующему результату:

Для того чтобы в биматричной игре пара (p*, q*)определяла равновесную ситуацию, необходимо и доста­точно одновременное выполнение следующих неравенств:

(p- 1)(Cq- a) ³ 0,

p (Cq- a) ³ 0,

(q- 1)(Dp- b)³0, (2.7.5)

q (Dp - b) ³ 0,

0 £ р £ 1, 0 £ q £ l,

где

С = a ₁₁ – a ₁₂ – a ₂₁ + a ₂₂, a = a ₂₂ – a ₁₂,

D = b ₁₁ – b ₁₂ – b ₂₁ + b ₂₂, b = b ₂₂ – b ₂₁,

Дата добавления: 2015-04-24