Условная сходимость несобственных интегралов

Интеграл называется условно сходящимся, если он сходится, а интеграл 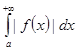расходится.

Покажем, что интеграл 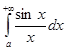условно сходится.

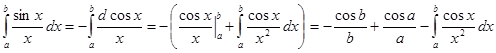
Перейдем к пределу при 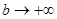. Интеграл в правой части равенства абсолютно сходится, обозначим его I.

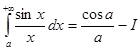. Поэтому интеграл 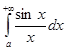сходится.

Покажем, что этот интеграл не сходится абсолютно. Справедливо неравенство . .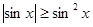

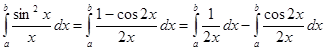Переходя к пределу при 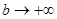, видим, что интеграл сходится (аналогично интегралу 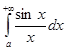), интеграл 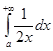расходится. Поэтому интеграл 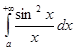расходится. Если бы он сходился, то складывая его с сходящимся интегралом 0.5 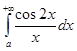, получили бы сходящийся интеграл (0.5 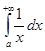), а этот интеграл расходится.

Используя неравенство 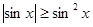и расходимость интеграла 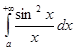, по первому признаку сравнения получаем расходимость интеграла 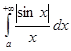. Следовательно, интеграл 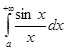условно сходится.

Лекции 9-10. Приложения определенного интеграла.

Приложение интеграла к физическим задачам основано на свойстве аддитивности интеграла по множеству. Поэтому с помощью интеграла могут вычисляться такие величины, которые сами аддитивны по множеству. Например, площадь фигуры равна сумме площадей ее частей Длина дуги, площадь поверхности, объем тела, масса тела обладают тем же свойством. Поэтому все эти величины можно вычислять с помощью определенного интеграла.

Можно использовать два метода решения задач: метод интегральных сумм и метод дифференциалов.

Метод интегральных сумм повторяет конструкцию определенного интеграла: строится разбиение, отмечаются точки, в них вычисляется функция, вычисляется интегральная сумма, производится предельный переход. В этом методе основная трудность – доказать, что в пределе получится именно то, что нужно в задаче.

Метод дифференциалов использует неопределенный интеграл и формулу Ньютона – Лейбница. Вычисляют дифференциал величины, которую надо определить, а затем, интегрируя этот дифференциал, по формуле Ньютона – Лейбница получают требуемую величину. В этом методе основная трудность – доказать, что вычислен именно дифференциал нужной величины, а не что-либо иное.

Дата добавления: 2015-04-24