Лекции 15–16. Линейные дифференциальные уравнения n –ого порядка с переменными коэффициентами

Линейное однородное дифференциальное уравнение n –ого порядка с переменными коэффициентами может быть записано в виде

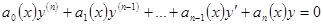
Линейное неоднородное дифференциальное уравнение n –ого порядка с переменными коэффициентами может быть записано в виде

.

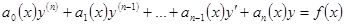Если коэффициенты и правая часть – непрерывные функции и 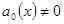, то условия теоремы Коши выполнены, решения однородного и неоднородного уравнений существуют и единственны.

Введем линейный дифференциальный оператор

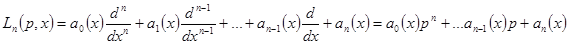Здесь обозначает оператор дифференцирования .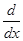

Тогда линейное однородное уравнение можно записать в виде 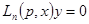, а линейное неоднородное – в виде .

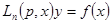Так как линеен, то

.

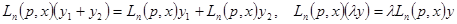Пользуясь линейностью оператора, легко доказать теоремы о свойствах решений однородного и неоднородного уравнений (ниже обозначено - решение однородного уравнения, - решение неоднородного уравнения).

Теоремы о свойствах решений.

a) сумма или разность решений однородного уравнения есть решение однородного уравнения,

b) разность решений неоднородного уравнения есть решение однородного уравнения,

c) сумма решений однородного и неоднородного уравнений есть решение неоднородного уравнения.

Докажем эти теоремы.

1)

2)

3) .

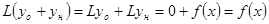Теорема. Решения линейного однородного уравнения с переменными коэффициентами образуют линейное пространство.

Доказательство. Так как сумма любых двух решений однородного уравнения и произведение любого решения на число вновь есть решения однородного уравнения, то операции сложения и умножения на число на множестве решений определены корректно (не выводят за множество решений).

Решения образуют аддитивную группу по сложению (абелев модуль). В самом деле, ассоциативность по сложению очевидна, 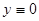(тривиальное решение) является решением однородного уравнения, для каждого решения 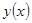противоположное решение 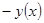тоже является решением. Следовательно, решения однородного уравнения – группа по сложению. Аддитивность решений очевидна, поэтому эта группа аддитивна. Справедливость четырех аксиом из восьми показана. Существует число «1», такое что 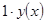- решение, справедлива ассоциативность по умножению на число 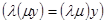. Это – две аксиомы относительно операции умножения на число. Наконец, справедливы две аксиомы дистрибутивности, связывающие операции сложения и умножения на число .

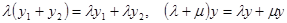Итак, налицо полный набор из восьми аксиом. Продумайте их еще раз подробнее дома.

Дата добавления: 2015-04-24