Метод Эйлера

Это простейший метод решения задачи Коши, позволяющий интегрировать дифференциальные уравнения первого порядка. Его точность невелика, но в некоторых случаях, например, в системах управления электроприводов, он применяется достаточно часто. На основе этого метода легче понять алгоритмы других, более эффективных методов.

Рассмотрим снова дифференциальное уравнение в форме Коши

y’ = f (t, y), (3.9)

удовлетворяющее начальному условию

y (t ₀) = y ₀. (3.10)

Численное решение задачи состоит в построении таблицы приближенных значений y ₁, y ₂, …., y_n решения уравнения (3.9) в точках t ₁, t ₂, …., t_n. Точки t ₁, t ₂, …., t_n - узлы сетки. Используем систему равноотстоящих узлов. Величина h - шаг сетки (шаг интегрирования).

Метод Эйлера основан на разложении y в ряд Тейлора в окрестности t ₀:

Если h мало, то члены, содержащие h во второй или более высоких степенях, являются малыми более высоких порядков и ими можно пренебречь. Тогда

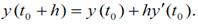
y' (t ₀) находим из дифференциального уравнения (3.9), подставив в него начальное условие (3.10). Таким образом можно получить приближенное значение зависимой переменной при малом смещении h от начальной точки. Этот процесс можно продолжить, используя соотношение

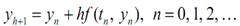
и делая сколь угодно много шагов.

Геометрический смысл метода Эйлера заключается в аппроксимации решения на отрезке [ t_n, t_{n +1}] отрезком касательной, проведенной к графику решения в точке t_n (рис. 3.3). Как видно из рис. 3.3, на каждом новом шаге приближенное решение переходит на другой член семейства решений. В результате накапливается ошибка дискретизации, которая линейно зависит от h, так как члены ряда Тейлора, содержащие h во второй и более высоких степенях, отбрасываются. Поэтому метод Эйлера имеет первый порядок точности.

Рис. 3.3 Геометрическая интерпретация метода Эйлера

Практическим следствием этого факта является ожидание того, что при уме-ньшении h приближенное решение будет все более точным и при стремлении h к нулю будет сходиться к точному решению с линейной скоростью по h; т.е. мы ожидаем, что при уменьшении шага h вдвое ошибка уменьшится в 2 раза. Очень медленная сходимость при уменьшении h характерна для методов первого порядка и служит препятствием для их широкого использования.

Дата добавления: 2015-04-24