
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Линейное дифференциальное уравнение 2-го порядка
|
|
|
|
Определение: Линейное дифференциальное уравнение (ДУ) второго порядка вида
 ,
,  (1)
(1)
называется неоднородным или неавтономным уравнением. Ему соответствует однородное или автономное д.у.
 (2)
(2)
Решение ищется в виде 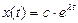 , уравнение
, уравнение
 (3)
(3)
называется характеристическим уравнением. Найдем решения (3)

Возможны три качественно различных случая

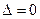 ,
, 
А) 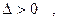
 действительные различные корни.
действительные различные корни.
Тогда 
 , поэтому если
, поэтому если  , то
, то  , если
, если 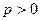 , то
, то 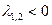
 тогда
тогда  .
.
Нулевое решение  - асимптотически устойчиво при
- асимптотически устойчиво при 
асимптотически неустойчиво при 
седловое при  .
.
Б) 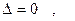
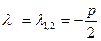 два равных корня.
два равных корня.
Тогда 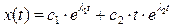 (5)
(5)

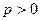 - решение
- решение  асимптотически устойчиво
асимптотически устойчиво

 - решение
- решение  асимптотически неустойчиво
асимптотически неустойчиво
Замечание при 
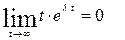 , т.к.
, т.к. 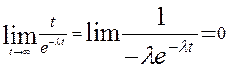 (правило Лапиталя)
(правило Лапиталя)
Результат при 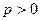
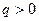

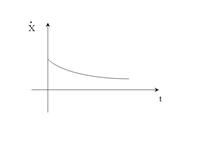
апериодический процесс, затухание.
Нас интересуют графики x(t), как функции времени t, и фазовые портреты, соответствующие всем рассмотренным случаям. И то, и другое зависит от параметров p и q. Для наглядности введем в рассмотрение плоскость параметров p и q. Граничному случаю, разделяющему разные случаи, отвечает равенство 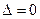 , которому на плоскости соответствует парабола
, которому на плоскости соответствует парабола
 . На рисунке приведена бифуркационная диаграмма и соответствующие разным областям фазовые портреты.Разбиение плоскости параметров p и q на области соответсвующим различными корням l1 и l2 характеристического уравнения: комплексные с отрицательными действительными частями(устойчивый фокус),3) комплексные с положительными действительными частями(неустойчивый фокус), 4) действительные отрицательные(устойчивый узел), 5) действительные положительные(неустойчивый узел) и
. На рисунке приведена бифуркационная диаграмма и соответствующие разным областям фазовые портреты.Разбиение плоскости параметров p и q на области соответсвующим различными корням l1 и l2 характеристического уравнения: комплексные с отрицательными действительными частями(устойчивый фокус),3) комплексные с положительными действительными частями(неустойчивый фокус), 4) действительные отрицательные(устойчивый узел), 5) действительные положительные(неустойчивый узел) и 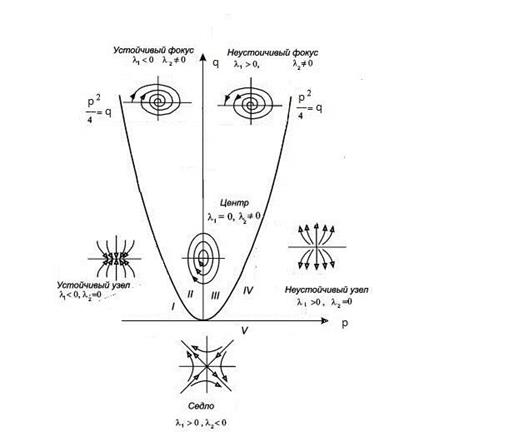 6) действительные разных знаков (седло)
6) действительные разных знаков (седло)
Ниже приведем фазовые портреты, соответствующие различным поведениям систем и состояниям равновесия, более подробно:
|
|
|
- устойчивый и неустойчивый фокус:

- устойчивый и неустойчивый узел:
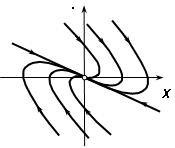
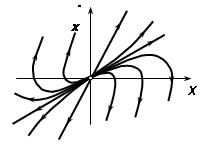
- седло:

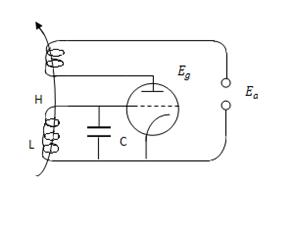
Напишем мат. модель для рассматриваемой электрической схемы Ia- анодный ток, Eд – напряжение на сетке, относительно катода q-заряд конденсатора. Пусть c, r, l, соответственно емкость конденсатора, сопротивление резистора, индукция катушки, а М- её коэффициент взаимоиндукции с нагрузкой в анодном контуре. Для колебательного контура состоящего из самоиндукции L, емкости C и сопротивления R имеем:

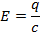

Вид зависимости анодного тока от напряжения на сетке трехэлектродной лампы
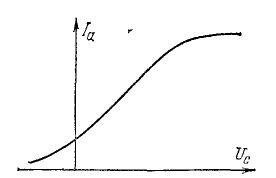
Примем, что Ia=α+βE-γE
При этом пренебрегаем самоиндукцией анодном контуре и принимаем, что:
L  +R
+R  +
+  =M(
=M( -
- 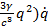
Или
 +
+ 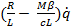 +
+  =0
=0
Это уравнение приводится к уравнению Ван дер Поля
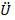 -2δ(1-α
-2δ(1-α  )
)  +ω2 U=0
+ω2 U=0
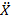 +λ(X2-1)
+λ(X2-1) 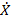 + ω2 X=0
+ ω2 X=0
2δ= 
α= 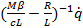 +
+ 
ω2= 
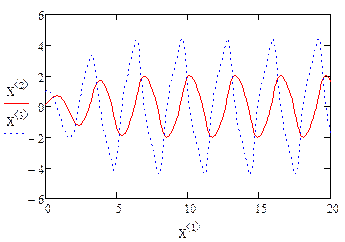
При этом предполагается, что δ>0;α >0; ω2 >0 При α=0 и очень малых u уравнение Ван дер Поля превращается в линейный осциллятор с отрицательным трением δ>0 при u2>1/ α
Коэффициент при 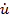 становится положительным и можно предполагать, что при этом колебания затухают.Таким образом состояние равновесия осциллятора Ван дер Поля не устойчиво и малые колебания нарастают, а очень большие колебания затухают и следовательно, между ними должно быть устойчивое периодическое движение
становится положительным и можно предполагать, что при этом колебания затухают.Таким образом состояние равновесия осциллятора Ван дер Поля не устойчиво и малые колебания нарастают, а очень большие колебания затухают и следовательно, между ними должно быть устойчивое периодическое движение

Компьютерное моделирование:

|
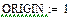
|

|

|

|

|
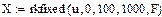
|

|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 953; Нарушение авторских прав?; Мы поможем в написании вашей работы!