Исследование биквадратного уравнения

Трехчленные уравнения, приводящиеся к квадратным уравнениям

Трехчленные уравнения

Й способ

Расположим в левой части слагаемые по убывающим степеням x, получим квадратное уравнение относительно x: .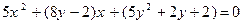

Это уравнение при действительных значениях y имеет действительные корни тогда и только тогда, когда его дискриминант неотрицателен, т. е.

.

Это неравенство после раскрытия скобок принимает вид 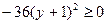. Последнее возможно лишь при y = -1, а тогда из уравнения следует, что x = 1.

Ответ: x = 1, y = -1.

Трехчленное уравнение вида 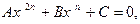где n > 2 - натуральное число, 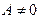, при помощи подстановки сводится к квадратному уравнению

.

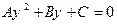Частным видом трехчленного уравнения является биквадратное уравнение

.

Преобразуем биквадратное уравнение к приведенному. Для этого разделим обе его части на A, зная, что 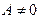, получим:

.

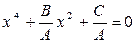Положим 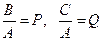, приходим к уравнению: .

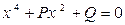Заменим 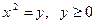, получим квадратное уравнение: .

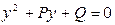Полученное квадратное уравнение, при D < 0, т. е. при не имеет действительных корней, а значит не будет иметь корней и исходное биквадратное уравнение.

Если D = 0, т. е. 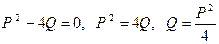, тогда квадратное уравнение имеет один действительный корень 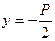, а биквадратное уравнение может:

а) имеет два равных по модулю, но противоположных по знаку корня - это будет в том случае, если полученный корень положительный, что произойдет при ;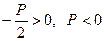

б) не имеет корней, если полученный корень отрицательный, что получится при P > 0;

в) иметь единственный корень, x = 0, если P = 0, но тогда и Q = 0.

Если D > 0, 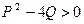, тогда квадратное уравнение имеет два различных действительных корня 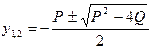, а биквадратное уравнение может:

а) не иметь действительных корней, если оба корня отрицательные, что произойдет при ;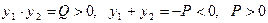

б) имеет два корня, если один из корней квадратного уравнения отрицателен, а другой - положителен, т. е. корн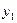и и 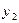- разных знаков, что произойдет при Q<0;

в) имеет три корня, если один из корней соответствующего квадратного уравнения равен нулю, а второй положителен, положим 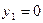, а 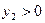, что произойдет при ;

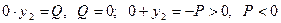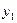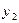г) имеет четыре корня, если оба корня и положительные, что произойдет при Q > 0 и P < 0.

Выводы

1. Биквадратное уравнение 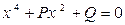не имеет действительных кор ней, если:

а) ; б) 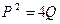и P > 0; в) 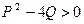, Q > 0 и P > 0.

2. Биквадратное уравнение имеет один действительный корень, если:

P = Q = 0.

3. Биквадратное уравнение имеет два действительных, равных по модулю, но противоположных по знаку, отличных от нуля корня, если:

а) 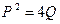и P < 0; б) 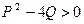и Q < 0.

4. Имеет четыре действительных, отличных от нуля, корня, если 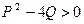, Q > 0 и P < 0.

Пример 1. Решить уравнение на множестве действительных чисел

.

Решение

Положим 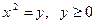, получим квадратное уравнение 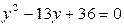, которое имеет два различных действительных корня: .

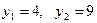Получим два уравнения:

(1) ; (2) .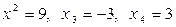

Ответ: , .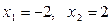

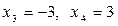Пример 2. При каком значении 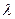равнение имеет два равных по модулю корня?

.

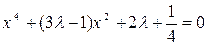Решение

Биквадратное уравнение имеет два действительных, равных по модулю, но противоположных по знаку, отличных от нуля корня, если:

а) 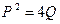и P < 0;б) 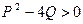и Q < 0.

Для данного уравнения: , .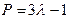

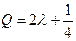а) Получим смешанную систему:

б) Из условий 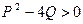и Q < 0 получим систему неравенств:

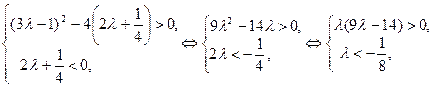
Рис. 56

Ответ: пр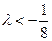и и 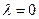, или можно записать так .

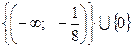Пример 3. При каких значениях параметра a уравнение имеет ровно три корня:

.

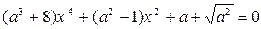Решение

Уравнение имеет три различных действительных корня, если P < 0 и Q = 0.

Преобразуем уравнение в приведенное, потребовав, чтобы . Это неравенство будет выполняться при .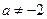

Получим приведенное уравнение: 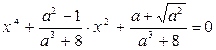, в котором .

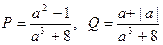Для этого уравнения получим смешанную систему:

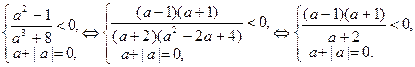
Последняя система распадается на совокупность двух систем:

(1)

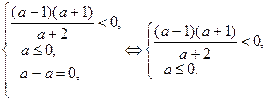
Эту систему решим методом промежутков:

Рис. 57

Получим результат: .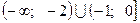

(2) 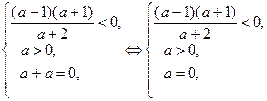система не имеет решений.

Осталось исследовать уравнение, при значении a = -2. Получим уравнение:

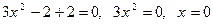. В этом случае, уравнение имеет только один корень, значит a = -2 не может удовлетворять условию задачи.

Ответ: .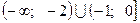

Пример 4. При каких значениях параметра a уравнение имеет ровно три корня:

.

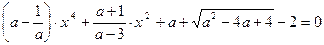Решение

Область допустимых значений параметра a: .

Преобразуем уравнение к приведенному, предположив при этом, что первый коэффициент не равен нулю: .

Получим уравнение .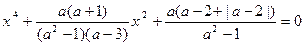

Поскольку 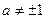, тогда уравнение примет вид:

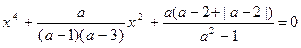, в котором ,

.

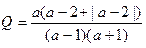Уравнение имеет три различных действительных корня, если P < 0 и Q = 0.

Получим смешанную систему

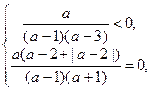поскольку 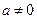, тогда система примет вид:

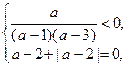которая распадается на две системы.

(1)

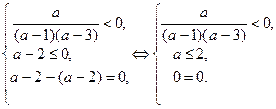
Рис. 58

Решением системы является объединение промежутков: .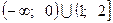

(2) 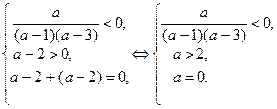система не имеет решений.

Исследуем уравнение при a = -1 и a = 1.

Если a = -1, уравнение примет вид: 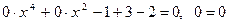- уравнение имеет бесконечное множество решений, значит a = -1 не удовлетворяет условию задачи.

Если a = 1, уравнение примет вид: 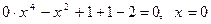- один корень, значит a = 1 не удовлетворяет условию задачи.

Ответ: .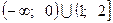

Задание 1

1. При каких значениях параметра a уравнение имеет единственный корень:

1) ;

2) .

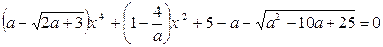2. При каких значениях параметра a уравнение имеет ровно три корня:

1) ;

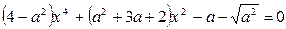2) .

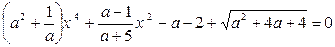Дата добавления: 2015-04-24