
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кубические уравнения с действительными коэффициентами
|
|
|
|
Решение кубических уравнений по формуле Кардано
Для любителей и знатоков
Мы познакомились с решением трехчленных кубических уравнений по формуле Кардано, затем решали уравнения, степени выше второй, используя различные частные методы. Но существует метод решения кубических уравнений с любыми комплексными коэффициентами по формуле, когда корни выражаются через коэффициенты уравнения.
Пусть дано кубическое уравнение (1) с любыми комплексными коэффициентами.
Решение
Заменим в уравнении (1) переменную x новым неизвестным y: получим уравнение:
Положим получим трехчленное кубическое уравнение вида: (2).
Мы уже знаем, что последнее уравнение решается по формуле Кардано:
(1')
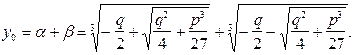 (2)
(2)
(3)
Если коэффициенты неполного кубического уравнения 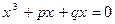 (4) - действительные числа, то основную роль играет знак выражения
(4) - действительные числа, то основную роль играет знак выражения 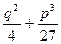 , стоящего в формуле Кардано под знаком квадратного корня.
, стоящего в формуле Кардано под знаком квадратного корня.
Знак этого выражения противоположен знаку выражения
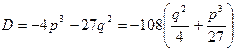 ,
,
которое называется дискриминантом неполного кубического уравнения. В дальнейших рассуждениях используется и указывается знак именно этого дискриминанта.
1. Пусть D < 0. В этом случае в формуле Кардано под знаком каждого из квадратных корней стоит положительное число, а поэтому под знаком каждого из кубических корней оказываются действительные числа. Кубический корень из действительного числа имеет одно действительное значение и два сопряженных комплексных корня. Пусть 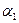 будет действительное значение корня
будет действительное значение корня  ; тогда значение
; тогда значение 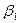 радикала
радикала 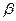 , соответствующее
, соответствующее 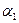 на основании формулы
на основании формулы 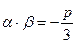 , также будет действительным ввиду действительности числа p.
, также будет действительным ввиду действительности числа p.
|
|
|
Таким образом, корень 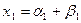 уравнения (4) оказывается действительным. Два других корня мы найдем, заменяя в формулах (3) корни из единицы
уравнения (4) оказывается действительным. Два других корня мы найдем, заменяя в формулах (3) корни из единицы 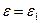 и
и 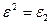 из выражения (5):
из выражения (5):
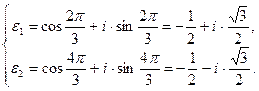 (5)
(5)
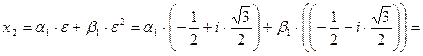
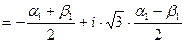 ,
,
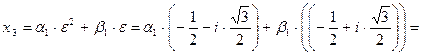
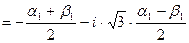 .
.
Эти два корня оказываются ввиду действительности чисел 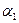 и
и 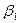 сопряженными комплексными числами, причём коэффициент при мнимой части отличен от нуля, так как
сопряженными комплексными числами, причём коэффициент при мнимой части отличен от нуля, так как 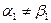 , - эти числа являются значениями различных кубических корней.
, - эти числа являются значениями различных кубических корней.
Таким образом, если D < 0, то уравнение (4) имеет один действительный и два сопряжённых комплексных корня.
2) Пусть D = 0. В этом случае
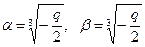 .
.
Пусть 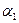 будет действительное значение радикала
будет действительное значение радикала  ; тогда
; тогда 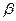 также будет, ввиду равенства
также будет, ввиду равенства 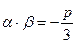 , действительным числом, причем
, действительным числом, причем 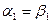 . Заменяя в формулах (3)
. Заменяя в формулах (3) 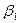 через
через 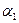 и используя очевидное равенство
и используя очевидное равенство  , мы получим:
, мы получим:
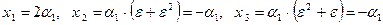 .
.
Таким образом, если D = 0, тo все корни уравнения (4) действительны, причем два из них равны между собой..
3) Пусть, наконец, D > 0. В этом случае в формуле Кардано под знаком квадратного корня стоит отрицательное действительное число, поэтому под знаками кубичных корней стоят сопряженные комплексные числа. Таким образом, все значения корней  и
и 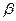 будут теперь комплексными числами. Среди корней уравнения (4) должен, однако, содержаться хотя бы один действительный. Пусть это будет корень
будут теперь комплексными числами. Среди корней уравнения (4) должен, однако, содержаться хотя бы один действительный. Пусть это будет корень
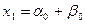 .
.
Так как действительны и сумма чисел 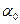 и
и 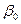 , и их произведение, равное
, и их произведение, равное 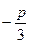 , то числа
, то числа 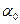 и
и 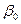 сопряжены между собой как корни квадратного уравнения с действительными коэффициентами. Но тогда сопряжены между собой и числа
сопряжены между собой как корни квадратного уравнения с действительными коэффициентами. Но тогда сопряжены между собой и числа 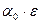 и
и 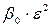 , а также числа
, а также числа 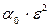 и
и 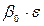 , откуда следует, что корни уравнения (4)
, откуда следует, что корни уравнения (4)
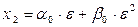 ,
, 
также будут действительными числами.
Мы получили, что все три корня уравнения (4) действительны, причем легко показать, что среди них нет равных. В самом деле, в противном случае выбор корня х1 можно было бы осуществить так, чтобы имело место равенство x2 = x3 откуда
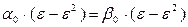 ,
,
т. е. 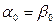 , что явно невозможно.
, что явно невозможно.
Таким образом, если D > 0, то уравнение (4) имеет три различных действительных корня.
|
|
|
Рассмотренный сейчас последний случай показывает, что практическое значение формулы Кардано весьма невелико. В самом деле, хотя при D > 0 все корни уравнения (4) с действительными коэффициентами являются действительными числами, однако разыскание их по формуле Кардано требует извлечения кубичных корней из комплексных чисел, что мы умеем делать лишь переходом к тригонометрической форме этих чисел. Поэтому запись корней с помощью корней теряет практическое значение. При помощи методов, выходящих за рамки этой главы, можно было бы доказать, что в рассматриваемом случае корни уравнения (4) вообще никаким способом не могут быть выражены через коэффициенты при помощи корней с действительными подкоренными выражениям и. Этот случай решения уравнения (4) называется неприводимым (не смешивать с неприводимостью многочленов!).
Пример 1. Решите уравнение по формуле Кардано
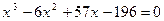 .
.
Решение
Положим 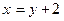 , получим
, получим 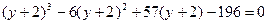 ,
,
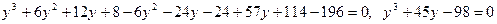 .
.
Здесь 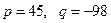 , поэтому
, поэтому
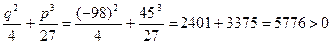 ,
,
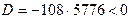 - уравнение имеет один действительный и два сопряжённых комплексных корня.
- уравнение имеет один действительный и два сопряжённых комплексных корня.
По формулам (1')
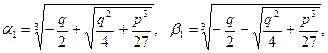
находим 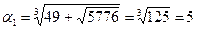 ,
, 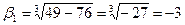 ,
, 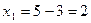 .
.
Два других корня найдём по формулам
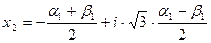 ,
, 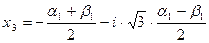
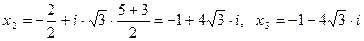
Ответ: 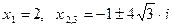 .
.
Пример 2. Решите уравнение по формуле Кардано
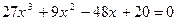 .
.
Решение
Преобразуем уравнение, разделив обе его части на коэффициент при 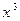 , т. е. на 27, получим уравнение:
, т. е. на 27, получим уравнение:  .
.
Положим  , получим
, получим 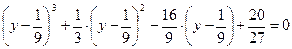 ,
,
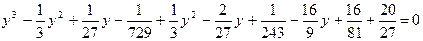 ,
,
 ,
, 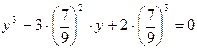 .
.
Здесь 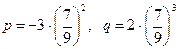 , поэтому
, поэтому
 ,
,
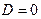 - уравнение имеет три действительных корня, причём два из них равны между собой.
- уравнение имеет три действительных корня, причём два из них равны между собой.
По формуле
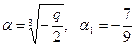 ,
,
находим 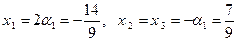 .
.
Ответ: 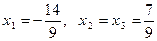 .
.
Пример 3. Решить уравнение, применяя формулу Кардано
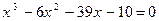 .
.
Решение
Подстановка 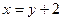 приводит это уравнение к виду
приводит это уравнение к виду
 ,
,
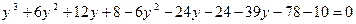 ,
, 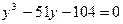 .
.
Здесь 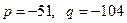 , поэтому
, поэтому
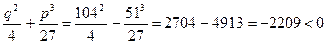 ,
,
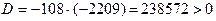 - уравнение имеет три различных действительных корня, но если оставаться в области действительных чисел, формула Кардано к этому уравнению не применима, хотя его корнями являются действительные числа
- уравнение имеет три различных действительных корня, но если оставаться в области действительных чисел, формула Кардано к этому уравнению не применима, хотя его корнями являются действительные числа 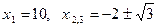 .
.
Ответ: 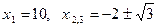 .
.
Задание 1
Решите по формуле Кардано уравнения
1.  . 2.
. 2. 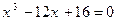 . 3.
. 3. 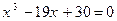 .
.
4. 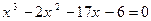 . 5.
. 5. 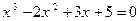 . 6.
. 6. 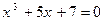 .
.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 2802; Нарушение авторских прав?; Мы поможем в написании вашей работы!