
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные цели и задачи динамических расчетов, механических систем с учетом упругости звеньев. 1 страница
|
|
|
|
1
Тираж 250 экз. Заказ.
**
Редакционно-издательский отдел ОмГУПСа
Типография ОмГУПСа
*
644046, г. Омск, пр. Маркса, 35
Учет упругих свойств звеньев при построении динамических моделей механизмов позволяет решать новый класс задач, без которых немыслимо построение скоростных современных машинных агрегатов.
ЦЕЛИ:
- устранение (режимных) аварийных резонансных режимов (из-за резонансных режимов аварийность в технике на 1-ом месте);
- обеспечение норм. условий эксплуатации механизмов – ограничение уровня колебаний, воспроизведение с заданной точностью требуемых кинематических зависимостей (в США в 40-х г.г. прошлого века);
- виброизоляция машин и приборов;
- ограничение уровня колебаний для защиты человека (оператора) – самые опасные частоты 5-7Гц (сек-1), до 200Гц вызывают виброболезнь;
- использование вибраций для осуществления технологических и транспортных операций.
При решении задач динамики механизмов с упругими звеньями мы сталкиваемся со всеми видами механических колебаний.
2 СТРУКТУРА ДИНАМИЧЕСКОГО РАСЧЕТА.
Эксперимент
↓
Физ. объект → ДМ1 → ММ1 → Решение → Анализ → Задача
ДМ2 ММ2 оптимизации
….. ……
ДМk MMk
Физ.объект (машина, станок, мост и т.д.)
1 этап Составление динамической модели объекта
ДМ-идеализированное отображение рассматриваемой МС (станок, его узел), используемой при её теоретическом исследовании и инженерных расчетах и составленная с учетом поставленной динамической задачи.
Исходная схема ременной передачи

расчетная динамическая модель ременной передачи
I1 - момент инерции массы (кг*м);
Ck - жесткость при кручении.
2 этап Составление математической модели по динамической модели физического
|
|
|
объекта
ММ – система дифференциальных или интегральных уравнений, с помощью которых описывается модель.
3 этап Решение уравнений аналитическое, получается достоверная качественная картина процесса или решение численными методами с применением ЭВМ.
4 этап Анализ решения и вывод о соответствии физического объекта к требованиям.
5 этап Задача оптимизационного динамического синтеза механизма является наиболее важной и актуальной современной проблемой динамики машин.
Применительно к колебательным системам машин - это задача снижения виброактивности механизмов. На каждом этапе динамического расчета принимается допущения (ограничения) – не учитываются трения в кин. парах и т.д. Поэтому желателен на каждом этапе эксперимент.

Современное машиностроение характеризуется тенденцией значительного повышения производительности машин (увеличение объема технологических операций, сокращение времени переходных процессов, повышение надежности и точности, повышение рабочих нагрузок, экономичности). Эффективное проектирование при таких противоречивых требованиях невозможно без тщательного анализа движения в машине с учетом упругости звеньев и всех основных силовых факторов, это входит в задачу динамики машин, которая является фундаментальной основой их проектирования и анализа.
Основное допущение ТММ о недеформируемости звеньев механизмов, их динамических моделей и отсутствие зазоров в кинематических парах. Такие динамические модели называются кинетостатическими, а результаты расчетов идеальными.
Кинетостатическая механическая модель двухступенчатого зубчатого редуктора
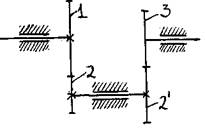
В общем виде связь между входом и выходом подобных механизмов определяется уравнением:

 где
где  - координата выхода звеньев,
- координата выхода звеньев,
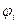 - координата входа звеньев,
- координата входа звеньев,
|
|
|
П – функция положения.
z1 для нашего случая:
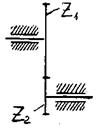
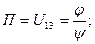
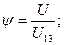
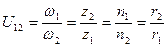 - передаточное отношение
- передаточное отношение
U13=U12 · U23 - передаточное число
В подобных кинетостатических механизмах все звенья абсолютно твердые, гибкие звенья не растяжимы, в кинемат. парах отсутствуют зазоры, т.к. все звенья выполнены геометрически точно.
Практика эксплуатации машин. агрегатов свидетельствует о том, что при современном рабочем объеме и нагрузках данное допущение применимо лишь в первом приближении, а чаще совсем не допустимо, это относится и к деревообрабатывающему оборудованию, т.к. оно отличается высоким частотным уровнем технологических нагрузок. Деревообрабатывающие машины, как и любые другие, представляют собой упругие механические системы.
При воздействии на такую механическую систему нагрузок, особенно переменных из-за наличия неуравновешенных движущихся масс и податливых участков конструкций в ней возникают динамические нагрузки (упругие перемещения) - механические колебания, т.е. механические колебания возникают из-за упругости звеньев и неточности изготовления, наличие зазоров в зацеплении. Вследствие механических колебаний в машинах возникают погрешности в работе механизмов, увеличивается износ деталей, снижается надежность машин, т.к. возникают усталостные разрушения в материале в результате переменных нагрузок, что может привести к аварии.
Таким образом, необходимость представления механических систем как упругой системы очевидна. Навыки по динамическому расчету механизмов с учетом упругости звеньев, правильная оценка воздействия мех. системы – необходимое качество современного инженера.
ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИИ ПРИ МАЛЫХ КОЛЕБАНИЯХ.
При рассмотрении колебательного движения предполагается, что система обладает одним положением устойчивого равновесия. В противном случае колебания вообще не происходят. Условие устойчивости положения равновесия консервативной механической системы сформулирована в системе Лагранжа-Дирихле:»Если для материальной системы, находящейся в консервативном поле силовом и подчиненным голономным идеальным и стационарным связям потенциальная энергия имеет в положении равновесия min, то это положение равновесия является устойчивым».
|
|
|
В общем случае потенциальная энергия – функция обобщенных координат и времени.
В механизмах потенциальная энергия, участвующая в колебательном процессе, формируется в основном за счет упругих деформаций. Рассмотрим механическую систему, подчиненную голономным стационарным связям с п -степенями свободы, т.е. заданы q1, q2,…qn.
Потенциальная энергия системы: V(q1, q2,…qn) – это механическая система имеет некоторое положение статического равновесия, принимаемая за начало отсчета (нулевой уровень), в этом положении равновесия координаты системы равны 0: q1=0, q2=0,…qn=0, тогда потенциальная энергия на нулевом уровне равна 0, V0=0. Кроме того, исходя из принципа свободных перемещений, обобщенная сила, соответствующая любой координате, Qi=0, а следовательно:  - частная производная по
- частная производная по  .
.
Предполагая, что функция V характеризуется потенциальной энергией в окрестности положения равновесия непрерывно и дифференцируемо, разложим её в ряд Маклорена:
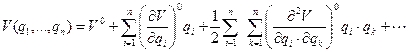 (50)
(50)
Первым ненулевым членом в разложении 3-е слагаемое – квадратичная форма записи потенциальной энергии консервативной мех. системы: 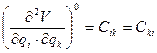 (51)
(51)
Обозначим выражение в скобках как постоянные коэффициенты, квазиупругие, обладающие свойством симметрии Cik=Cki, тогда 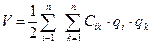 (52) - выражение потенциальной энергии в квадратичной форме записи. С – квазиупругие коэффициенты в упругой системе, обладающая свойством симметрии, тогда квадратичная форма записи кинетической энергии:
(52) - выражение потенциальной энергии в квадратичной форме записи. С – квазиупругие коэффициенты в упругой системе, обладающая свойством симметрии, тогда квадратичная форма записи кинетической энергии: 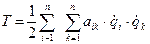 (53)
(53)
aik=aki – инерционныекоэффициенты, обладающие свойством симметрии;
 - обобщенные скорости.
- обобщенные скорости.
В развернутом виде зависимость (53) примет следующий вид:
1) Н=1 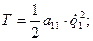
(54) 2) Н=2 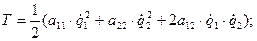
3) Н=3 
Выражение (52),записанное в раскрытом виде, полностью совпадает с зависимостями (54). Если коэффициент aik заменить на сik, а обобщенные скорости обобщенными координатами …
При рассмотрении малых колебаний квадратичные формы потенциальной и кинетической энергии консервативной системы можно записать в матричной форме:
 (55)
(55)
 (55) Т - знак транспонирования
(55) Т - знак транспонирования
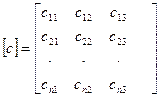 - матрица жесткости
- матрица жесткости
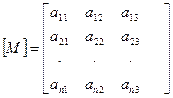 - матрица инерции
- матрица инерции
|
|
|
{q} – матрица – столбец обобщенных координат
ПРАКТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ИНЕРЦИОННЫХ И КВАЗИУПРУГИХ
КОЭФФИЦИЕНТОВ.
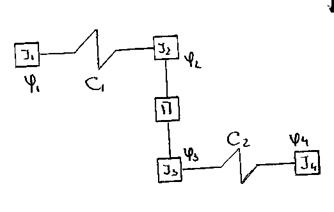
Дана исходная схема привода:

1) Составим динамическую модель:
I1 – момент инерции ротора
I2 –момент инерции зубчатого колеса
I3 – момент инерции зубчатого колеса
I4 – момент инерции выход. звена
П – функция положения
Считаем зубчатое зацепление идеальным: П = U 23
φ – углы поворота сосредоточенных масс
2) Определим число степеней свободы (метод засечек)
N =3
3) Выбор обобщенных координат
q1=φ1 - угол поворота ротора
q2=φ2-φ1=>φ2=q1+q2;
φ3=U32·φ2=U32·(q1+q2);
φ4=φ3+q3=U32·(q1+q2)+ q3;
т.к.число степеней N=3, для определения коэффициента см.уравнение (54).
3) Запишем выражение кинетической и потенциальной энергии
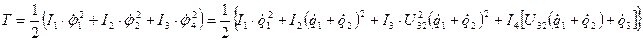
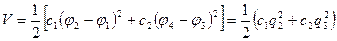 ;
;
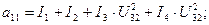









Пример: Построение математической модели системы с N=2 на базе уравнения Лагранжа второго рода в обобщенных координатах с записью в квадратичной форме.
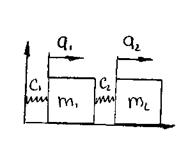
1) 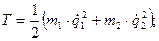
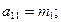
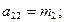


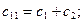
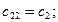


 ;
;
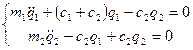
УРАВНЕНИЕ ЛАГРАНЖА ВТОРОГО РОДА В ОБОБЩЕННЫХ КООРДИНАТАХ
c записью потенциальной и кинетической энергии в квадратичной форме
Теоретической основой большей части динамических расчетов мех. систем с конечным числом степеней свободы служит уравнение Лагранжа в обобщенных координатах.
При их составлении полагали связи, наложенные на систему, идеальные, т.е. уравнения не содержат реакций связей и входящие в них величины, определяющие движение системы (обобщенные координаты и их производные по времени) непосредственно связаны с заданными обобщенными силами.
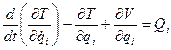 (56) i =1, 2, 3,…, n
(56) i =1, 2, 3,…, n
Qi – внешние обобщенные неконсервативные силы
 (57)
(57)
для исследования свободных колебаний консервативной системы правая часть равна 0.
Рассмотрим случай представления в виде квадратичных форм T и V, при этом в выражениях (56) и (57) второе слагаемое равно 0, т.к. в выражение кинетической энергии (53) обобщенные координаты в явном виде не входят, следовательно, для малых колебаний уравнение Лагранжа в обобщенных координатах имеет вид:
 (58)
(58)
Выразим слагаемые уравнения (58) с учетом квадратичных форм записи T и V
(см. уравнение 54).
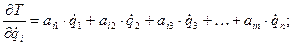


Таким образом, после подстановки (52 и 54) в уравнение (58) получим систему п -диффе-ренциальных уравнений второго порядка, где п – число степеней свободы исследуемой механической системы.
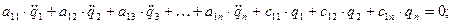

…………………………………………………………………………. (59)
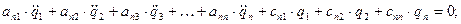
Видна закономерность в индексах инерционных и квазиупругих коэффициентов:
первый индекс отвечает номеру уравнения,
второй индекс – номеру обобщенного ускорения или обобщенной координаты, при которой стоит данный коэффициент.
Систему (59) без труда можно воспроизвести, не прибегая к подстановке кинетической и потенциальной энергии, что позволяет автоматизировать составление математической модели, при большом числе п более удобна матричная форма записи:
10 КЛАССИФИКАЦИЯ МЕХАНИЧЕСКИХ КОЛЕБАНИЙ:
| По виду возмущений | По виду деформаций | ДМ | ММ |
| -свободное колебание -вынужденное колебание -параметрические колебания -автоколебания | -продольное колебание -крутильное колебание -изгибное колебание | -модель с распред. параметрами Н = ∞ (число степеней свободы) -модель с сосредоточ. параметрами Н ≠ ∞ | -линейное колебание -нелинейное колебание |
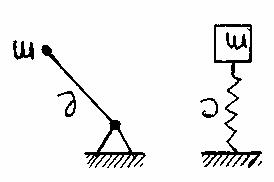
Свободное колебание:
с – жесткость пружины,
е – длина нити
Свободное колебание совершается за счет начальных условий, т.е. происходит за счет возмущений в начальный момент времени, после этого система предоставлена сама себе, т.е. совершает свободное колебание с собственной частотой колебания.
Начальных условий может быть два:
- начальное отклонение системы от положения устойчивого равновесия (потенциальная энергия);
- начальная скорость (кинетическая энергия).
Вынужденное колебание происходит под действием переменной во времени вынуждающей силы явной функции времени.

Параметрические колебания происходят за счет изменения параметров самой системы во времени, т.е. параметры системы функции времени.
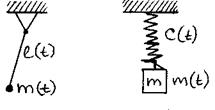
Автоколебания – установившийся колебательный процесс, возникающий при источнике энергии неколебательной природы.
Линейные колебания – описывают линейными диф.уравнениями.

Линейная система – имеет абсолютно жесткую массу, линейную пружину (подчиняются закону Гука), вязкий линейный демпфер, и все это сосредоточенные параметры.
Нелинейные колебания – решаются численными методами, приближенно, рассматривается поведение линейных систем.
11 I. ПЕРИОДИЧЕСКОЕ ДВИЖЕНИЕ.
Простое гармоническое движение механических систем.

Если колебательное движение системы периодическое, то система повторяет свое движение (координаты, скорость и ускорение) через равные промежутки времени.
Время, затраченное на повтор одного цикла – период Т - T (c);
Частота периодического движения - величина, обратная периоду, число колебаний в единицу времени - ν (c-1) [Гц]; 
Движение, которое не повторяется в равные промежутки времени, наз. апериодическим.
Простое гармоническое движение (гармоническое колебание) – это периодическое движение, возвратно-поступательное, описывается круговыми функциями (sin, cos) совершается под действием силы пропорциональной смещению и направленной противоположно ему.

А – амплитуда колебаний, наибольшее по модулю отклонение тела от положения равновесия
Геометрическая модель гармонических колебаний.
Рассмотрим простое гармоническое движение линейной динамической модели с одной степенью свободы, с наложенными ограничениями (допущениями):
- силы трения в системе не учитываются, т.е. нет диссипации энергии (рассеяния энергии), т.е. система консервативная;
- движение строго вдоль оси х.
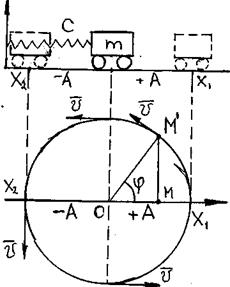
Приведем систему в состояние свободного колебания путем начального смещения массы M в точку х1
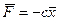 , F = cx,
, F = cx,
где с – коэффициент пропорциональности (жесткость пружины), [Н/м].
При этом работа полная механическая, совершаемая системой, равна:
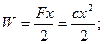
Т.к. система линейная, сила упругости и величина деформации пружины относятся друг к другу в соответствии с законом Гука.
 - зависимость линейная,
- зависимость линейная,
т.е. полная работа равна площади заштрихованных фигур, т.к. в положении с1 система обладает максимальной потенциальной энергией (Vmax), т.е. Vmax = W;
то 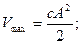 х=А;
х=А;
Рассмотрим движение сосредоточенной массы m как движение точки по диаметру окружности радиусом R.
При колебательном движении т. М из положения х1 в х2 и обратно проекция т.М совершает вращательное движение с угловой скоростью p, которую мы называем собственной круговой частотой колебаний
φ = p · t; 2 π = р · Т;  (1)
(1)
т.к. проекция окружной скорости на ось х V максимальна в положении устойчивого равновесия т. М, а в крайних точках х1 и х2 равна 0, следовательно максимальной кинетической энергией система обладает при прохождении сосредоточенной массы m в положение устойчивого равновесия (т.О). Таким образом, происходит трансформация одной энергии в другую, т.е. при гармоничном колебании происходит переток потенциальной энергии в кинетическую и обратно:
Vmax = Tmax = W, а т.к.  , то
, то 
V = ω · r; V = p ·A (в нашем случае), тогда 
Подставим в выражение для А выражение для равенства энергии

 ;
;  (2)!
(2)!
Свободные колебания системы совершаются с собственной частотой колебаний.
Собственная частота – единственная наиболее важная характеристика механической колебательной системы, т.к. все системы стремятся совершать колебания на собственной частоте, При расчете собственной частоты и периода свободных колебаний при отсутствии в системе специальных демпфирующих устройств силами сопротивления (трения) можно пренебречь, т.е. считать систему консервативной.
Для колебательного движения решаются 2 задачи, как и для любого вида движения:
1 – основная задача механики – определение координаты в любой момент времени,
2 – т.к. речь идет о периодических колебаниях, то вычисляем период.
12 .СВОБОДНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
Тимошенко «Колебание в инженерном деле»
Если статически нагруженную систему (упругую: типа груз на прутике, балка на двух опорах) вывести из состояния равновесия каким-либо образом, то внутренние силы и изгибающие моменты в деформированном состоянии уже не будут находиться в равновесии с внешними нагрузками – возникнут колебания.
Рассмотрим поведение системы, задав одну обособленную координату, т.е. систему с одной степенью свободы, наложив на нее те же ограничения (см. предыдущий раздел).

По 2-му закону Ньютона запишем уравнение нашей системы:
 преобразуем и получим:
преобразуем и получим:
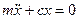 / т
/ т
 (3)
(3)
дифференциальное уравнение второго порядка в свободных колебаниях системы (однородное дифференциальное уравнение)
Частные решения:
х = c1 · cos pt, где с – постоянная интегрирования
х = c2 · sin pt
Решение в общем виде:
х = c1 · cos pt+ c2 · sin pt (4)
Для определения с1 и с2 рассмотрим начальный момент времени t=0;
Q имеет перемещение хо и имеет начальную скорость  .
.
Подставим t=0 в уравнение (4) и получим: с1 = хо;
взяли 1-ую производную и, подставив t=0, получим:
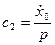 ;
;
таким образом, уравнение (4) перепишется:
 (5)
(5)
Данное уравнение описывает колебательное движение груза массой m.
Уравнение (5) имеет геометрическую интерпретацию как вращение двух векторов на фазовой плоскости х.

хо cos pt – проекция хо на ось х
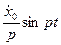 - проекция амплитуды А2 на ось х
- проекция амплитуды А2 на ось х
А – сумма векторная векторов хо и 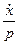
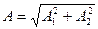
А cos(pt-α) – проекция А на ось х
 (6)
(6)


Вывод:
 - однородное дифференциальное уравнение 2-го порядка свободных колебаний (гармонических колебаний) одномассовой системы линейной с одной степенью свободы.
- однородное дифференциальное уравнение 2-го порядка свободных колебаний (гармонических колебаний) одномассовой системы линейной с одной степенью свободы.
Решение уравнения в общем виде:

Решение в эквивалентном виде:
х = А cos(pt-α),
где:  , (7)
, (7)
α - угол рассогласования (фазовый угол) ,  , (8)
, (8)
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 1258; Нарушение авторских прав?; Мы поможем в написании вашей работы!