Рождение предельного цикла. Бифуркация Андронова-Хопфа

Существование предельных циклов возможно лишь в системе типа (8.1), правые части которой представлены нелинейными функциями.

На бифуркационной диаграмме 4.11 мы видели, что при пересечении оси абсцисс происходит смена устойчивости фокуса. Нулевым значениям действительной части характеристических чисел (ляпуновских показателей) соответствует особая точка типа центр. В нелинейной системе, где возникает неустойчивый фокус, при этом возможно рождение предельного цикла. Такой переход легко проследить в «модельной» системе:

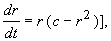
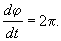^(8.3)

Схематически возникновение предельного цикла в системе (8.3) изображено на фазопараметрической диаграмме на рис. 8.6.

Рис. 8.6. Закритическая (суперкритическая) бифуркация Андронова-Хопфа. Мягкое возбуждение. При с >0 возникают автоколебания, амплитуда которых растет с увеличением с.

Выполнению условия Re l_1,2 = 0, причем Im l_1,2 ¹ 0, соответствует бифуркация Андронова–Хопфа или бифуркация рождения (исчезновения) предельного цикла. Бифуркация впервые была исследована А.А. Андроновым для случая N = 2 и обобщена Е. Хопфом на системы с произвольной размерностью. (Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. М., Наука, 1981; Hopf E., 1942)

Существуют два типа бифуркации Андронова–Хопфа. Только что мы рассмотрели суперкритическую бифуркацию (мягкое возбуждение автоколебаний). Возможна также субкритическая бифуркация (жесткое возбуждение автоколебаний). В этом случае при бифуркационном значении параметра устойчивый фокус теряет устойчивость из-за «влипания» в него неустойчивого предельного цикла (рис. 8.7). Фокус становится неустойчивым, а аттрактором при этом может стать предельный цикл большой амплитуды.

Рис. 8.7. Докритическая (субкритическая) бифуркация Андронова – Хопфа. Жесткое возбуждение автоколебаний. «Локальные события» при изменении параметра при переходе через бифуркационное значение: устойчивый фокус и неустойчивый предельный цикл пунктир, (а) при уменьшении параметра с переходятв центр (б),а затем в неустойчивый фокус (в). Внешний большой устойчивый предельный цикл находится за пределами локальной системы, в которой происходит бифуркация.

Устойчивый фокус (неустойчивый предельный цикл)

Центр

Неустойчивый фокус (устойчивый предельный цикл)

«Модельной» системой (см. лекция 6), описывающей рождение предельного цикла при жестком возбуждении, является система:

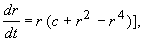
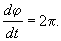^(8.4)

Приравняв правую часть первого уравнения нулю, получим стационарные значения r:

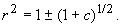
Ветвь r = 0 устойчива при c < 0 и неустойчива при c > 0.

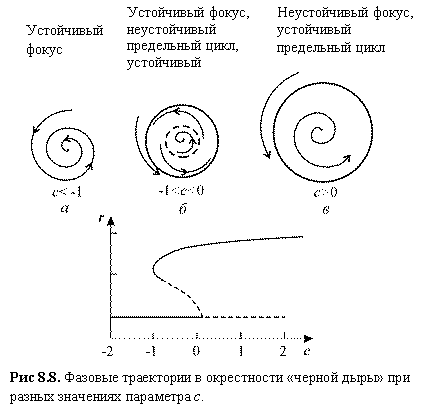
Рис 8.8. Фазовые траектории в окрестности «черной дыры» при разных значениях параметра c.

Устойчивый фокус

Устойчивый фокус, неустойчивый предельный цикл, устойчивый предельный цикл

Неустойчивый фокус, устойчивый предельный цикл

При с > –1 стационарное решение - устойчивый предельный цикл.

При –1 < с < 0 стационарное решение - неустойчивый предельный цикл.

Рассмотрим, что произойдет, если двигаться по параметру с, начиная с отрицательных значений (Рис.8.8). Первоначально имеется единственное устойчивое стационарное состояние r = 0, колебаний нет. При c > –1 существует также устойчивый предельный цикл, но система не покидает своего устойчивого стационарного состояния. Однако после того как с становится положительным, стационарное состояние становится неустойчивым, и происходит резкий скачок к устойчивому предельному циклу. В системе начинаются колебания сразу большой амплитуды. Если двигаться от положительных значений с к отрицательным, колебания большой амплитуды сохраняются до тех пор, пока с не станет меньше –1, а затем внезапно исчезнут. Таким образом при –1 < с < 0 могут существовать два различных типа поведения. Какой из них реализуется, зависит от предыстории системы. Такой феномен называется эффектом гистерезиса.

При увеличении параметра с и его переходе через ноль скачком возникают устойчивые автоколебания конечной амплитуды и частоты. Для промежуточных значений параметра с существуют два типа устойчивого поведения (два аттрактора) - устойчивое стационарное состояние и устойчивый предельный цикл.

Винфри (Winfree A.T.)назвал области, в которых возможны два режима: устойчивая точка покоя и предельный цикл, ­- черной дырой (рис. 8.8 б). В этой области параметров можно так приложить возмущение к колебательной системе, что она попадет в область притяжения точки покоя, что приведет к прекращению колебаний. В частности, это показано для уравнений Ходжкина–Хаксли, моделирующих проведение нервного импульса (см. ниже).

Брюсселятор. Простейшим классическим примером существования автоколебаний в системе химических реакций является тримолекулярная модель «Брюсселятор», предложенная в Брюсселе Пригожиным и Лефевром (1965). Основной целью при изучении этой модели было установление качественных типов поведения, совместимых с фундаментальными законами химической и биологической кинетики.

В этом смысле блюсселятор играет роль базовой модели, такую же как гармонический осциллятор в физике, или модели Вольтерра в динамике популяций. Во 2-й части лекций мы остановимся на пространственно‑временных свойствах распределенной системы, локальным элементом которой является брюсселятор. Здесь мы рассмотрим свойства брюсселятора как автоколебательной системы.

Брюсселятор содержит простейшую реализацию кубической нелинейности посредством химической реакции

2 X + Y ® 3 X (8.5)

Хотя тримолекулярная стадия в химической кинетике не столь распространена, как бимолекулярные процессы, выражения для скорости ряда биохимических реакций в определенных случаях можно свести к кубическому виду. В качестве примера приведем следующую последовательность ферментативных реакций:

X + E ® EX

EX + Y ® XY

EXY + X ® EX ₂ Y

Здесь предполагается что фермент E имеет по крайней мере три каталитических центра, способных одновременно фиксировать две молекулы X и одну молекулу Y. Если образующиеся комплексы распадаются с достаточно большой скоростью, а ферменты присутствуют в небольших количествах, легко показать, что всю последовательность реакций можно свести к одной стадии, дающей нелинейный член типа X ² Y в выражении для скорости реакции.

Брюсселятор представляет собой следующую схему гипотетических химических реакций:

A X

2 X + Y 3 X  

B + X Y + C  

X R

Здесь А, В — исходные вещества, C, R — продукты, X, Y — промежуточные вещества.

Пусть конечные продукты С и R немедленно удаляются из реакционного пространства. Это означает, что обратные константы k _-3 = k _-4 = 0. Если субстрат A находится в избытке, k _-1 = 0. Предположим также, что k _-2 = 0. Значения остальных констант положим равными единице. Тогда схема реакций 9.2 (в случае точечной системы) описывается системой уравнений:

,

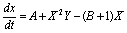(8.6)

Модель (8.5) имеет одну особую точку с координатами:

. (8.7)

Исследуем стационарное решение (8.6) на устойчивость по методу Ляпунова. Введем переменные, характеризующие отклонения от особой точки:

.

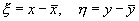Линеаризованная система имеет вид:

,

.

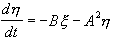Характеристическое уравнение

или

l ² + (A ² + 1 - B) l + A ² = 0

имеет корни:

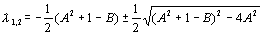. (8.7)

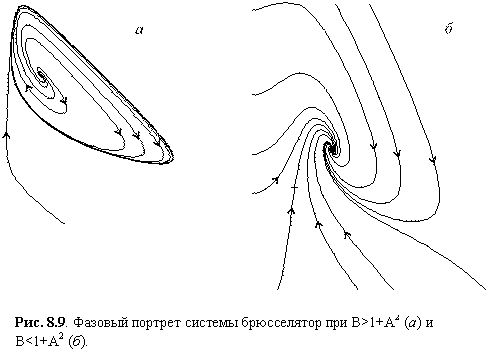
Напомним, что особая точка является устойчивой, если действительные части корней характеристического уравнения отрицательны. Из выражения (8.7) видно, что при B < 1 + A ² особая точка (8.6) устойчива. Если же B > 1 + A ² особая точка становится неустойчивой, и у системы (8.5) появляется устойчивый предельный цикл. Значение B = 1 + A ² является бифуркационным. Если величина B лишь немного превосходит бифуркационный порог, автоколебания в системе носят квазигармонический характер. Таким образом, брюсселятор при выполнении условия

Рис. 8.9. Фазовый портрет системы брюсселятор при B>1+A² (а) и B<1+A² (б).

B > 1 + A ² (8.8)

является автоколебательной системой. Фазовый портрет брюсселятора при разных значениях параметров изображен на рис. 8.9

Здесь мы приведем краткий обзор нескольких «успешных» моделей колебательных биологических процессов. Более подробно некоторые колебательные процессы будут рассмотрены в лекциях 9, 11, 12.

Дата добавления: 2015-04-25