Собственные колебания стержневых конструкций

Динамические характеристики элементов конструкций РЭА, приводимых к системам с распределенными параметрами

Расчет колебаний несущих конструкций радиоэлектронных систем – сложная задача. На практике реальные конструкции и их элементы заменяют упрощенными идеализированными физическими моделями – стержнями и пластинами. Для таких моделей достаточно достоверно могут быть определены низшие собственные частоты и формы колебаний.

Стержневые конструкции применяют в качестве силовых элементов конструкций РЭА как в виде отдельных стержней (валы, кронштейны), так и в виде более сложных устройств (рамы, каркасы). Стержневые конструкции могут совершать различные колебания.

Рассмотрим продольные колебания. Продольные колебания стержня описываются уравнением [5]

Здесь 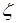= – смещение текущего сечения стержня вдоль оси ;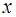

– модуль упругости;

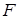– площадь поперечного сечения стержня;

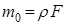– масса единицы длины стержня;

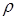– плотность материала.

Для стержня постоянного сечения это уравнение будет иметь вид

(1)

где 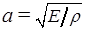имеет смысл скорости распространения продольных волн в стержне.

Уравнение (1) получено по модели плоских сечений, согласно которой любые точки, лежащие в плоскости, перпендикулярной к оси стержня, имеют одинаковые перемещения. Оно выражает условие равенства сил инерции и сил упругости, действующих на элементарный участок стержня.

Решение уравнения (1) можно представить в виде

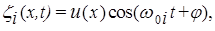(2)

где – собственная или амплитудная функция, определяющая форму колебаний;

– -я собственная частота ( = 1, 2, 3,…).

Подстановка решения (2) в уравнение (1) приводит к дифференциальному уравнению для амплитудной функции

, (3)

где

Общее решение уравнения (3) имеет вид

(4)

Таким образом, форма колебаний зависит от постоянных интегрирования А, В и волнового числа которое является функцией собственной частоты. Для их определения необходимо рассмотреть граничные условия, зависящие от способа от способа крепления концов стержня.

Рассмотрим определение собственных частот и форм колебаний на примере стержня с одним жестко заделанным и вторым свободным концом (рис. 5).

Рисунок 5 – Форма продольных колебаний консольного стержня

Согласно граничным условиям при x = 0 u = 0;

при x = l u ´ = 0 (u ´ = du/dx).

Используя эти выражения и решение (4), получаем:

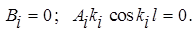
Одно из слогаемых исключается, а из второго при условии А ≠ 0 получаем частотное уравнение

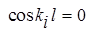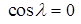или . (5)

Из решения этого уравнения получаем формулу для определения собственных частот

. (6)

Таким образом, стержень обладает бесконечным числом собственных частот. Низшая частота (частота основного тона колебаний)

. (6а)

Подставляя значения частот из (6) в решение (4), определим собственные формы колебаний, соответствующие различным i:

. (7)

Аналогично определяются собственные частоты и формы колебаний при других граничных условиях.

Рассмотрим изгибные колебания стержней (рис. 6). Жесткость стержня на изгиб обычно бывает значительно ниже жесткости на растяжение, поэтому расчет изгибных колебаний стержней представляет для практики значительный интерес.

При расчете предполагают, что упругая ось стержня совпадает с линией центра масс поперечных сечений (рис. 6) и при колебаниях все точки стержня смещаются перпендикулярно первоначальному (прямолинейному) направлению оси. Все поперечные сечения при этом остаются плоскими.

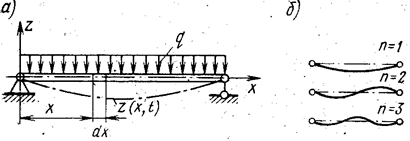Рисунок 6 – Изгибные колебания стержня:

а – схема нагружения; б – форма колебаний

В расчете учитываются только силы инерции, действующие в направлении оси z, и силы упругости, препятствующие деформации изгиба стержня. В этом случае уравнение движения стержня имеет вид:

(8)

Здесь – момент инерции сечения относительно оси, перпендикулярной плоскости изгиба;

– жесткость стержня при изгибе, характеризующая его способность сопротивляться искривлению оси.

Уравнение (8) выражает равенство действующих на элемент стержня равномерно распределенных нагрузок от сил инерции и упругости. Для его решения функция z (x, t) может быть представлена в виде

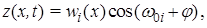(9)

где амплитудная функция, характеризующая отклонение точек стержня от положения равновесия на i- той резонансной частоте.

Функция называется собственной формой колебаний стержня и зависит от способа закрепления концов стержня, т.е. от граничных условий.

Подстановка (9) в (8) дает

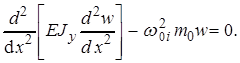(10)

В общем случае ρ, Е, F, J могут быть переменными по длине стержня, и тогда уравнение (10) не имеет точного решения. Для случая, когда эти значения постоянны, уравнение (10) примет вид (символ аргумента у функции w опущен)

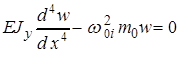. (11)

Общее решение уравнения состоит из сумм четырех частных решения. Оно может быть представлено в виде

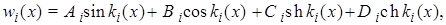(12)

где 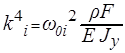. (13)

Таким образом, форма колебаний зависит от постоянных интегрирования и параметра , т.е. от от частоты . Для определения постоянных интегрирования должны быть рассмотрены граничные условия, зависящие от способа закрепления концов стержня [6]

В частности, для приведенного выше случая стержня с шарнирно закрепленными (опертыми) концами (рис. 6) граничные условия будут:

при x = 0 w = 0

при x = l w = 0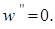

Частотное уравнение для данного способа закрепления стержня будет

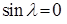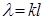(), (14)

а его корни будет 1, 2, …).

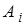Уравнением формы колебаний для данного частного случая будет уравнение синусоиды , амплитуда которой представляет собой максимальный прогиб стержня.

Значение корня частотного уравнения (14) определяет форму колебаний колебаний (в данном случае - число полуволн синусоидальной линии изгиба, укладывающихся на длине стержня) и соответствующую собственную частоту. Эта частота находится из (13) подстановкой в него корней частотного уравнения (14):

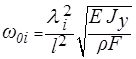(15)

Для консольно закрепленного стержня (рис. 7) граничные условия будут:

при x = 0 w =

при x = l w = 0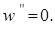

Рисунок 7 – Формы изгибных колебаний консольного стержня

Для стержня, оба конца которого жестко заделаны, граничные условия будут:

w = при x = 0 и x = l.

Анализ (15) показывает, что стержень имеет бесконечное число собственных форм колебаний и соответствующее им число собственных частот, при этом частоты всех тонов быстро возрастают. Из (15) также видно, что любая собственная частота стержня сильно зависит от его длины (обратно пропорционально квадрату длины) и в меньшей степени от размеров и формы поперечного сечения и свойств материала. Это дает возможность конструктору корректировать частотные характеристики разрабатываемой конструкции.

Дата добавления: 2015-04-25