Понятие растрового алгоритма. Понятие связности. Основные требования, предъявляемые к растровым алгоритмам

Так как в подавляющем большинстве графические устройства являют­ся растровыми, то есть представляют изображение в виде прямоуголь­ной матрицы пикселов (растра), то, возникает необходимость в растровых алгоритмах.

Хотя большинство графических библиотек содержат внутри себя достаточное количество простейших растровых алгоритмов, таких, как:

• переведение идеального объекта (отрезка, окружности и др.) в их растровые образы;

• обработка растровых изображений.

Достаточно важным понятием для растровой сетки является связ­ность - возможность соединения двух пикселов растровой линией, то есть последовательным набором пикселей. При этом возникает вопрос, когда пикселы (х₁,у₁)и (х₂,y₂) можно считать соседними.

Вводится два понятия связности:

4-связность, когда пикселы считаются соседними, если либо их х-координаты, либо у-координаты отличаются на единицу, то есть

½x1-x2½+ ½y1-y2½£1,

8-связность, когда пикселы считаются соседними, если их х- и у-координаты отличаются не более чем на единицу, то есть

½x1-x2½£1, ½y1-y2½£1,

Понятие 4-связности является более сильным, чем 8-связность: любые два 4-связных пиксела являются и 8-связными, но не наоборот.

т.к. понятие линии базируется на понятии связанности, то естественным образом возникает понятие 4- и 8-связных линий. Поэтому когда идет речь о растровом представлении, например, отрезка, то следует ясно понимать, о каком именно представлении идет речь. При этом нужно иметь в виду, что растровое представление объекта не является единственным и возможны различные способы построения.

25. Растровое представление отрезка: постановка задачи, простейший алгоритм, алгоритм ЦДА.

"дискретная плоскость" – множество всех точек с целочисленными координатами на обычной плоскости. Дискретную плоскость часто называют целочисленной решеткой. Нельзя провести непрерывный отрезок прямой линии из одной точки экрана в другую. Можно только подсветить ближайшие к прямой пикселы. Процесс определения пикселов, наилучшим образом аппроксимирующих заданный отрезок, называется разложением отрезка в растр.

Отрезки должны удовлетворять следующим требованиям:

1. Отрезки должны выглядеть прямыми, начинаться и заканчиваться в заданных точках.

2. Яркость вдоль отрезка должна быть постоянной и не зависеть от длины и наклона.

3. Алгоритмы рисования должны быть простыми, т.е. отрезок “рисоваться” должен быстро.

При достаточно высоком разрешении дисплея можно получить приемлемую аппроксимацию прямой линии.

Следует отметить, что постоянная яркость будет у горизонтальных, вертикальных отрезков и под углом 45⁰, причем у отрезков под углом 45⁰ яркость будет меньше чем у вертикальных и горизонтальных отрезков.

Рассмотрим задачу построения растрового изображения отрезка, соединяющего точки (x1, y1) и (x2, y2). Для простоты будем считать, что 0£y2-y1£x2-x1. Тогда отрезок описывается следующим уравнением:

или у = kx+b.

Основной недостаток алгоритма - использование вещественных вычислений для работы на целочисленной решетке.

Другим простейшим алгоритмом разложения отрезка в растр является алгоритм, построенный по методу цифрового дифференциального анализатора (ЦДА).

Данный алгоритм пригоден для проведения отрезков во всех квадрантах декартовой системы координат.

1) Осуществляется аппроксимация длины отрезка (float len)

2) Полагаем большее из приращений Dy или Dx равным единице растра

3) Округляем величины, а не отбрасываем дробную часть

4) Начало основного цикла

i=1;

while (i<= Len)

{ PutPixel (Int (x), Int (y), Color);

x = x + Dx;

y = y + Dy;

i = i + 1;

}

Недостатки алгоритма разложения отрезка в растр, основанного на методе ЦДА:

1) Использует вещественную арифметику, что приводит к значительным затратам вычислительных ресурсов.

2) Может быть активизирован пиксел, стоящий за концом отрезка, и если рисуется ломаная, то данный пиксел будет высвечиваться 2 раза.

3) Результат работы алгоритма зависит от ориентации отрезка, т.е. точность на концевых точках отрезка ухудшается.

26. Растровое представление отрезка: постановка задачи, алгоритм Брезенхейма.

Процесс определения пикселов, наилучшим образом аппроксимирующих заданный отрезок, называется разложением отрезка в растр.

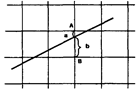Идея алгоритма состоит в том, что в процессе построения отрезка одна из координат - либо “х”, либо “y” (в зависимости от углового коэффициента) - изменяется на единицу. Изменение другой координаты (либо на нуль, либо на единицу) зависит от расстояния между “теоретическим” положением отрезка и ближайшими координатами сетки (такое расстояние в алгоритме называется “ошибкой”).

При построении растрового изображения отрезка всегда выбирается ближайший по вертикали пиксел. При этом из двух точек А и В выбирается та, которая ближе к исходной прямой (в данном случае выбирается точка А, так

как а < b).

При совмещении начала координат с одним из концов отрезка, имеем три возможные оси симметрии, и достаточно рассмотреть половину одного квадранта, например ту, для которой dx >= dy >= 0.

Уравнение прямой, описывающее отрезок:

представляет собой функцию ошибок, которая должна быть минимизирована по абсолютной величине в процессе генерирования. Оно становится равным нулю, когда точка находится на прямой.

Пусть E = y*dx - x*dy. (1)

Если за исходную точку принять начало координат, то достаточно двух элементарных движений, чтобы с их помощью перемещаться вдоль отрезка.

Движение A: увеличение x

x = x + 1; в результате согласно (1) ошибка уменьшается на величину dy:

E = E - dy;

Движение B: увеличение x и y

x = x + 1;

y = y + 1;

приводит в соответствии с (1) к возрастанию E на величину (dx - dy), имеющую положительное значение в рассматриваемой половине квадранта:

E = E + dx - dy;

исходя из этих соображений, построен итерационный алгоритм минимизации ошибки, при котором на каждом шаге выбирается соответствующее движение:

Этот алгоритм имеет два недостатка:

1. первое движение выбирается произвольно

2. ошибка изменяется от dx-dy до -dy и случайным образом большинство точек может расположиться выше или ниже истинного отрезка.

Обе проблемы отпадают, если центрировать функцию ошибки относительно нуля, начиная с величины (dy -dx/2):

E = dy - dx/2.

27. Растровое представление отрезка: построение сглаженной линии (метод Флойда-Стейнберга, модификация алгоритма Брезенхейма, сглаживание всей сцены).

Основной причиной лестничного эффекта является то, что отрезок или ребро какой-либо фигуры непрерывны для того, чтобы соответствовать дискретным пикселам экрана дисплея.

При наличии нескольких интенсивностей, т. е. полутонов серого или оттенков цвета, внешний вид ребра или отрезка может быть улучшен размыванием краев. Простой метод состоит в том, чтобы устанавливать интенсивность пиксела на ребре пропорционально площади части пиксела, находящейся внутри многоугольника.

В результате простой модификации алгоритма Брезенхейма можно получить аппроксимацию площади части пиксела, находящейся внутри многоугольника. Эту аппроксимацию можно использовать для модуляции интенсивности. При пересечении пиксела и отрезка с тангенсом угла наклона m (0 <= m <= 1) может быть задействован либо один, либо два пиксела. Если пересекается только один пиксел, то площадь правее и ниже отрезка равна у_i+ m/2.Если же надо рассмотреть два пиксела, то площадь нижнего пиксела составляет 1 - (1 - y_i)²/2m, а верхнего - (y_i-1+m)²/2m. Суммарная площадь для двух пикселов равна у_i + m /2.

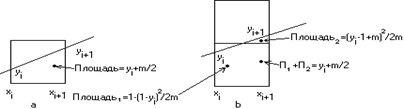
Алгоритм Брезенхейма, учитывающий площадь части пиксела для устранения ступенчатости.

Если к ошибке в исходном алгоритме Брезенхейма добавить величину w = 1 - m, т.е. ввести преобразование e' = e + w, то 0<=e'<=1. Теперь ошибка е' - это мера площади той части пиксела, которая находится внутри многоугольника, т. е. у_i+m/2. В связи с этими модификациями начальное значение ошибки равно 1/2, поэтому для первого пиксела алгоритм, приводившийся на первом рисунке, всегда будет выдавать значение интенсивности, равное половине максимальной. Более реалистичное значение для первого пиксела дает перемещение оператора активирования пиксела на другое место. Более того, можно получить непосредственно значение интенсивности, а не десятичную дробь от ее максимума с помощью умножения на максимальное число доступных уровней интенсивности I следующих величин: тангенса угла наклона (m), весового коэффициента (w) и ошибки е'.

28. Растровое представление окружности: постановка задачи, простой алгоритм, алгоритм Брезенхейма.

Из геометрии мы знаем, что окружность с центром в точке (xc,yc) и радиусом r, задается параметрически с помощью системы уравнений:

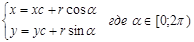
Отсюда не сложно получить алгоритм генерации окружности:

1. Полагаем А=0.

2. Если А больше либо равно 2p, то окружность отрисована.

3. Вычислим x=Trunc(xc+r*cos(A)), y=Trunc(yc+r*sin(A))

4. Screen[x,y]=Color

5. Увеличим A на d и перейдем к шагу 2.

В данном алгоритме d подбираем в зависимости от радиуса окружности и разрешающей способности устройства вывода. Основная причина, по которой использование данного алгоритма нецелесообразно – очень низкая скорость работы, связанная с использованием вещественных чисел, и тем более вычислением тригонометрических функций.

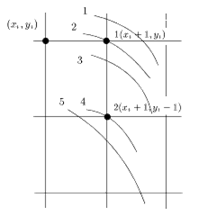
Если точка (x,y) лежит на окружности с центром в точке (0,0), то и точка (x,-y), так же лежит на этой окружности. Последнее утверждение можно развить, а именно: если точка (x,y) лежит на окружности с центром в точке (0,0), то и точки (x,-y);(-x,-y);(-x,y);(y,x),(y,-x);(-y,-x);(-y,x), так же лежат на этой окружности. Координата x увеличивается на единицу на каждом шаге. Так же координата y либо уменьшается на единицу, либо остается без изменений. Нужно выбрать, куда переходить из точки (x_i,y_i) либо в точку (x_i+1,y_i), либо в точку (x_i+1,y_i-1). Для того, чтобы осуществить выбор рассмотрим две невязки:

dⁱ₁=(x_i+1)²+y_i²-r²

dⁱ₂=(x_i+1)²+(y_i-1)²-r²

А так же будем следить за их суммой:

dⁱ=dⁱ₁+dⁱ₂

Рассмотрим несколько вариантов расположения "вещественной" окружности относительно "целых" точек:

Случай 1. dⁱ₁ < 0, dⁱ₂ < 0, и следовательно dⁱ < 0.

Случай 2. dⁱ₁= 0, dⁱ₂ < 0, и следовательно dⁱ < 0.

Случай 3. dⁱ₁ > 0, dⁱ₂ < 0, и следовательно имеем два варианта для dⁱ:

Случай 3.1. |dⁱ₁| < |dⁱ₂| и следовательно dⁱ < 0.

Случай 3.2. |dⁱ₁| > |dⁱ₂| и следовательно dⁱ > 0.

Случай 4. dⁱ₁ > 0, dⁱ₂=0, и следовательно dⁱ > 0:

Случай 5. dⁱ₁ > 0, dⁱ₂ > 0, и следовательно dⁱ > 0:

В случае, если dⁱ < 0 надо активировать точку (x_i+1,y_i), а в случае, если dⁱ > 0 надо активировать точку (x_i+1,y_i-1). dⁱ=dⁱ₁+dⁱ₂=(x_i+1)²+y_i²-r²+(x_i+1)²+(y_i-1)²-r²=2x_i²+2y_i²+4x_i-2y_i+3-2r²

Теперь получим выражение dⁱ⁺¹ через dⁱ .

dⁱ⁺¹=2x_i+1²+2y_i+1²+4x_i+1-2y_i+1+3-2r²=dⁱ+4(x_i-y_i)+10

Осталось получить значение d¹ в начальной точке (x₁=0,y₁=r):

d¹=3-2r

Если x > y, то выходим.

1. Screen[x+xc,y+yc]:=Color;

2. Screen[x+xc,-y+yc]:=Color;

3. Screen[-x+xc,y+yc]:=Color;

4. Screen[-x+xc,-y+yc]:=Color;

5. Screen[y+xc,x+yc]:=Color;

6. Screen[y+xc,-x+yc]:=Color;

7. Screen[-y+xc,x+yc]:=Color;

8. Screen[-y+xc,-x+yc]:=Color;

Если d < 0, то d:=d+4*x+6, переходим на Шаг 13

d:=d+4(x-y)+10; y:=y-1;

Дата добавления: 2015-03-29