Решение задач методом наложения

Задача 1.2.1. В электрической цепи рис. 1.2.1 с тремя источниками энергии определить все токи в ветвях, воспользовавшись методом наложения.

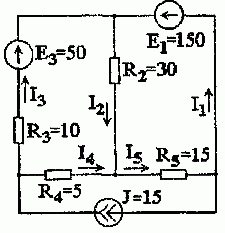
Рис. 1.2.1

Решение

1. Выполним расчет цепи при воздействии источника ЭДС E ₁, полагая E ₃ = 0, J = 0. Источники считаем идеальными, поэтому внутренние сопротивления ЭДС равны нулю, а источника тока – бесконечности. С учетом этого изобразим расчетную схему (рис. 1.2.2).

Рис. 1.2.2

Определение токов в полученной схеме будем вести, пользуясь методом эквивалентных преобразований:

R ′ Э = R 5 + R 2 ⋅ (R 3 + R 4) R 2 + (R 3 + R 4) =15+ 30⋅ (10+5) 30+ (10+5) =25  Ом; I ′ 1 = E 1 R ′ Э = 15025 =6  A;    I ′ 5 = I ′ 1 =6  A; I ′ 2 = I ′ 1 ⋅ R 3 + R 4 R 2 + (R 3 + R 4) =6⋅ 10+5 30+ (10+5) =6  A; I ′ 3 = I ′ 1 ⋅ R2 R 2 + (R 3 + R 4) =6⋅ 30 30+ (10+5) =4  A;    I ′ 3 = I ′ 4 =4  A.

2. Расчет электрической цепи при воздействии ЭДС источника Е ₃ выполним, полагая Е ₁ = 0, J = 0(рис. 1.2.3).

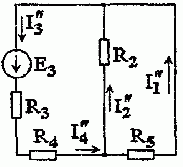
Рис. 1.2.3

В соответствии с рис. 1.2.3 имеем:

R ″ Э = R 3 + R 4 + R 2 ⋅ R 5 R 2 + R 5 =10+5+ 30⋅15 30+15 =25  Ом; I ″ 3 = E 3 R ″ Э = 50 25 =2  A;    I ″ 4 = I ″3 =2  A; I ″ 2 = I ″ 4 ⋅ R 5 R 2 + R 5 =2⋅ 15 15+30 =0,66  A; I ″ 5 = I ″ 4 ⋅ R 2 R 2 + R 5 =2⋅ 30 15+30 =1,33  A;   I ″ 1 = I ″ 5 =1,33  A.

3. Расчет электрической цепи при действии источника тока выполним, полагая E ₁ = 0, Е ₂ = 0 (рис. 12.4).

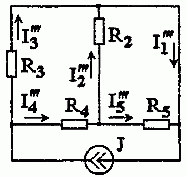
Рис. 1.2.4

В соответствии с рис. 1.2.4 имеем:

R ''' Э = R 4 + R 2 ⋅ R 5 R 2 + R 5 =5+ 30⋅15 30+15 =15  Ом.

Находим токи в параллельных ветвях:

I ''' 3 =J⋅ R ''' Э R ''' Э + R 3 =15⋅ 15 15+10 =9  A; I ''' 4 =J⋅ R 3 R ''' Э + R 3 =15⋅ 10 15+10 =6  A; I ''' 2 = I ''' 4 ⋅ R 5 R2 + R 5 =6⋅ 15 15+30 =2  A; I ''' 5 = I ''' 4 ⋅ R 2 R 2 + R 5 =6⋅ 30 15+30 =4  A.

Ток I ''' рассчитываем по первому закону Кирхгофа:

I ''' 1 + I ''' 5 −J=0;    I ''' 1 =J− I ''' 5 =15−4=11  A.

4. В соответствии с принятыми направлениями токов в исходной схеме определим их значения по методу наложения как алгебраическую сумму частичных токов всех промежуточных расчетных схем:

I 1 = I ′ 1 + I ″ 1 − I ''' 1 =6+1,33−11=−3,67  A; I 2 = I ′ 2 − I ″ 2 − I ''' 2 =2−0,66−2=−0,66  A; I 3 =− I ′ 3 − I ″ 3+ I ''' 3 =−4−2+9=3  A; I 4 = I ′ 4 + I ″ 4 + I ''' 4 =4+2+6=12  A; I 5 = I ′ 5 + I ″ 5 + I ''' 5 =6+1,33+4=11,33  A.

Правильность решения задачи проверяем по первому закону Кирхгофа:

−J+ I 3 + I 4 =0;   −15+3+12=0; − I 2 − I 4 + I 5 =0;  − (−0,66)−12+11,33=0.

Токи I ₁ и I ₂ получились отрицательными, т.е. их истинное направление в схеме противоположно принятому положительному направлению.

3 Метод контурных токов

.3 Метод контурных токов

В методе контурных токов за основные неизвестные величины принимают контурные токи, которые замыкаются только по независимым контурам (главным контурам). Контурные токи находят, решая систему уравнений, составленную по второму закону Кирхгофа для каждого контура. По найденным контурным токам определяют токи ветвей схемы.

Алгоритмом метода контурных токов:

1. Задаются направлением токов ветвей и обозначают их на схеме.

2. Определяют независимые контуры и их нумеруют. При наличии в схеме источников тока независимые контуры, для которых составляются уравнения метода контурных токов, можно определить, если мысленно удалить источники тока.

3. Выбирают направление контурных токов (целесообразно в одну сторону) и составляют уравнения по методу контурных токов, обходя каждый контур в направлении его контурного тока. Контурный ток, проходящий через источник тока, известен и равен току источника тока(через источник тока проходит только один контурный ток!).

4. Полученную систему алгебраических уравнений решают относительно неизвестных контурных токов.

5. Искомые токи по методу контурных токов находят как алгебраическую сумму контурных токов, проходящих по данной ветви. Токи в ветвях связи равны контурным токам.

Дата добавления: 2015-05-06